Przebieg ćwiczenia :

1.Ustalenie natężenia

2. Ustawienie temperatury na termostacie

3. Zmierzenie napięcia

4. Zmierzenie rezystancji próbki

Opracowanie wyników

Obliczenie niepewności uzyskanych wyników pomiarowych

ΔI = k ∙z /100 = 1,5 ∙ 5 mA /100 = 0,075 [mA] = 0,075 ∙ 10^{- 3} [A]

ΔU = 1 ∙ 10^{- 3} [V]

ΔT = 1 [K]

1. Korzystając z prawa Ohma, wyznaczenie rezystancji próbki metalowej

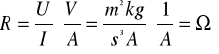
Prąd przepływający przez próbkę powinien być ustalony i wynosił średnio I=0,64 [mA]. Wyniki Obliczeń przedstawia tablica 1.

Tablica 1. Rezystancja próbki metalowej

Temperatura termostatu [°C]	Temperatura termostatu [K]	U [mv]	Rm [Ω]
20,6	293,6	66,3	103,6
22,6	295,6	67,0	104,7
24,6	297,6	67,7	105,8
26,6	299,6	67,8	105,9
28,6	301,6	68,1	106,4
30,6	303,6	68,3	106,7
32,6	305,6	68,4	106,9
34,6	307,6	68,6	107,2
36,6	309,6	69,0	107,8
38,6	311,6	69,3	108,3

Obliczenie niepewności wyznaczonych wartości rezystancji

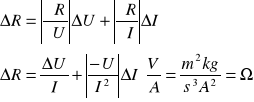
Tablica 2. Niepewności wyznaczenie wartości rezystancji próbki metalowej

Temperatura termostatu [K]	U [mv]	U[V]	Rm [Ω]	ΔRm [Ω]
293,6	66,3	0,066	104	14
295,6	67,0	0,067	105	14
297,6	67,7	0,068	106	14
299,6	67,8	0,068	106	14
301,6	68,1	0,068	106	14
303,6	68,3	0,068	107	14
305,6	68,4	0,068	107	14
307,6	68,6	0,069	107	15
309,6	69,0	0,069	108	15
311,6	69,3	0,069	108	15

2. Sporządzenie wykresu zależności temperaturowej rezystancji próbki metalowej i półprzewodnikowej od temperatury R=f(T) z zaznaczeniem niepewności wyznaczonych wielkości.

Poniższa tablica zawiera dane do wykreślenia wykresu dla próbki półprzewodnikowej

Tablica 3. Wartości rezystancji próbki półprzewodnikowej w zależności od temperatury

Temperatura termostatu [K]	Rp [Ω]	Rm [Ω]
293,6	1458	103,6
295,6	1424	104,7
297,6	1368	105,8
299,6	1353	105,9
301,6	1328	106,4
303,6	1297	106,7
305,6	1263	106,9
307,6	1222	107,2
309,6	1180	107,8
311,6	1135	108,3

Temperatura termostatu [K]	1/T *10^-3[K]	Rp [Ω]	LnR[Ω]
293,6	3,41	1458	7,28
295,6	3,38	1424	7,26
297,6	3,36	1368	7,22
299,6	3,34	1353	7,21
301,6	3,32	1328	7,19
303,6	3,29	1297	7,17
305,6	3,27	1263	7,14
307,6	3,25	1222	7,11
309,6	3,23	1180	7,07
311,6	3,21	1135	7,03

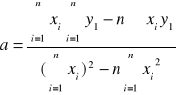
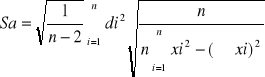
=0,23

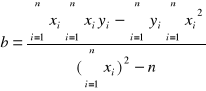
=0,021

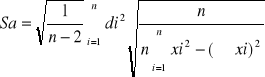
=38,3

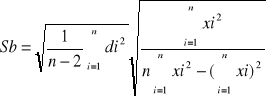
=6,2

Prosta aproksymująca wykres R = f(T)ma postać:

R = ( 0,23 T + 38,29 ) [Ω]

gdzie

a = ( 0,225+/- 0,021 ) [Ω/K]

b = ( 38,3+/- 6,2 ) [Ω]

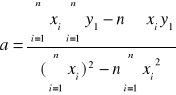
=0,225

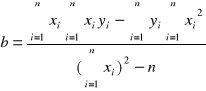
=0,021

=-3,23

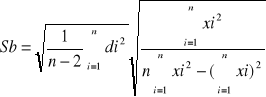
=0,23

Prosta aproksymująca wykres ln(R) = f(1/T)ma postać:

Ln(R) = ( 0,225/T - 0,021 ) [-]

gdzie

a = ( 0,225 +/- 0,021 ) [K]

b = ( -3,23+/- 0,23 ) [-]

Wyznaczam parametr α dla prostej R = ( 0,23 T + 38,29 ) [Ω]

=(1/101,08 )*0,23=2,28 *10^-3

gdzie T₀ = 0 [⁰C] =273 [⁰K] a więc R₀ = 273a + b=101,08

natomiast

Niepewność:

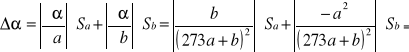
=0,16*10^-3

α= (101,1+/- 0,2) [1/Ω]

Wyznaczam wartość i niepewność energii aktywacji badanego półprzewodnika.

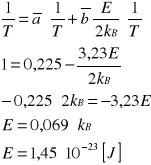
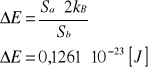
• Wnioski :

• Celem ćwiczenia było zbadanie zależności temperaturowej przewodnictwa elektrycznego dla metali i półprzewodników

• Energia aktywacji wyniosła 38 eV

• Opór zależy wprost proporcjonalnie od temperatury

Politechnika Śląska w Katowicach

SPRAWOZDANIE

Badanie zależności temperaturowej przewodnictwa elektrycznego metali i półprzewodników.

Grupa ZIP21

Sekcja 10:

Bartczak Tomasz Straszak Bartosz

---