Opracowanie wyników:
Obliczenie dla promieniowania tła średniej liczby zliczeń It licznika Geigera-Mullera w jednostce czasu.
Liczbę zliczeń It [imp/min] obliczamy ze wzoru:
![]()
gdzie:
N- liczba zliczeń licznika zarejestrowana podczas pomiaru
t- czas pomiaru
N- 117 [imp]
t- 600[s] = 10 [min]
![]()
Obliczona średnia wartość liczby zliczeń tła na jednostkę czasu wynosi: ![]()
![]()
Dokładność pomiaru określamy z warunku:
![]()
- warunek nie spełniony, dokładność nie mieści się w granicy 5%
It=(11,700±0,092)[imp/min]
Średnia wartość i odchylenie standardowe obliczone ze wzorów:
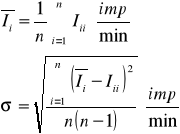
t - 60[s] = 1[min]
![]()
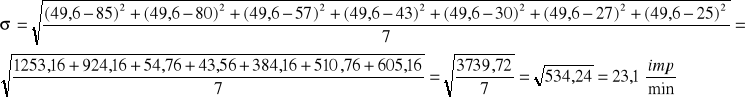
![]()
![]()
Obliczenie masy absorbenta na jednostkę powierzchni:
Wykorzystujemy wzór:
![]()
gdzie:
ρ- 8,92[g/cm3] - gęstość miedzi
x- grubość blaszki
Wyniki obliczeń przedstawia tabela:
x [cm] |
ρx[mg/cm2] |
|
0,000 |
0,00 |
|
0,007 |
62,4 |
|
0,015 |
133,8 |
|
0,020 |
178,4 |
|
0,028 |
249,8 |
|
0,034 |
303,3 |
|
0,041 |
365,7 |
|
Wykres zależności logarytmu naturalnego liczby zliczeń w jednostce czasu Ii od masy absorbenta na jednostkę jego powierzchni px.
ρx[mg/cm2] |
Ii[imp/min] |
Ln Ii[1] |
0,00 |
85 |
4,44 |
62,4 |
80 |
4,38 |
133,8 |
57 |
4,04 |
178,4 |
43 |
3,76 |
249,8 |
30 |
3,40 |
303,3 |
27 |
3,29 |
365,7 |
25 |
3,22 |
Wyznaczanie równania prostej aproksymującej:

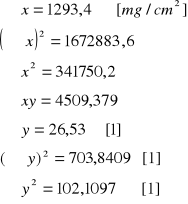
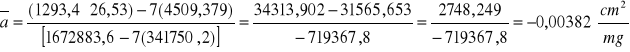

![]()
![]()

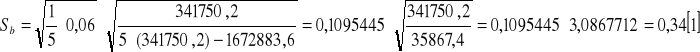

Wyznaczanie masowego współczynnika pochłaniania elektronów i wartości liniowego pochłaniania.
Porównując równanie prostej ln Ii = a ρx + b
z równaniem ln N = a ρx + b
gdzie:
a = - ![]()
/![]()
b = ln No
otrzymujemy wzór na masowy współczynnik pochłaniania
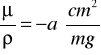
gdzie:
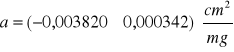
współczynnik prostej aproksymującej
zależność ln Ii = f(ρx)
masowy współczynnik pochłaniania wynosi 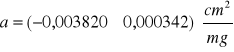
=
= (3,82±0,34)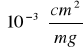
Na podstawie masowego współczynnika pochłaniania wyznaczamy liniowy współczynnik pochłaniania:
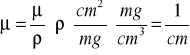
gdzie:
![]()
(3,82±0,34)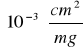
- masowy współczynnik pochłaniania
ρ= 8960![]()
gęstość miedzi
![]()
Obliczanie niepewności liniowego współczynnika pochłaniania metodą różniczki zupełnej.
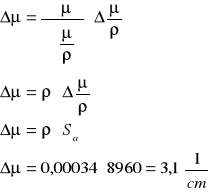
Liniowy współczynnik pochłaniania wynosi ![]()
7.Odczytanie wartości odciętej xmax.
Maksymalny zasięg xmax promieniowania w miedzi odczytujemy jako odciętą punktu przecięcia się prostej aproksymującej ln Ii = a ρx + b z prosta określającą poziom szybkości zliczeń It promieniowania tła.
ln Ii = a ρx + b
![]()
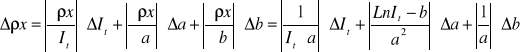
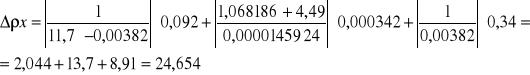
![]()
,![]()
= (332,461±24,654) ![]()
8.Wykres zależności zasięgu maksymalnego max promieniowania beta od jego energii maksymalnej Emax.
|
100 |
150 |
200 |
250 |
300 |
400 |
500 |
800 |
1000 |
|
13,5 |
26,5 |
42 |
59 |
78 |
120 |
165 |
310 |
420 |
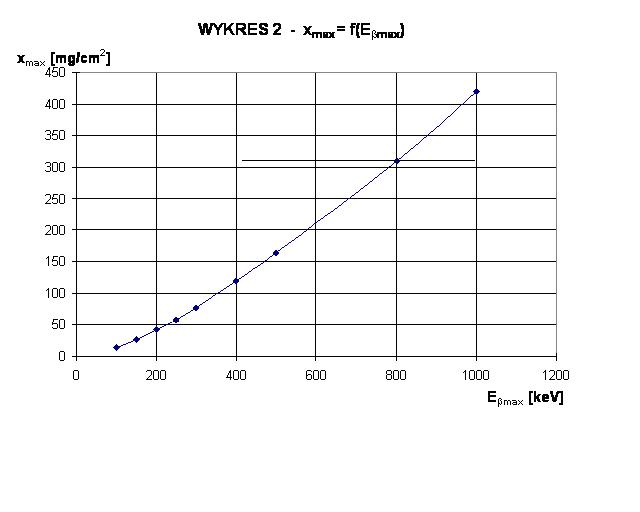
E max = 800 [keV]
Zestawienie wyników:
It=(11,700±0,092)[imp/min]
![]()
(3,82±0,34)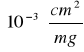
- masowy współczynnik pochłaniania
![]()
- liniowy współczynnik pochłaniania.
y=-0,004x+4,5465 - prosta aproksymująca
![]()
,![]()
= (332,461±24,654) ![]()
E max = 800 [keV]
9.Wnioski
Celem wykonanego przez nas ćwiczenia było wyznaczenie maksymalnej energii i zasięgu promieniowania beta w ciałach stałych. Grupa dziekańska przeprowadzała ćwiczenie laboratoryjne przy użyciu absorbentów miedzianych.
Dokładność wykonanych pomiarów uwarunkowana była dokładnością dysponowanego przez nas sprzętu, a także przybliżonych wartości kolejnych zliczeń licznika Geigera - Müllera.
![]()
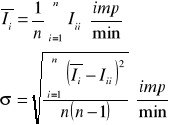
![]()
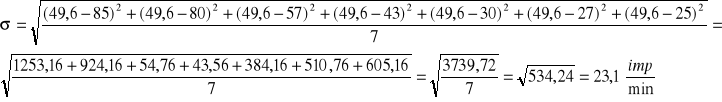
![]()

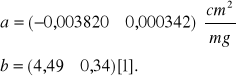
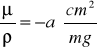
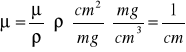
![]()
![]()
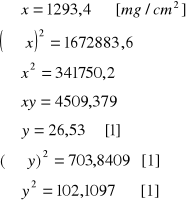
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Opracowanie wyników II bez średniej i odchylenia, Politechnika śląska katowice, Zip, Semestr III, Fi
Opracowanie wyników, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL,
Galwanometron, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Spraw
Karta pomiarowa, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fiz
betabartek, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyka l
Fiza-pojecia, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyka
krzywebartek, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyka
Monochromator, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyk
SEM-DZIDA, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Sprawka,
Fizyka wykład 220507, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL
termin 2, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyka lab
qlki, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyka lab skr
SEM-Luda, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Sprawka, s
zipprzewodnikibartekpopr, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BU
lisarzuuuuu, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizyka
elipsoidabartek, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fiz
sprawozdanie 12 got zal, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BUR
Promieniowanie Beta, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL,
Radioaktywnosc, Politechnika śląska katowice, Zip, Semestr III, Fizyka, Lab, fizyka lab BURDEL, Fizy
więcej podobnych podstron