I. Przebieg ćwiczenia.

1. Zapoznanie się z charakterystyką licznika Geigera-Mullera oraz ustalenie napięcia pracy licznika.

2. Wyznaczenie natężenia promieniowania tła poprzez pomiar liczby zliczeń licznika Geigera-Mullera bez preparatu promieniotwórczego w jego pobliżu.

3. Pomiar liczby zliczeń w obecności absorbenta dla różnych jego grubości.

4. Przerwanie pomiarów, gdy liczba zliczeń zrównała się z liczbą zliczeń odpowiadającą promieniowaniu tła.

II. Opracowanie wyników

a) Obliczenie dla promieniowania tła liczby zliczeń It licznika Geigera-Mullera w jednostce czasu.

Liczbę zliczeń I_t [imp/min] obliczamy ze wzoru:

gdzie:

N - liczba zliczeń licznika zarejestrowana w trakcie pomiaru

t - czas pomiaru

I_t=3,33 /0,1667

Wartość średnia i odchylenie standardowe:

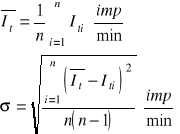
Obliczona średnia wartość liczby zliczeń tła na jednostkę czasu wynosi:

I_t = (10 ± 0,8) [imp/min].

b) Obliczenie masy absorbenta na jednostkę powierzchni.

Do obliczeń wykorzystujemy wzór:

gdzie:

ρ = 8960 [kg/m³ = mg/cm³] - gęstość miedzi

x - zmierzona grubość folii

x [mm]	ρx [mg/cm ]
0,008	72
0,016	143
0,024	215
0,032	286
0,040	358
0,048	430
0,056	502
0,064	573

c) Obliczenie liczby zliczeń Ii licznika Geigera-Mullera w jednostce czasu.

Liczbę zliczeń I_i [imp/min] obliczamy ze wzoru:

gdzie:

N - liczba zliczeń licznika zarejestrowana w trakcie pomiaru

t - czas pomiaru

liczba folii	x [mm]	Ii [imp/min]
1	0,008	144
2	0,016	140
3	0,024	112
4	0,032	72
5	0,040	60
6	0,048	32
7	0,056	28
8	0,064	16

d) Wykres zależności logarytmu naturalnego liczby zliczeń w jednostce czasu Ii od masy absorbenta na jednostkę jego powierzchni px.

x [mg/cm^2]	Ii [imp/min]	ln Ii [1]
72	144	6,01
143	140	5,80
215	112	5,46
296	72	5,35
358	60	5,32
430	32	5,23
562	28	4,97
573	16	4,79

e) Wyznaczenie równania prostej aproksymującej.

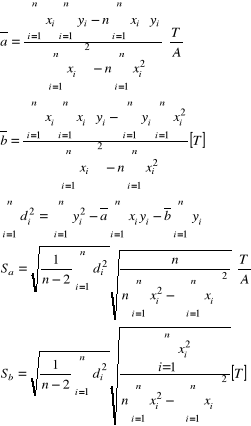
a = - (5± 0) ×10^{- 3} [cm²/mg]

b = (5545 ± 16) ×10^{- 3} [1].

f) Wyznaczenie masowego współczynnika pochłaniania elektronów i wartości liniowego współczynnika pochłaniania.

Porównując równanie prostej

ln I_i = a
x + b

z równaniem

ln N = a
x + b

gdzie:

a = -
/

b = ln N_o

otrzymujemy wzór na masowy współczynnik pochłaniania:

gdzie:

a = - (5± 0) ×10^{- 3} [cm²/mg] - współczynnik prostej aproksymującej zależność

ln I_i = f(
x).

Masowy współczynnik pochłaniania wynosi: (5± 0) ×10^{- 3} [cm²/mg].

Na podstawie masowego współczynnika pochłaniania wyznaczamy liniowy współczynnik pochłaniania:

gdzie:

(5± 0) ×10^{- 3} [cm²/mg] - masowy współczynnik pochłaniania

ρ = 8960 [kg/m³ = mg/cm³] - gęstość miedz.

 = 44,8 [1/cm].

Obliczanie niepewności liniowego współczynnika pochłaniania metodą różniczki zupełnej.

Δμ =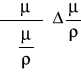

Δμ =

Δμ =

Δμ = 0 [1/cm].

Liniowy współczynnik pochłaniania wynosi:  = 44,8 ± 0 [1/cm]

g) Odczytanie wartości odciętej xmax

Maksymalny zasięg x_max promieniowania  w miedzi odczytujemy jako odciętą punktu przecięcia się prostej aproksymującej ln I_i = a ρx + b z prosta określającą poziom szybkości zliczeń I_t promieniowania tła.

Na wykresie 1 prosta aproksymująca nie przecina się z wyznaczoną linią prostą poziomu szybkości zliczeń I_t promieniowania tła, więc wartość x_max została wyliczona w następujący sposób:

ln I_i = a ρx + b

= 503,00 [mg/cm²]

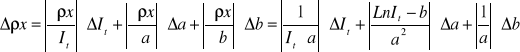
Maksymalny zasięg promieniowania  w miedzi wynosi:

x_max = (503 ± 0,8) [mg/cm²]

III. Wnioski

1. Podsumowanie:

• (50 ± 0) ×10^{- 3} [cm²/mg] - masowy współczynnik pochłaniania

•  = (141,5 ± 8,9) [1/cm] - liniowy współczynnik pochłaniania.

2. Dla liczby zliczeń licznika znacznie różniących się od liczby zliczeń promieniowania tła zależność ln I_i = f(ρx) ma charakter liniowy.
Aproksymację przeprowadziliśmy jedynie dla trzech wyników, dla których szybkość zliczeń impulsów była wyraźnie większa od szybkości I_t pochodzących od promieniowania tła.

3. Niedokładności wyników są spowodowane błędami pomiaru czasu zliczeń licznika Geigera-Mullera, oraz błędami wyznaczenia współczynników prostej aproksymującej zależność ln I_i = f(ρx).

4. Maksymalny zasięg promieniowania  w miedzi obliczony przez podstawienie do wzoru prostej aproksymującej wartości poziomu szybkości zliczeń tła wynosi

x_max = (503 ± 0,8) [mg/cm²].

Politechnika Śląska Katowice 09.03.2011

Wydział Transportu

ĆWICZENIA LABOLATORYJNE Z FIZYKI

Sprawozdanie z ćwiczenia nr 8

Temat ćwiczenia: Wyznaczanie maksymalnej energii i zasięgu promieniowania β w ciałach stałych.

Grupa T14

Sekcja nr 8

Aleksander Osmałek

Bartosz Pałka

---