Składanie drgań

Drgania równoległe

Jaki będzie wynik nałożenia się dwóch drgań harmonicznych x_a oraz x_b o kierunkach równoległych, ale różnych częstościach, amplitudach i fazach? Dla zbadania formy tego ruchu złożonego zapiszmy równania ruchu dla obu drgań składowych oraz ich sumę.

 

,

suma

(6.39)

Intuicyjnie przewidujemy, że w chwili czasu, kiedy oba wychylenia są w tym samym kierunku - otrzymamy wzmocnienie, kiedy w przeciwnym - osłabienie sumarycznego wychylenia, x.
Rozpatrzmy bliżej szczególny przypadek, kiedy obie częstości różnią się niewiele. Dla uproszczenia przyjmiemy, że amplitudy i fazy są takie same, a różnica ich częstości  jest niewielka.

 

,

(6.40)

Po dokonaniu przekształceń trygonometrycznych ich suma może być zapisana w postaci

 

.

(6.41)

(Dla uproszczenia zaniedbaliśmy  /2 w drugim czynniku jako znacznie mniejsze od  Wzór ten opisuje także ruch harmoniczny, ale z amplitudą zadaną przez bezwzględną wartość pierwszego czynnika po jego prawej stronie. Amplituda jest teraz także funkcją czasu, ale o częstości znacznie mniejszej, bowiem określonej przez połowę różnicy częstości drgań składowych. Zjawisko to nazywamy dudnieniem. 

W ogólnym przypadku, gdy częstości _a i _b różnią się dowolnie, wypadkowy ruch może nie być ruchem harmonicznym, a nawet może nie być ruchem okresowym. Ruch okresowy otrzymamy gdy częstości składowych ruchów spełniają warunek _a/ _b= n_a/n_b, gdzie n_a i n_b są liczbami całkowitymi. Oznacza to, że częstości ruchów składowych dają się przedstawić jako całkowita wielokrotność pewnej częstości podstawowej  ( _a=n_a_, _b= n_b). Jak widać z równań (39), kiedy _a=  _b, ruch wypadkowy jest ruchem harmonicznym o takiej samej częstości jak ruchy składowe oraz o amplitudzie i fazie początkowej zależnej od amplitud i faz początkowych obu drgań składowych.

Interaktywna ilustracja graficzna

Załączona interaktywna ilustracja graficzna umożliwia modyfikowanie nie tylko różnicy częstości, ale także niezależne zmiany amplitud i faz obu drgań. Sprawdź jak zmiany te wpływają na formę drgań sumarycznych.

MS-Excel	Interaktywna ilustracja graficzna	Kliknij w polu rysunku.
Rys.12.4. Położenie, prędkość i przyspieszenie w ruchu harmonicznym.

 

Drgania prostopadłe

Kiedy drgania punktu materialnego odbywają się równocześnie w dwóch prostopadłych do siebie kierunkach, np. wzdłuż osi x i y prostokątnego układu współrzędnych, to wypadkowy ruch tego punktu na płaszczyźnie można opisać z pomocą równań postaci:

(6.42)

(6.43)

 

gdzie  jest różnicą faz obu drgań składowych. Zwróćmy uwagę, że jeśli częstości drgań są jednakowe i różnica faz wynosi zero lub , to równanie toru punktu będzie odcinkiem prostej o równaniu

(6.44)

lub odpowiednio

(6.44a)

 

Kiedy zaś różnica faz =± /2 , to równanie (43) można zapisać jako

 

(6.45)

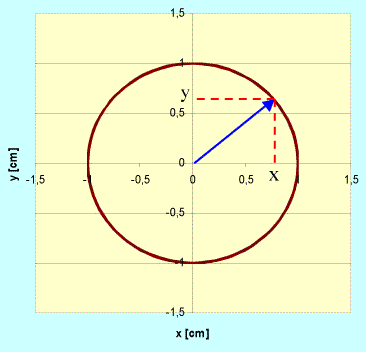
W tym przypadku, gdy _x=  _y, układ poruszać się będzie po elipsie, która przejdzie w okrąg kiedy A_x = A_y. Dochodzimy do następującego stwierdzenia.

Jeżeli punkt materialny porusza się ruchem jednostajnym po okręgu w płaszczyźnie (x, y), to ruch jego rzutu na osie układu współrzędnych jest ruchem harmonicznym.

To interesujące stwierdzenie łączy ruch harmoniczny z ruchem jednostajnym po okręgu.

Figury Lissajou

 Podana wyżej relacja pomiędzy ruchem harmonicznym i ruchem po okręgu jest jednak tylko przypadkiem szczególnym składania harmonicznych drgań prostopadłych. Kiedy częstości drgań w obu kierunkach różnią się, to punkt tworzy skomplikowane figury zwane figurami Lissajou. Figury te mieszczą się w prostokącie o wymiarach 2A_x, i 2A_y. Stosunek liczby punktów stycznych do obu boków prostokąta wyznacza stosunek częstości obu ruchów składowych _x/_y = n_x /n_y. Rysunek poniżej  pokazuje przykład takich figur. Całą ich "gamę" możesz wygenerować sam za pomocą załączonej interaktywnej ilustracji graficznej

MS-Excel	Interaktywna ilustracja graficzna	Kliknij w polu rysunku.
Rys.12.4. Przykład figury Lissajou.

---