Dominik Stawiński A-42 29.03.2006

Sprawozdanie T4

Temat: Wyznaczanie krzywej gięcia i jej zastosowanie w projektowaniu procesów

Cel:

Celem ćwiczenia jest wyznaczanie charakterystyki własności plastycznych materiału, która umożliwia obliczanie pracy odkształcenia plastycznego w procesach gięcia, oraz momentu gnącego.

Wstęp:

Plastyczne kształtowanie wyrobów giętych wymaga dokładnego wyliczenie momentu gnącego, który jednak jest uzależniony od wielu złożonych zjawisk takich jak: krzywoliniowy rozkład naprężeń w poprzecznym przekroju giętego elementu, czy też zmniejszanie się grubości elementu. Wyznaczana doświadczalnie charakterystyka własności plastycznych, przydatna tylko w procesach gięcia, pozwala wyznaczyć ten moment z dokładnością wystarczającą do zastosowań praktycznych. Charakterystyka własności plastycznych musi być niezależna od wymiarów próbki i daje się to osiągnąć dzieląc moment M przez wskaźnik wytrzymałości na zginanie poprzeczne przekroju elementu, oraz mnożąc krzywiznę 1 / ρ przez znaną grubość giętej blachy. Uzyskujemy w ten sposób zależność zastępczych naprężeń gnących б_c od względnej krzywizny g / ρ .

Przebieg ćwiczenia:

W ćwiczeniu dokonaliśmy zginania próbki na maszynie wytrzymałościowej i otrzymaliśmy wykres zależności siły P użytej do gięcia od rozsunięcia u uchwytów maszyny wytrzymałościowej. Na podstawie tego wykresu sporządzamy krzywe zależności Б_g (r_w/g) , oraz λ (r_w/g) dla badanego materiału. Wyniki obliczeń zamieszczamy w tabeli 1. .

Tabela 1.

m [mm]	11	21,5	31	41	51	60,5	71	82	91,2	101,5	112	122	132	142	155
P'[N]	596,6	631,0	658,6	675,9	689,7	710,3	720,7	734,5	744,8	758,6	772,4	780,7	786,2	796,6	792
g/ρc[1]	0,0253	0,0483	0,0713	0,0943	0,1174	0,1392	0,1634	0,1875	0,2099	0,2336	0,2577	0,2807	0,3037	0,3267	0,7133
Бg [MPa]	763,01	807,11	842,40	864,45	882,09	908,56	921,79	939,43	952,66	970,30	987,94	998,53	1005,59	1018,82	1020
rw/g [1]	39,009	20,195	13,519	10,100	8,021	6,683	5,621	4,832	4,265	3,782	3,380	3,062	2,792	2,561	0,902
λl	0,91	0,905	0,903	0,9	0,89	0,88	0,87	0,86	0,85	0,845	0,84	0,83	0,827	0,82	0,818

Parametry i współczynniki:

G₁= 0,65 kG a= 44mm R= 80,4mm k= 2

g=1,85mm l= 10mm P_max=79,2kg=792N b=55,1 mm

.

gdzie:

G₁- siła ciężkości głowicy maszyny i cięgien

a- ramię działania siły

R- ramię siły P₁

g- grubość próbki

l- długość nieobciążonej płytki

b- szerokość próbki

W wyliczaniu wartości w tabeli korzystałem ze wzorów:

P'- wartość siły działającej na materiał

g/ ρ_c- względna krzywizna

g/ ρ_c=

Б_g- zastępcze naprężenia gnące

Б_g=

r_w/g =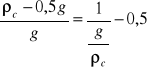

Wyznaczam kąt ugięcia:

α=
= 155 / 80,4 = 1,883 rad = 105,35^o

Wnioski:

Na podstawie otrzymanych wykresów można stwierdzić, ze naprężenia rosną najszybciej w pierwszej fazie zginania, wtedy gdy promień r_w ma małą wartość. Kiedy pokonamy odkształcenia sprężyste materiału przyrost naprężenia w funkcji promienia r_w jest już wolniejszy ( g jest wartością stałą). Odwrotną sytuację mamy w przypadku współczynnika wypełnienia wykresu λ_l .Największy jest dla małych wartości promienia. Wraz ze wzrostem promienia zaczyna spadać i również na początku ten spadek jest szybki, a gdy materiał wejdzie w stan --> napręże[Author:D] ń plastycznych λ_l maleje powoli. Wyznaczony kąt α jest praktycznie równy rzeczywistemu kątowi zagięcia α_rz = ok. 106 ^o .Różnice mogą wynikać z niedokładnych pomiarów wielkości próbki, a także z faktu, że współczynnik k jest tylko w przybliżeniu równy 2.

---