Katedra Metrologii Elektronicznej i Fotonicznej LABORATORIUM MIERNICTWA ELEKTRONICZNEGO
Temat ćwiczenia: Statystyczna analiza wyników pomiarów
Wykonał: Tomasz Muciek Termin zajęć: wtorek 15.00-17.15 Grupa: 5
Data wykonania: 4.03.2003 Data oddania: 11.03.2003
Prowadzący: Dr inż. Z. Świerczyński Ocena: |
Cel ćwiczenia:
Celem ćwiczenia jest zapoznanie się ze statystyczną analizą wyników pomiarów, sposobami znajdowania i eliminacji wyników obarczonych błędami grubymi oraz oceną składowej przypadkowej błędu, a także wskazanie na konieczność analizy warunków i wyników pomiarów pod kątem obecności składowej systematycznej błędu.
Analiza i opracowanie wyników pomiarów
Tabele wyników pomiarów dla trójkąta nr 7.
Tabela 1.1. Pomiary boków i wysokości trójkąta nr 7..
Lp. |
a [mm] |
b [mm] |
c [mm] |
ha [mm] |
hb [mm] |
hc [mm] |
1. |
93,95 |
84,55 |
75,34 |
64,6 |
71,72 |
80,48 |
2. |
93,83 |
84,54 |
75,31 |
64,62 |
71,76 |
80,55 |
3. |
93,95 |
84,56 |
75,3 |
64,62 |
71,71 |
80,46 |
4. |
95,18 |
85,47 |
75,81 |
64,96 |
72,29 |
81,55 |
5. |
93,67 |
84,48 |
75,23 |
64,51 |
71,68 |
80,44 |
6. |
93,83 |
84,48 |
75,25 |
64,49 |
71,63 |
80,42 |
7. |
93,92 |
84,56 |
75,34 |
64,6 |
71,72 |
80,47 |
8. |
93,81 |
84,55 |
75,32 |
64,6 |
71,71 |
80,45 |
9. |
93,92 |
84,54 |
75,32 |
64,61 |
71,72 |
80,46 |
10. |
93,88 |
84,54 |
75,3 |
64,52 |
71,68 |
80,43 |
11. |
93,89 |
84,5 |
75,24 |
64,59 |
71,7 |
80,46 |
12. |
93,95 |
84,57 |
75,36 |
64,61 |
71,74 |
80,48 |
m |
93,981 |
84,611 |
75,343 |
64,610 |
71,755 |
80,554 |
s |
0,3859 |
0,2720 |
0,1526 |
0,1190 |
0,1716 |
0,3153 |
Tabela 1.2. Obliczenia pól trójkąta nr 7.
Lp. |
Pa [mm2] |
Pb [mm2] |
Pc [mm2] |
Ph [mm2] |
1. |
3034,6 |
3032 |
3031,7 |
3024,1 |
2. |
3031,6 |
3033,3 |
3033,1 |
3021 |
3. |
3035,5 |
3031,9 |
3029,3 |
3023,1 |
4. |
3091,4 |
3089,3 |
3091,2 |
3082,1 |
5. |
3021,3 |
3027,8 |
3025,8 |
3014,4 |
6. |
3025,5 |
3025,7 |
3025,8 |
3017,5 |
7. |
3033,6 |
3032,5 |
3031,3 |
3023,9 |
8. |
3030,1 |
3031,5 |
3029,7 |
3021,3 |
9. |
3034,1 |
3031,6 |
3030,1 |
3022,7 |
10. |
3028,6 |
3029,9 |
3028,2 |
3021,5 |
11. |
3032,2 |
3029,3 |
3026,9 |
3018,7 |
12. |
3035,1 |
3033,5 |
3032,5 |
3025,2 |
m |
3036,1 |
3035,6 |
3034,6 |
3026,3 |
s |
17,0 |
17,0 |
18,0 |
17,8 |
Sprawdzanie, czy pomiary były obciążone błędami grubymi i ewentualne
przeprowadzenie eliminacji lub korekty tych błędów.
Po przeanalizowaniu wyników pomiarów można stwierdzić, że student 4 podczas pomiaru boków a, b, c, oraz wysokości hb, hc, popełnił błędy grube. Wynik tych pomiarów (zaznaczone na czerwono) wykraczają poza przedział, w którym (zgodnie z funkcją Gaussa rozkładu gęstości prawdopodobieństwa) powinno znajdować się 99,7% wyników. Mogło to być spowodowane błędnym odczytem z suwmiarki lub pomyłką przy wprowadzaniu danych do pamięci komputera. Wyniki tych pomiarów oraz pola trójkątów policzone na podstawie tych wyników powinny zostać odrzucone.
Wyniki obliczeń wartości średniej oraz odchylenia standardowego, po odrzuceniu pomiarów zawierających błędy grube przedstawia tabela 1.3 oraz 1.4
Tabela 1.3
Lp. |
a [mm] |
b [mm] |
c [mm] |
ha [mm] |
hb [mm] |
hc [mm] |
m |
93,872 |
84,533 |
75,301 |
64,611 |
71,706 |
80,464 |
s |
0,0845 |
0,0320 |
0,0432 |
0,1190 |
0,0344 |
0,0344 |
Tabela 1.4
Lp. |
Pa [mm2] |
Pb [mm2] |
Pc [mm2] |
Ph [mm2] |
m |
3031,1 |
3030,8 |
3029,4 |
3021,2 |
s |
4,46 |
2,41 |
2,57 |
3,22 |
Analiza miar błędów przypadkowych.
Z przeprowadzonych pomiarów wynika, że:
największe odchylenia standardowe w grupie pomiarów boków występują przy pomiarze długości boku a,
największe odchylenia standardowe w grupie pomiarów wysokości występują przy pomiarze wysokości poprowadzonej na bok a,
wartości odchyleń standardowych pomiarów boków są porównywalne z wartościami odchyleń standardowych wysokości, nie można jednoznacznie stwierdzić, że w którejś z grup pomiarów błąd przypadkowy jest większy.
Odchylenia, które wystąpiły mogły być spowodowane wieloma przyczynami np.
- stosunkowo trudnym ustawieniem mierzonej wysokości trójkąta prostopadle do szczęk suwmiarki,
- zaokrąglenia wierzchołków trójkąta ,
- różnego ścisku suwmiarki stosowanego przez mierzących,
Analiza błędów systematycznych wyznaczenia powierzchni trójkąta.
Rozmiary obliczonych pól zarówno ze wzoru standardowego jak i wzoru Herona są bardzo do siebie zbliżone. Niemniej jednak pola wyliczona ze wzoru Herona, są mniejsze co do wartości od pól liczonych ze wzoru tradycyjnego. Spowodowane to jest tym że we wzorze Herona wykorzystywane są długości wszystkich trzech boków trójkąta. Pomiary boków ze względu na trudności zmierzenia boku miały tendencję do zaniżania swej wartości. We wzorze tradycyjnym wykorzystuje się tylko jeden bok i opadająca na niego wysokość. Pomiary wysokości z kolei miały skłonność do zawyżania swej wartości.
Najmniejszy błąd przypadkowy zawierały pola liczone z wykorzystaniem boku b i wysokości hb, oraz boku c i wysokości hc.
Zestawienie wyników pomiarów przedstawiają tabele 1.5, 1.6.
Tabela 1.5
|
m |
n |
s |
sx= |
Δp=3sx
|
Δn |
δp= |
δn= |
Ostateczny wynik pomiaru m±(Δp+Δn) |
|
mm |
- |
mm |
mm |
mm |
mm |
% |
% |
mm |
a |
93,872 |
11 |
0,0845 |
0,0255 |
0,0765 |
0,03 |
0,0815 |
0,0319 |
93,87± 0,11 |
b |
84,533 |
11 |
0,0320 |
0,0096 |
0,0288 |
0,03 |
0,0340 |
0,0354 |
84,53± 0,06 |
c |
75,301 |
11 |
0,0432 |
0,0130 |
0,0390 |
0,03 |
0,0518 |
0,0398 |
75,30±0,07 |
ha |
64,611 |
12 |
0,1190 |
0,0412 |
0,1236 |
0,03 |
0,1913 |
0,0464 |
64,61± 0,15 |
hb |
71,706 |
11 |
0,0344 |
0,0103 |
0,0309 |
0,03 |
0,0431 |
0,0418 |
71,71±0,06 |
hc |
80,464 |
11 |
0,0344 |
0,0103 |
0,0309 |
0,03 |
0,0384 |
0,0372 |
80,46± 0,06 |
Tabela 1.6
|
m |
N |
s |
sx= |
Δp=3sx
|
Δn=Δn*a + Δn*h
|
δp= |
δn=δna+δnh
|
Ostateczny wynik pomiaru m±(Δp+Δn) |
|
mm2 |
- |
mm2 |
mm2 |
mm2 |
mm2 |
% |
% |
mm2 |
Pa |
3031,1 |
11 |
4,46 |
1,345 |
4,035 |
4,754 |
0,1331 |
0,0783 |
3031,1± 8,79 |
Pb |
3030,8 |
11 |
2,41 |
0,727 |
2,181 |
4,687 |
0,0720 |
0,0772 |
3030,8±6,87 |
Pc |
3029,4 |
11 |
2,57 |
0,775 |
2,325 |
4,673 |
0,0767 |
0,0760 |
3029,4±7,00 |
Ph |
3021,2 |
11 |
3,22 |
0,971 |
2,913 |
-------- |
---------- |
---------- |
--------------- |
a, b, c - boki trójkąta;
ha, hb, hc - wysokości trójkąta;
m - średnia arytmetyczna n pomiarów;
![]()
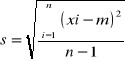
s - odchylenie średnie kwadratowe;
sx - odchylenie średniej arytmetycznej;
Δp - błąd przypadkowy graniczny pomiaru ;
Δn - błąd graniczny suwmiarki;
δp - błąd względny przypadkowy;
δn - błąd względny suwmiarki;
δna - błąd względny pomiaru boku
δnh - błąd względny pomiaru wysokości
Wyznaczenie minimalnej liczby pomiarów boków i wysokości, tak aby błąd przypadkowy był pomijalnie mały.
![]()
10Δp < Δn ⇒ 10∗3sx<Δn ⇒ 10∗3![]()
<Δn ⇒ n>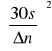
![]()
⇒ n>(1000s)2
Δn=0.03mm
Tabela 1.7
|
a |
b |
c |
ha |
hb |
hc |
s[mm] |
0,0845 |
0,0320 |
0,0432 |
0,1190 |
0,0344 |
0,0344 |
n |
7056 |
1024 |
1849 |
14161 |
1156 |
1156 |
s - odchylenie średnie kwadratowe;
n- ilość pomiarów, którą należy wykonać by błąd przypadkowy średniej arytmetycznej był pomijalnie mały
Wnioski:
Podczas wykonywania pomiarów student na stanowisku nr 4 popełnił błędy grube. Błędy te zostały skorygowane podczas opracowywania wyników pomiarów. Mogły one nastąpić w wyniku nieprawidłowego wpisu do komputera lub pomyłki przy odczycie wartości.
Największe odchylenia standardowe wystąpiły przy pomiarze długości boku a i wysokości poprowadzonej na ten bok. Trudno powiedzieć jaka jest tego przyczyna. Teoretycznie odchylenie standardowe w grupie pomiarów wysokości powinno być większe niż w grupie pomiarów boków.
Rozmiary obliczonych pól zarówno ze wzoru standardowego jak i wzoru Herona są bardzo do siebie zbliżone. Niemniej jednak pola wyliczona ze wzoru Herona, są mniejsze co do wartości od pól liczonych ze wzoru tradycyjnego.
Najmniejszy błąd przypadkowy zawierały pola liczone z wykorzystaniem boku b i wysokości hb, oraz boku c i wysokości hc.
Aby błąd przypadkowy średniej arytmetycznej był pomijalnie mały należy wykonać bardzo dużo pomiarów (Tabela 1,7). Najwięcej dla boku a oraz wysokości poprowadzonej na ten bok.
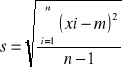
Wyszukiwarka
Podobne podstrony:
Formatki protokołów z ćwiczeń laboratoryjnych, Protokoły4dm2, Analiza błędów pomiaru posredniego
Cw 1 protokół pomiarów i obliczeń
Protokoły, Ćwiczenie 11 - Pomiar kół zębatych, AKADEMIA TECHNICZNO-ROLNICZA W BYDGOSZCZY
Protokoły, Ćwiczenie 6 - Pomiar krzywek wałka rozrządu, AKADEMIA TECHNICZNO-ROLNICZA W BYDGOSZCZY
PROTOKÓŁ POMIAROWY ćw C, Studia, ZiIP, SEMESTR II, Mechanika
Cw 3 protokół pomiarów i obliczeń
ćw 24 ćwiczenie$
metrologia cw 4 protokol
mikrobiologia ćw 3, Dokończenie ćwiczenia 2
Ćw nr 9, ćwiczenie 9, Paweł karaś
ćwiczenia, Praca domowa ćw 2, Chemia ćwiczenia, I rok IŚ, studia stacjonarne 2009/2010
CW NR2b, ĆWICZENIE Nr 2
pomiary cw 4f
cw 2 Opis ćwiczenia
Badanie dokładności przyrządu pomiarowego Cw 4
METROLOGIA, METROLOGIA - 11 - Pomiary gwintów metrycznych, Ćwiczenie Nr 2 - Pomiar średnicy otworów
CW NR1b, ĆWICZENIE Nr 1
Traumatologia, traumatologia cw I-sciagi[1], Ćwiczenia I
więcej podobnych podstron