Nr. ćw. 102 |
Data 28.03.01 |
Jakacki Zbigniew |
Wydział Elektryczny |
Semestr II |
Grupa E-3 |
Prowadzący: mgr B. Jazurek |
Przygotowanie |
Wykonanie |
Ocena
|
||
Temat: Wyznaczanie modułu sztywności metodą dynamiczną
Wyznaczenie moduł sztywności można dokonać stosując metodę statyczną lub dynamiczną. Metoda statyczna przeznaczona jest dla cienkich prętów i drutów a dynamiczna dla znacznych przekrojów.
W ćwiczeniu wykorzystamy metodę dynamiczną gdyż badany drut ma niewielki przekrój. Jest on swym górnym końcem przymocowany do nieruchomego uchwytu, zaś na dolnym przymocowany jest wibrator. Wibrator składa się z dwóch skrzyżowanych płaskowników na których są przymocowane kołki umożliwiające nakładania obciążeń.
![]()
Skręcając wibrator o pewien kąt powodujemy wystąpienie w drucie momentu sił sprężystości. Działający moment stara się przywrócić stan równowagi. Zwolniony wibrator zacznie wykonywać ruch drgający czyli harmoniczny o okresie
gdzie: I- moment bezwładności, D - moment kierujący.
![]()
Moment kierujący wyznaczamy z zależności
![]()
Wyznaczenie momentu bezwładności nieobciążonego wibratora jest trudne, dlatego staramy się weliminować tę wielkość poprzez umieszczenie tzw. obciążenia wstępnego. Wówczas moment bezwładności zwiększy się o I1, a wzór przyjmie postać
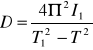
Przekształcając powyższe zależności można się pozbyć I a tym samym wyznaczyć moment kierujący który przedstawia poniższy wzór
![]()
Ostateczne równanie modułu skręcenia przyjmuje postać
gdzie: l - długość drutu, r - promień drutu, T - okres drgań wibratora nieobciążonego lub obciążonego wstępnie, T1 - okres drgań wibratora obciążonego znanymi masami.
Dodatkowy moment bezwładności można uzyskać poprzez nakładanie walców (obciążeń) o znanych masach na odpowiednie kołki. Znając odległości walców od osi wibratora d oraz ilość walców N, a także ich masę zgodnie z twierdzeniem o osiach równoległych Steinera można wyznaczyć moment bezwładności układu zgodnie z zależnością:
I1=NI0+Nmd2
gdzie: I0 - moment bezwładności pojedynczego walca względem jego osi symetrii.
1. Długość badanego drutu
l = 165 ± 1 [mm]
2. Średnica drutu 2r (10 pomiarów)
Pomiar |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Średnica drutu [mm] |
1,00 |
1,01 |
1,01 |
1,01 |
1,00 |
1,01 |
1,00 |
1,01 |
1,01 |
1,00 |
Uśredniając powyższe pomiary otrzymałem
φ= 1,006±0,01 [mm]
3. Okresy drgań wibratora obciążonego wstępnie dla mas w odległości d3
Pomiar |
1 |
2 |
3 |
|||
N |
10 |
20 |
10 |
20 |
10 |
20 |
t [s] |
90,5 |
180,2 |
93,0 |
185,0 |
92,0 |
179,0 |
Po uśrednieniu pomiarów czasów oraz liczby drgań otrzymałem
N = 10 t=91,8±2,5 [s]
N = 20 t=181,4±6 [s]
T = 9,12667
δT = 0,143261
4-5. Średnica użytych walców oraz poszczególne ich masy
Walec |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Średnica 2R [mm] |
31,9 |
31,7 |
32,0 |
31,8 |
32,0 |
31,7 |
31,8 |
31,8 |
31,7 |
31,8 |
31,6 |
31,5 |
Masa [g] |
95,6 |
94,5 |
95,4 |
94,3 |
94,6 |
93,6 |
94,4 |
95,6 |
93,1 |
93,8 |
91,3 |
92,0 |
Po uśrednieniu powyższych pomiarów średnic i mas walców otrzymałem
Średnica 2R=31,8±0,5 [mm] = 0,0318 [m]
Masa m=98,01±2,5 [0,09801] = 0,09801 [kg]
6. Odległości kołków d1 d2 d3 wibratora od jego środka
Kołek |
d1 |
d2 |
d3 |
Odległość od środka wibratora [mm] |
50 |
100 |
150 |
7. Okresy drgań wibratora obciążonego dla kilku rozkładów mas
Pomiar |
1 |
2 |
||
N |
10 |
20 |
10 |
20 |
t dla mas d2 d3 [s] |
105,0 |
211,0 |
100,0 |
207,0 |
t dla mas d1 d2 d3 [s] |
110,0 |
219,0 |
114,0 |
220,0 |
Po uśrednieniu powyższych pomiarów średnic i mas walców otrzymałem
N=10 dla mas d1 d2 t=102,5±5 [s]
N=20 dla mas d1 d2 t=209,0±4 [s]
N=10 dla mas d1 d2 d3 t=112,0±4 [s]
N=20 dla mas d1 d2 d3 t=219,5± 1 [s]
8. Obliczenia
![]()
Moment bezwładności dla pojedynczego walca wynosi
I0=5⋅10-5 [m2/kg]
![]()
Moment bezwładności dla układów walców znajdujących się w różnych odległościach od osi obrotu obliczamy ze wzoru ogólnego
dla N walców umieszczonych w odległościach d1 d2 d3 otrzymujemy
![]()
zatem:
I=0,00691 [m2/kg]
![]()
Moduł skręcenia obliczamy ze wzoru
Tśr = 9,1267 - dla obciążenia wstępnego
ΔT =0,1425
l = 1,655±0,001 [m] - długość drutu
T1 = 10,35 - dla dodatkowych obciążeń w d2 d3
ΔT1 = 0,0248
T1 = 11,087 - dla dodatkowych obciążeń d1 d2 d3
ΔT1 = 0,209
rśr = 0,503 [mm] - promień drutu
δr =0,002582 - odchylenie standardowe
mśr=0,0948 [kg] - masa walca
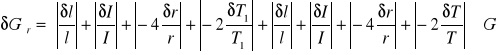
Rśr=0,0159 [m] - promień walca
![]()
Wyznaczony przez zemnie moduł sztywności przyjmuje ostateczną postać
G= 503,749±122,29 dla mas d2 d3
G=438,9635±122,32 dla mas d1 d2 d3
Otrzymany wynik nie jest zgodny z danymi tablicowymi, co mogło być spowodowane nie dokładnością pomiaru lub złą metoda obliczeń.
![]()
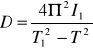
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
PAT DS 350 Graphic Modular GM Service Data
Biblia NLP Wydanie rozszerzone ponad 350 wzorcow metod i strategii programowania neurolingwistyczneg
Kolonialna ekspansja europejska, H I S T O R I A-OK. 350 ciekawych plików z przeszłości !!!
Zachodni sąsiedzi polski, H I S T O R I A-OK. 350 ciekawych plików z przeszłości !!!
Przychody państwa, H I S T O R I A-OK. 350 ciekawych plików z przeszłości !!!
MAN Ogrzewanie Webasto Thermo 230,300,350 obsługa i montaż(1)
PAT DS 350 G & GW Service Data
Ratunek po nieudanym flashu, Mio P-350, Reanimacja Mio
Orkan 350 SL
KED 350 wer z 10 2006
więcej podobnych podstron