RÓWNOWAGI FAZOWE W UKŁADACH TRÓJSKŁADNIKOWYCH

Zastosujmy regułę faz Gibbsa do układu trójskładnikowego.

Wobec tego, jeśli w układzie jest jedna faza, to :

co oznacza, że można zmieniać niezależnie od siebie cztery parametry. Nie ma żadnej możliwości przedstawienia zależności pomiędzy czterema zmiennymi nawet na wykresie przestrzennym. Wobec tego przy opisie układów trójskładnikowych dyskutuje się równowagi przy ustalonych dwu parametrach; zwykle są to temperatura i ciśnienie. Jako zmienne pozostają ułamki molowe dwu składników, gdyż ułamek molowy trzeciego jest z nimi powiązany.

W związku z tym do prezentacji równowag w układach trójskładnikowych wymyślono specjalny układ współrzędnych zwany trójkątem Gibbsa. Przedstawiony on jest na rysunku 1.

Rysunek 1. Trójkąt stężeń Gibbsa

Trójkąt Gibbsa jest to trójkąt równoboczny i w wyznaczaniu punktu odpowiadającego danemu składowi korzystamy z własności geometrycznych takiego trójkąta. Wierzchołki A, B i C odpowiadają czystym składnikom, odpowiednio A, B i C. Boki odpowiadają układom dwuskładnikowym - np. bok AB to składy mieszanin składników A i B. Na rysunku pokazano jak zmienia się ich skład wzdłuż boku. Punkty wewnątrz trójkąta odpowiadają składom mieszanin trójskładnikowych. Na odcinku RP leżą wszystkie punkty o takim samym ułamku molowym składnika C. Na odcinku LM leżą wszystkie punkty o takim samym ułamku molowym składnika B. Ich punkt przecięcia odpowiada danemu składowi mieszaniny trójskładnikowej. Ułamek molowy składnika A można znaleźć kreśląc równoległą do boku CB leżącego na przeciwko wierzchołka A. Sieczna CD to zbór punktów, dla których stosunek ułamków molowych składników A i B jest stały.

Istnieje wiele rozmaitych typów równowag w układach trójskładnikowych, zarówno pomiędzy cieczą a parą, pomiędzy rozmaitymi cieczami, cieczą i ciałem stałym, ale będziemy dyskutować tylko dwa przypadki.

Rozpuszczalność wzajemna trzech cieczy - układ dwu cieczy o ograniczonej mieszalności i trzeciej mieszającej się w sposób nieograniczony z nimi

Mówimy, że trzy ciecze wykazują całkowitą rozpuszczalność, gdy mieszają się ze sobą w każdym dowolnym stosunku. Powstaje wtedy jedna faza ciekła. Wówczas dowolny punkt w trójkącie Gibbsa przedstawia układ jednofazowy. Przykładem może być mieszanina wody, etanolu i metanolu.

Bardzo często mamy do czynienia z układami, w których dwie ciecze wykazują ograniczoną mieszalność lub wręcz są praktycznie niemieszalne. Zwykle jest to woda i jakaś niepolarna lub słabo polarna ciecz organiczna np. toluen lub chloroform. Do układu tego wprowadzamy trzecią ciecz, która miesza się w sposób nieograniczony z każdą z poprzednich. Zwykle jest to polarna ciecz organiczna np. aceton lub etanol. Początkowo w miarę dodawania jej układ jest dwufazowy. Każda z faz to trójskładnikowy roztwór, ale o innym składzie.

Rysunek 2. Wykres fazowy dla układu trzech cieczy, z których dwie (A i B) wykazują ograniczoną mieszalność, a trzecia C miesza się z nimi w sposób nieograniczony.

Na rysunku 2 pokazano sposób wyznaczania izotermy mieszalności w takim układzie. Sporządzamy mieszaninę dwu składników A i B o określonym składzie. W trójkącie Gibbsa odpowiada jej punkt D na boku AB. Punkty D' i D'' odpowiadają składom faz pozostających w równowadze w układzie dwuskładnikowym. Gdyby obie ciecze były całkowicie niemieszalne, to składom faz odpowiadałyby wierzchołki trójkąta A i B. Zaczynamy dodawać składnik C. Stosunek ułamków molowych x_A:x_B pozostaje niezmieniony czyli skład układu przesuwa się po siecznej DC. W punkcie oznaczonym M mamy układ dwufazowy. Każda z faz to roztwór nasycony o składach odpowiadających położeniom punktów M' i M'' w trójkącie Gibbsa. Linię łączącą składy obu faz nazywamy konodą. Aby ją wyznaczyć, należałoby zanalizować składy obu faz pozostających w równowadze. W miarę dodawania dalszych ilości składnika C rośnie wzajemna rozpuszczalność obu cieczy, składy obu faz stają się coraz bardziej zbliżone do siebie, aż w pewnym momencie zniknie jedna z faz i układ stanie się jednofazowy, co łatwo zaobserwować gołym okiem. Dochodzimy do punku H zwanego punktem homogenizacji. Wyznaczając punkty homogenizacji dla różnych wyjściowych składów cieczy A i B i łącząc je następnie na wykresie w trójkącie Gibbsa, otrzymujemy izotermę mieszalności zwaną binodą. Binoda dzieli pole trójkąta Gibbsa na dwa obszary. Poniżej jej mamy punkty odpowiadające układom dwufazowym, powyżej układom jednoskładnikowym.

Prawo podziału Nernsta

Rozpatrujemy układ dwu cieczy praktycznie niemieszających się z sobą. Do układu takiego dodajemy trzeci składnik (nie jest istotne czy jest on stały czy ciekły), który rozpuszcza się w obu cieczach. Gdy w układzie tym ustali się stan równowagi, potencjał chemiczny trzeciego składnika w obu cieczach jest jednakowy.

Jeśli potencjał chemiczny wyrazimy przez stężenie molowe składnika

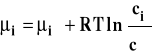
to :

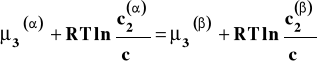
Przekształćmy to równanie tak, aby wyrazy ze stężeniem były po lewej stronie :

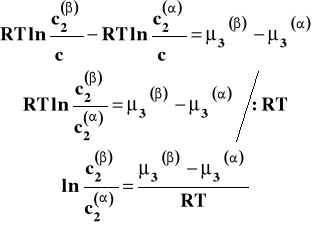
Po opuszczeniu logarytmów otrzymujemy :

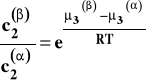
Ponieważ w danej, stałej temperaturze wartości standardowych potencjałów chemicznych są stałe, to wielkość po prawej stronie jest stała i zależy tylko od temperatury. Otrzymujemy w ten sposób prawo podziału Nernsta.

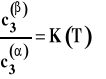
Stałą K występującą w tym wzorze nazywamy stałą (współczynnikiem) podziału Nernsta. Jej wartość zależy od temperatury. Prawo podziału Nernsta jest podstawą techniki wydzielania substancji z roztworu przez przeniesienie do innego rozpuszczalnika (ważne, aby stała K była możliwie duża) zwanej ekstrakcją oraz rozmaitych technik chromatografii podziałowej (w szczególności chromatografii cieczowej i gazowej).

R

P

M

L

D

0 x_B → 1

1 ← x_A 0

C

B

A

konoda

M''

M

M'

binoda

H

D (x_A,x_B)

C

B

A

jedna faza ciekła

dwie fazy ciekłe

D'

D''

W stałej temperaturze i pod stałym ciśnieniem w układzie dwu niemieszających się cieczy, do których dodano składnik rozpuszczalny w każdej z nich, ustala się stan równowagi, w którym stosunek stężeń tego trzeciego składnika w obu cieczach jest stały w danej temperaturze.

---