Nr ćwiczenia 14	Temat: Wyznaczanie grubości płytki kwarcowej i pomiar stężenia roztworu cukru przez pomiar kąta skręcenia płaszczyzny polaryzacji (polarymetr Laurenta)	Ocena z teorii
Nr zespołu 5	Imię i nazwisko Paweł Furman	Ocena za sprawozda.
Data 24.03.1999 r	Wydział, rok, grupa EAiE, AiR, 2	Uwagi

Światło rozchodzące się od Słońca lub innego źródła światła jest niespolaryzowane, tzn. drgania wektora świetlnego nie odbywają się prostopadle do kierunku rozchodzenia się promieni, lecz we wszystkich możliwych płaszczyznach, w których ten kierunek leży. Zazwyczaj światło jest falą bardzo złożoną, ponieważ występują równocześnie fale o różnych długościach. Celem uproszczenia sytuacji w wielu doświadczeniach stosuje się światło o długościach zawartych w bardzo małym przedziale. Zakładamy wtedy, że jest to światło monochromatyczne. Światło jest poprzeczną falą elektromagnetyczną, w której mamy do czynienia z rozchodzeniem się zmiennych pól : elektrycznego i magnetycznego. Przyjęto określać drgania świetlne tylko natężeniem pola elektrycznego E i nazwano go wektorem świetlnym. Każde źródło składa się z olbrzymiej liczby promieniujących atomów, z których każdy wysyła ciągi fal liniowo spolaryzowanych, tj. drgających w jednej płaszczyźnie. Ponieważ kierunki drgań tych źródeł są chaotyczne, nie ma więc żadnej wyróżnionej płaszczyzny, w której drgania fal byłyby intensywniejsze. Aby te chaotyczne drgania odbywały się w jednej płaszczyźnie lub według jakiegoś innego obranego porządku, to mówimy o polaryzacji światła.

W niektórych doświadczeniach ograniczamy drgania fali świetlnej tylko do jednej płaszczyzny. Mówimy wtedy, że światło jest liniowo spolaryzowane. Równanie fali światła monochromatycznego długości fali λ, spolaryzowanego liniowo w płaszczyźnie wyznaczonej kierunkami z,y przyjmuje szczególnie prostą postać

Istnieje kilka metod polaryzowania światła:

1. Przez odbicie od powierzchni dielektryka

2. Załamanie w pewnych substancjach o budowie krystalicznej

Jeśli rzucamy wiązkę promieni równoległych, pochodzących ze źródła światła naturalnego na płytkę szklaną pod dowolnym kątem α, to możemy stwierdzić za pomocą analizatora (np. pryzmat Nicola), że promień odbity jest częściowo spolaryzowany. Przy obrocie analizatora stwierdzamy zmiany natężenia wiązki przechodzącej, to znaczy że w promieniu odbitym nastąpiło pewne uporządkowanie drgań. Największe natężenie obserwujemy, gdy płaszczyzna polaryzacji analizatora jest równoległa do płaszczyzny padania wiązki na płytkę. Płaszczyznę prostopadłą do kierunku drgań wektora świetlnego nazywamy płaszczyzną polaryzacji. Powierzchnia płytki szklanej jest polaryzatorem; narzuca wektorowi świetlnemu promienia odbitego kierunek drgań prostopadły do płaszczyzny padania. Uporządkowanie drgań w promieniu odbitym nie jest całkowite i określa je tzw. stopień polaryzacji. Częściową polaryzację można wytłumaczyć tym, że amplitudy drgań wektora E w promieniu odbitym są rożne dla różnych kierunków drgań - największe w kierunku prostopadłym do płaszczyzny padania wiązki światła na płytkę, najmniejsze - w kierunku równoległym do tej płaszczyzny. Gdy zmienimy kąt padania stopień polaryzacji też ulegnie zmianie. Istnieje taki kąt, dla którego polaryzacja jest stuprocentowa - jest to kąt całkowitej polaryzacji zwany kątem Brewstera. Promień odbity zawiera wówczas tylko fale, których wektor elektryczny drga w kierunku prostopadłym. Istnieje zależność między kątem całkowitej polaryzacji, a współczynnikiem załamania ośrodka odbijającego. Całkowita polaryzacja ma miejsce, gdy promień odbity jest prostopadły do promienia załamanego.

Z definicji współczynnika załamania mamy

gdzie α - kąt padania, a w tym przypadku kąt całkowitej polaryzacji

stąd

czyli

Współczynnik n zależy od długości fali i w związku z tym kąt całkowitej polaryzacji jest różny dla różnych barw światła. Jednak różnice, z jakimi mamy do czynienia, są niewielkie. W związku z tym kąt całkowitej polaryzacji znaleziony dla pewnej średniej długości fali jest w przybliżeniu określony dla dość szerokiego zakresu widmowego. Warto zaznaczyć, że dla kąta padania α=0 (wiązka pada prostopadle na płytkę), to zarówno wiązka odbita, jak i załamana nie są spolaryzowane

Substancje krystaliczne, dzięki prawidłowemu przestrzennemu rozmieszczeniu atomów, przejawiają swoiste własności optyczne. Na ogół wektor świetlny E nie ma całkowitej swobody wykonywania drgań wewnątrz kryształu, lecz są mu narzucone tylko dwa prostopadłe do siebie kierunki drgań. Istnieje jednak jeden kierunek, który nie podlega temu warunkowi i promień biegnący wzdłuż niego ma całkowitą swobodę wykonywania drgań; jest to kierunek tak zwanej osi optycznej. Kryształy takie nazywamy jednoosiowymi, istnieją również kryształy, w których wyróżnione są dwa takie kierunki - kryształy dwuosiowe. Promień padający i kierunek osi optycznej wyznaczają płaszczyznę przecięcia głównego. Narzucone przez kryształ kierunki drgań są związane z orientacją tej płaszczyzny; jeden leży w płaszczyźnie przecięcia głównego, drugi jest do tej płaszczyzny prostopadły.

Gdy na płytkę kryształu pada prostopadła spolaryzowana wiązka promieni tak że jej kierunek nie pokrywa się z osią optyczną kryształu, wówczas wektor E rozkłada się na dwie składowe: E_n - równoległy do przecięcia głównego oraz E_z - prostopadły do E_n o następujących amplitudach

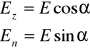
gdzie α - kąt zawarty między kierunkami lub płaszczyznami drgań w promieniu padającym i promieniu załamanym zwyczajnym. Oba drgania składowe są spolaryzowane liniowo i odpowiadają promieniowi zwyczajnemu o wektorze świetlnym E_z prostopadłym do płaszczyzny przecięcia głównego i promieniowi nadzwyczajnemu o wektorze E_n. Ponieważ strumień świetlny φ jest proporcjonalny do kwadratu amplitudy drgań wektora świetlnego E, więc dla strumieni świetlnych: zwyczajnego φ_z i nadzwyczajnego φ_n otrzymujemy:

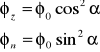
gdzie
- strumień światła padającego na płytkę

Równania te noszą nazwę praw Malusa. Jeśli płytka będzie przepuszczała tylko jeden kierunek drgań dozwolonych (np. nikol), to stosuje się tylko jedno z równań. Płytka będzie przepuszczać tylko jedno drganie składowe, drugie zostanie całkowicie wygaszone.

Światło padając na kryształ w kierunku niezgodnym do osi optycznej rozkłada się na dwa promienie spolaryzowane liniowo; promień zwyczajny i promień nadzwyczajny, drgające w płaszczyznach nawzajem prostopadłych. Oba rozchodzą się z różnymi prędkościami, mają więc różne współczynniki załamania. Uzyskanie światła spolaryzowanego wymaga więc na wyeliminowaniu jednego z promieni. Można to zrobić za pomocą pryzmatu Nicola.

Pryzmat Nicola (nikol)

Jest to pryzmat z kalcytu, czyli szpatu islandzkiego (CaCO₃) składającym się z dwóch części. Powierzchnie przecięcia sklejone są balsamem kanadyjskim o współczynniku załamania n=1,55. Tymczasem współczynniki załamania szpatu dla promienia zwyczajnego =1,66 a dla nadzwyczajnego =1,49. Kąty w pryzmacie są tak dobrane, że promień zwyczajny padając na warstwę balsamu kanadyjskiego pod kątem większym od granicznego i ulega całkowitemu wewnętrznemu odbiciu. Wychodzi przez boczne ścianki pryzmatu i zostaje pochłonięty przez czarną powierzchnię obudowy. Promień nadzwyczajny przechodzi doznając tylko niewielkiego przesunięcia równoległego.

Przepuszczając światło spolaryzowane liniowo przez płytkę z kryształu optycznie czynnego uzyskamy polaryzację kołową lub eliptyczną. Koniec wektora natężenia pola elektrycznego będzie zakreślał linię śrubową wokół kierunku rozchodzenia się fali. Światło w płytce rozpada się na wiązkę zwyczajną i nadzwyczajną. Drgania obu wiązek zachodzą w wzajemnie prostopadłych płaszczyznach. Jeżeli obydwa promienie rozchodzą się z tą samą prędkością, to po wyjściu z płytki pozostają nadal spójne, nakładają się dając taki sam wynik jak przed wejściem do płytki drgania spolaryzowane w tej samej płaszczyźnie polaryzacji. Gdy prędkości rozchodzenia są rożne dla obu wiązek, to wypadkowe drganie będzie drganiem eliptycznym, a ze względu na równoczesny ruch fali świetlnej falą spolaryzowaną kołowo lub eliptycznie. Do wytwarzania światła spolaryzowanego eliptycznie służy ćwierćfalówka.

Ćwierćfalówka

Jest to płytka krystaliczna (najczęściej mika) o grubości tak dobranej, że pomiędzy promieniem zwyczajnym i nadzwyczajnym światła przechodzącego wytwarza się różnica faz równa π/4 lub 3π/4, co odpowiada różnicy dróg optycznych λ/4 lub 3λ/4. Kierunki promienia zwyczajnego i nadzwyczajnego nazywają się azymutami. Jeżeli płaszczyzna polaryzacji światła padającego na ćwierćfalówkę jest równoległa do jednego z azymutów, wtedy światło przechodzące jest nadal spolaryzowane liniowo. W przypadku, gdy płaszczyzna polaryzacji światła padającego tworzy pewien kąt (≠0) z azymutami, wtedy drganie światła rozkłada się na promień zwyczajny i nadzwyczajny. Każdy z nich rozchodzi się z inną prędkością i po przejściu przez płytkę powstaje różnica faz λ/4 lub 3λ/4. Stąd też obydwie fale nakładając się dają w wyniku światło spolaryzowane eliptycznie. W szczególnym przypadku, gdy płaszczyzna polaryzacji światła padającego tworzy z azymutami kąt =45° otrzymujemy światło spolaryzowane kołowo.

Światło spolaryzowane liniowo przechodzące przez kryształy optycznie czynnymi doznaje skręcenia płaszczyzny polaryzacji. Dzieje się to w kryształach jednoosiowych w przypadku, gdy światło biegnie równolegle do osi optycznej. Kierunek skręcania płaszczyzny polaryzacji jest różny dla różnych kryształów, a w przypadku kwarcu znamy dwa rodzaje kryształów, z których jedne skręcają płaszczyznę polaryzacji w prawo, a inne w lewo. Skręcenie płaszczyzny polaryzacji tłumaczymy tym, że światło spolaryzowane liniowo uważać można za nałożenie dwóch spójnych kołowo spolaryzowanych drgań, o równych okresach i amplitudach, lecz przeciwnych zwrotach ( prawoskrętnie i lewoskrętnie). Zjawisko to nosi nazwę dwójłomności kołowej. Obie składowe rozchodzą się z różnymi prędkościami, w wyniku czego wytwarza się między nimi różnica faz. Przy wyjściu z ciała te składowe dodają się i wypadkowa, chociaż nadal spolaryzowana liniowo, ma już inny azymut polaryzacji. Jeśli znane są oba współczynniki załamania i długość przebytej przez światło w danym ośrodku drogi l, różnicę faz δ można obliczyć na podstawie wzoru

gdzie n - różnica współczynników załamania, λ - długość fali światła. Kąt skręcenia ϕ stanowi połowę różnicy faz, ϕ=δ/2.

W przypadku roztworów, że kąt skręcenia ϕ jest proporcjonalny do długości l warstwy roztworu oraz do jego stężenia c. Tę zależność zdefiniowana jest prawem Biota :

gdzie K - współczynnik proporcjonalności zależny od:

1. rodzaju substancji rozpuszczonej

2. rodzaju rozpuszczalnika

3. długości światła

Ten współczynnik nosi nazwę skręcenia właściwego; równe liczbowo kątowi skręcenia na jednostkę stężenia [g*dm^-3] i na jednostkę długości warstwy roztworu [dm]

Przyrządy służące do pomiaru kąta skręcenia płaszczyzny polaryzacji nazwane są polarymetrami. Te z nich, które stosuje się do roztworów cukru noszą nazwę sacharymetrów

Światło spolaryzowane liniowo możemy zbadać za pomocą polaryzatora, zwanego w tym przypadku analizatorem. Obracając analizator wokół osi biegu wiązki światła spolaryzowanego, stwierdzimy rozjaśnienia pola widzenia względnie całkowite zaciemnienia. W przypadku zaciemnienia mamy pewność, że płaszczyzna polaryzacji analizatora jest prostopadła do płaszczyzny polaryzacji światła analizowanego. Do analizy światła spolaryzowanego eliptycznie potrzeba ćwierćfalówkę. Zamienia ona światło spolaryzowane eliptycznie na światło spolaryzowane liniowo. Jednak w tym przypadku półosie elipsy spolaryzowanego światła muszą być równoległe do azymutów ćwierćfalówki. W tym celu należy zbadać za pomocą analizatora kierunki półosi elipsy. Kierunek płaszczyzny polaryzacji analizatora wtedy, gdy przepuszcza on maksimum lub minimum światła, jest równoległy do odpowiedniej elipsy. Gdy azymuty ćwierćfalówki są równoległe do półosi, wtedy światło przechodzące zyskuje dodatkową różnicę faz równą π/2 lub (3/2)π, co łącznie z różnicą istniejącą w świetle spolaryzowanym eliptycznie daje całkowitą wielokrotność π i daje w wyniku drgania spolaryzowane liniowo.

---