AKADEMIA ROLNICZA ROK STUDIÓW II

W KRAKOWIE GRUPA 4b

KATEDRA GOSPODARKI WODNEJ

I OCHRONY WÓD

ĆWICZENIE NR 7

Obliczenie prawdopodobieństwa wystąpienia przepływów minimalnych dla profilu Klęczany na rzece Ropie metodą Gumbela.

Ćwiczenie zawiera :

1. Seria obserwacyjna przepływów minimalnych rocznych z wielolecia 1966-1983 dla rzeki
Ropy w profilu Klęczany.

2. Statystyczny ciąg rozdzielczy przepływów minimalnych rocznych w profilu Klęczany na
rzece Ropie.

3. Obliczenie charakterystyk ciągu.

4. Tabelaryczne zestawienie obliczeń krzywej kumulacyjnej prawdopodobieństwa

wystąpienia przepływów minimalnych na rzece Ropie.

5. Wykres krzywej kumulacyjnej prawdopodobieństwa wystąpienia przepływów
minimalnych.

6. Sprawdzenie zgodności krzywej empirycznej z przyjętym typem rozkładu testem
Kołmogorowa.

ROK AKADEMICKI 1998/99 STANISŁAW ZAJĄC

1. Seria obserwacyjna przepływów minimalnych rocznych

z wielolecia 1966-83 dla rzeki Ropy w profilu wodowskazowym Klęczany.

L.p.	Data	Qmin [ m^3/s ]
	2.XI.1983	0,58
	8.X.1982	0,52
	28.V.1981	1,60
	23.I.1980	1,24
	7.XII.1979	1,07
	4.VIII.1978	0,70
	6.IX.1977	0,70
	27.XI.1976	0,57
	1.X.1975	0,80
	5.XI.1974	0,70
	29.VIII.1973	0,70
	3.XI.1972	0,82
	21.IX.1971	0,60
	2.I.1970	0,93
	8.VIII.1969	0,35
	5.VII.1968	0,70
	9.IX.1967	0,80
	17.XI.1966	0,64

2. Statystyczny ciąg rozdzielczy przepływów

minimalnych rocznych.

L.p.	Qmin [ m^3/s ]	Qmin^2 [ m^3/s ]	p%	p′%
	1,60	2,56	5,26	94,74
	1,24	1,54	10,53	89,47
	1,07	1,14	15,79	84,21
	0,93	0,86	21,05	78,95
	0,82	0,67	26,32	73,68
	0,80	0,64	31,58	68,42
	0,80	0,64	36,84	63,16
	0,70	0,49	42,11	57,89
	0,70	0,49	47,37	52,63
	0,70	0,49	52,63	47,37
	0,70	0,49	57,89	42,11
	0,70	0,49	63,16	36,84
	0,64	0,41	68,42	31,58
	0,60	0,36	73,68	26,32
	0,58	0,34	78,95	21,05
	0,57	0,32	84,21	15,79
	0,52	0,27	89,47	10,53
	0,35	0,12	94,74	5,26
∑	14,02	12,33

wg. Weibulla

p′% = 100 - p%

gdzie

m - kolejny wyraz ciągu

N - liczba wyrazów ciągu

3. Określenie charakterystyk ciągu.

1) wartość średnia
= 0,78 m³/s

2) odchylenie średnie s=
= 0,29 m³/s

3) wartość najniższa zaobserwowana x₁= 0,35 m³/s

4) ocena funkcji testowej

t(λ, N)=
1,4873

5) określenie wartości parametru λ dla obliczonej wartości t(λ, N) równej 1,4873

i liczebności N =18

λ = 0,48

6) ocena parametru λ k =
k=
= 2,08

7) dolne ograniczenie ciągu ε

ε = x₁ -
0,21 m³/s

8) charakterystyczny przepływ minimalny

wartość funkcji Γ(1+
) dla
=0,48 wynosi 0,88575

θ =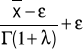
= 0,85 m³/s

4. Tabelaryczne zestawienie obliczeń krzywej kumulacyjnej prawdopodobieństwa wystąpienia przepływów minimalnych.

Q_{min p%} = ε + (θ - ε) e^λyp′

p'%	p%	yp'	λyp'	e^λ^yp'	(θ - ε)e^λ^yp'	Qmin p'%
0,1	99,9	-6,9178	-3,3205	0,0361	0,0233	0,2306
0,2	99,8	-6,2131	-2,9823	0,0507	0,0327	0,2399
0,5	99,5	-5,2943	-2,5413	0,0788	0,0508	0,2581
1	99	-4,6013	-2,2086	0,1099	0,0709	0,2781
2	98	-3,9024	-1,8732	0,1536	0,0992	0,3064
5	95	-2,97	-1,4256	0,2404	0,1551	0,3624
10	90	-2,2503	-1,0801	0,3395	0,2191	0,4264
25	75	-1,2459	-0,5980	0,5499	0,3549	0,5621
50	50	-0,3665	-0,1759	0,8387	0,5413	0,7485
80	20	0,4759	0,2284	1,2566	0,8110	1,0182
90	10	0,834	0,4003	1,4923	0,9631	1,1703
95	5	1,0972	0,5267	1,6933	1,0928	1,3000
99	1	1,5272	0,7331	2,0814	1,3433	1,5506

6. Sprawdzenie zgodności krzywej empirycznej
z przyjętym typem rozkładu testem Kołmogorowa.

D_max = maxp'(m, N)% - p'%<

gdzie:

p'(m, N)% - prawdopodobieństwo empiryczne

p'% - prawdopodobieństwo teoretyczne

D_max = 58%-42%<

P'(m, N)% =58 %

P'% = 42%

D_max = 16 < 32,1

Brak podstaw do odrzucenia przyjętego typu rozkładu.

---