Zadanie 1 (problem diety). Hodowca może kupić 2 rodzaje P1 i P2 gotowych pokarmów zawierających dwa główne składniki: wapń i fosfor. Zawartość tych składników w 1 kg pokarmu oraz cena 1 kg pokarmu są przedstawione w tabeli.

	Zawartość (dkg/kg)		Cena (zł/kg)
	Ca	P
P1	10	30	12
P2	15	20	15

Pies może zjeść w ciągu dnia maksymalnie 2 kg pokarmu. Zbudować model pozwalający ustalić wielkość dziennej konsumpcji obu pokarmów, tak aby łączny koszt dziennej diety był jak najmniejszy, zaś pies otrzymał co najmniej 15 dkg wapnia i 30 dkg fosforu.

1. Rozwiązać zadanie metodą graficzną.

2. Podać zakres zmienności ceny jednostkowej pokarmu P1.

3. Podać zakres zmienności ceny jednostkowej pokarmu P2.

4. O ile może wzrosnąć cena jednostkowa pokarmu P1, aby wyznaczone dla danych wyjściowych rozwiązanie pozostało rozwiązaniem optymalnym? O ile zmienią się wówczas koszty związane z dzienną dietą psa?

5. Czy wyznaczone rozwiązanie pozostanie optymalne, jeśli cena pokarmu P2 spadnie do 10 zł za kilogram? O ile mniej zapłaci wtedy hodowca?

6. Jak bardzo musiałaby wzrosnąć cena pokarmu P1, aby hodowca przestał go kupować?

7. Jak bardzo musiałaby spaść cena pokarmu P2, aby hodowcy opłacało się kupować tylko ten pokarm?

8. Cena pokarmu P1 spadła do 10 zł/kg. Co może zrobić hodowca?

9. Czy spadek minimalnego zapotrzebowania na wapń do 10 dkg dziennie spowoduje zmianę optymalnej diety?

10. Czy zmiana ograniczenia na dzienną rację pokarmu dla psa (obecnie 2 kg) wywoła zmianę kosztów optymalnej diety?

11. z powodu przejściowych trudności z zaopatrzeniem hodowca nie jest w stanie nabyć dziennie więcej niż 1 kg pokarmu P1. Czy wyznaczona poprzednio dieta optymalna pozostanie niezmieniona? A gdyby to było 0,5kg?

Zadanie 2. Dane jest zadanie optymalizacyjne:

przy warunkach:

Dla jakich wartości parametru α∈R zadanie to

1. jest sprzeczne,

2. ma dokładnie jedno rozwiązanie optymalne,

3. ma nieskończenie wiele rozwiązań optymalnych

4. nie ma rozwiązań optymalnych, gdyż funkcja celu jest nieograniczona z góry na zbiorze rozwiązań dopuszczalnych.

Zadanie 3 (plan produkcji). Zakład wytwarza dwa produkty A i B. W procesie produkcyjnym wykorzystywane są różne surowce, półprodukty, siła robocza i maszyny. Rynek surowców i półproduktów jest ustabilizowany w tym sensie, że są one do nabycia w każdej chwili i ilości, a ich ceny są stabilne. Załoga zatrudniona w dziale produkcyjnym liczy 50 osób. Przy ustalaniu planu produkcji kierownictwo zakładu musi wziąć pod uwagę następujące ograniczenia:

• Dzień pracy w dziale produkcyjnym trwa 6 godzin

• Technologia wymaga, aby na pewnym etapie półprodukty były przetworzone przez
  urządzenia, które nie mogą pracować dłużej niż 5 godzin dziennie. Zakład posiada 36
  takich urządzeń.

• Umowy z kontrahentami opiewają na dostawy 2 tys. jednostek produktu A oraz 8 tys.
  jednostek produktu B dziennie. Niedotrzymanie tych umów jest dla zakładu zbyt kosztowne.

• Nie występują inne ograniczenia typu czasowego ani ilościowego.

W tabeli podane są pewne ilościowe charakterystyki procesu produkcyjnego w tym zakładzie:

Produkt	Wydajność pracy (l.prod./rbgodz.)	Przepustowość urządzeń (l. prod./godz.)
A	100	80
B	80	160

Ponadto, w wyniku obliczeń ustalono, że jednostkowy koszt produkcji wynosi 85 zł w przypadku produktu A i 82 zł w przypadku produktu B. Koszty stałe zostały oszacowane na poziomie 50 tys. zł dziennie. Zakład jest w stanie sprzedać dowolną ilość jednego i drugiego produktu, a ich ceny jednostkowe są ustabilizowane i wynoszą 100 i 96 zł odpowiednio dla produktu A i B.

1. Który z podanych planów produkcji jest planem dopuszczalnym dziennej produkcji?

Plan 1: po 2000 jednostek każdego produktu, A i B.

Plan 2: 3000 jednostek produktu A i 10000 jednostek produktu B.

Plan 3: 5000 jednostek produktu A i 8000 jednostek produktu B.

Plan 4: po 10000 jednostek każdego produktu, A i B.

Plan 5: 10000 jednostek produktu A i 8000 jednostek produktu B.

2. Który z dopuszczalnych planów produkcji z punktu a. nie jest planem optymalnym?

3. Zbudować zadanie optymalizacyjne pozwalające wyznaczyć plan dziennej produkcji maksymalizujący łączny zysk z produkcji.

Rozwiązać zadanie PL z punktu c. Wskazać warunki napięte w rozwiązaniu optymalnym zadania.

Odp.: a. B, C, E, b. B, C c. RO= (4000 20 800), napięte: ludzie i maszyny

Zadanie domowe 1. Dane jest zadanie optymalizacyjne:

przy warunkach:

Dla jakich wartości parametru α∈R zadanie to

1. jest sprzeczne,

2. ma dokładnie jedno rozwiązanie optymalne,

3. ma nieskończenie wiele rozwiązań optymalnych,

4. nie ma rozwiązań optymalnych, gdyż funkcja celu jest nieograniczona z góry na zbiorze rozwiązań dopuszczalnych.

Zadanie domowe 2. Dany jest zbiór D decyzji dopuszczalnych:

.

Wyznaczyć zbiór decyzji optymalnych D_opt następujących zadań PL:

1. 
   przy warunkach (x₁, x₂)∈D

2. 
   przy warunkach (x₁, x₂)∈D

3. 
   przy warunkach (x₁, x₂)∈D

4. 
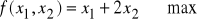
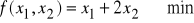
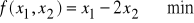
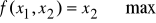
   przy warunkach (x₁, x₂)∈D

W każdym z tych zadań wskaż wszystkie te warunki ograniczające, których usunięcie nie spowoduje zmiany zbioru D_opt.

---