Rok akademicki 1997/98 |
LABORATORIUM FIZYCZNE |
|||
Ćwiczenie nr 55 |
IDENTYFIKACJA PIERWIASTKA PROMIENIOTWÓRCZEGO PRZEZ WYZNACZENIE GÓRNEJ GRANICY WIDMA BETA
|
|||
Wydział Mechaniczny IZK grupa K05 B |
Wykonał: Robert Cincio |
|||
Data wykonania |
OCENA |
DATA |
PODPIS |
|
12.03.98 |
T |
|
|
|
|
S |
|
|
|
1. Część teoretyczna
Elektrony i inne cząstki naładowane tracą energię podczas ruchu w ośrodku materialnym. Do zliczania cząstek naładowanych, którym mimo strat energii w czasie przechodzenia przez środek materialny udało się przebić przez ten ośrodek służy licznik Geigera-Müllera. Licznik Geigera-Müllera jest to cylinder metalowy wypełniony gazem. Wzdłuż osi cylindra rozpięty jest metalowy drut, który ma względem ścianek potencjał dodatni około 1000V. Pojawienie się wewnątrz cylindra cząstki jonizującej powoduje powstanie w liczniku jonów, które są przyśpieszane przez pole elektryczne między drutem a cylindrem i wywołują z kolei dalszą jonizację. Bardzo wysoki wzrost liczby jonów powoduje wyładowanie. Za każdym razem, kiedy w liczniku wzbudza się wyładowanie, impuls prądu powstający w liczniku i wzmacniany do wymaganej wartości sygnalizuje pojawienie się w nim jednej cząstki.
Celem pomiaru było wyznaczenie zasięgu maksymalnego cząstek β w aluminium metodą całkowitego pochłaniania. Mierzoną wielkością była liczba impulsów zliczanych przez licznik Geigera-Müllera w czasie stu sekund. Na podstawie ilości cząstek naładowanych, które przeszły przez ośrodek materialny możemy wyznaczyć energię maksymalną cząstek β, a korzystając z wykresu zależności
![]()
możemy wyznaczyć rodzaj pierwiastka promieniotwórczego użytego w ćwiczeniu.
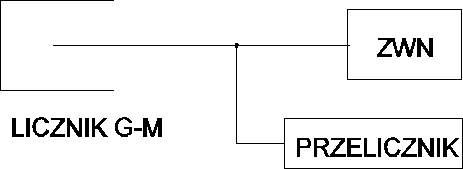
2. Schemat układu pomiarowego
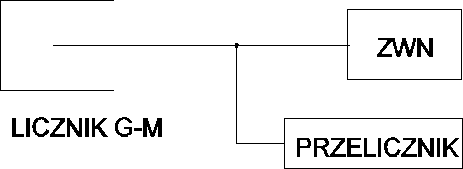
3. Dokładność pomiarów
W ćwiczeniu należy obliczyć błędy statystyczne dokonanych pomiarów. Aby te błędy były jak najmniejsze, serie pomiarów powinno wykonywać się wiele razy (w naszym przypadku 2 razy).
![]()
Błąd statystyczny:
Błędy pomiaru liczby zliczeń obliczamy za pomocą wzoru:
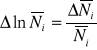
Wyniki obliczeń przedstawiono w tabeli.
4. Tabela pomiarowa
Lp. |
ni
|
_ ni
|
_ Ni
|
Ri
|
_
ΔNi=± |
_ lnNi |
_ Δ(lnNi) |
1 |
182,190 |
186 |
111,6 |
0 |
10,56 |
4,71 |
0,09 |
2 |
132,104 |
118 |
70,8 |
20,25 |
8,41 |
4,26 |
0,12 |
3 |
94,103 |
98,5 |
59,1 |
40,5 |
7,68 |
4,08 |
0,13 |
4 |
85,66 |
75,5 |
45,3 |
60,75 |
6,73 |
3,81 |
0,15 |
5 |
61,49 |
55 |
33 |
81 |
5,74 |
3,50 |
0,17 |
6 |
59,50 |
54,5 |
32,7 |
101,25 |
5,71 |
3,49 |
0,17 |
7 |
51,45 |
48 |
28,8 |
121,5 |
5,36 |
3,36 |
0,19 |
8 |
43,37 |
40 |
24 |
141,75 |
4,89 |
3,18 |
0,20 |
9 |
36,47 |
41,5 |
24,9 |
162 |
4,98 |
3,21 |
0,20 |
10 |
48,38 |
43 |
25,8 |
182,25 |
5,07 |
3,25 |
0,20 |
11 |
39,34 |
36,5 |
21,9 |
202,5 |
4,67 |
3,09 |
0,21 |
12 |
39,34 |
36,5 |
21,9 |
tło |
4,67 |
3,09 |
0,21 |
5. Wykres
Wykres lnNi = f(Ri) dołączono na końcu sprawozdania.
6. Wnioski
Zasięg maksymalny cząstek β w aluminium określamy z wykresu zależności lnNi = f(Ri) poprzez ekstrapolację krzywej absorpcji do tła. Maksymalną energię cząstek beta możemy wyznaczyć z zależności Rmax = f(Eβmax), a stąd możemy zidentyfikować pierwiastek promieniotwórczy.
Zasięg maksymalny cząstek β wynosi: Rmax = 110 mg/cm2, co w przybliżeniu odpowiada pierwiastkowi 185W o energii maksymalnej Eβmax = 0,430.
Jak wynika z umieszczonych w tabelce pomiarów, promieniowanie tła czyli blaszek aluminiowych jest równe promieniowaniu pierwiastka osłoniętego tymi blaszkami. Widać więc, że aluminium całkowicie pochłania promieniowanie cząstek β, ale jest to zależne od jego grubości
![]()
![]()
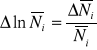
Wyszukiwarka
Podobne podstrony:
sprawozdanie fiza 6 (cw. 50), 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza,
FIZA 52 NASZA, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, fiza, spr, fizyka, La
Sprawozdanie fiza 5 (ćw.71), 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza,
Fiza 23 Dzikoos`a, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, fiza, spr, fizyka
Fiza 72 Nasza, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza,
Fiza 55 moje, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza, F
WYKRES73, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
Fizzad2, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
STOS-EM, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
Fizyka21, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
FizWyks2, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
065S~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
FizPrad, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
051C~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
SUCHY73, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
062C~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
065A~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
więcej podobnych podstron