Rok akademicki 1997/98 |
LABORATORIUM FIZYCZNE |
|||
Ćwiczenie nr 72 |
ZJAWISKO HALLA
|
|||
Wydział Mechaniczny IZK grupa K05 B |
Wykonali: Robert Cincio, Marcin Majka |
|||
Data wykonania |
OCENA |
DATA |
PODPIS |
|
2.04.98 |
T |
|
|
|
|
S |
|
|
|
Część teoretyczna
Celem kolejnego naszego ćwiczenia było wyznaczenie stałej Halla dla półprzewodnika oraz wyznaczenie koncentracji i ruchliwości nośnika. Zjawisko Halla to zjawisko galwanomagnetyczne polegające na pojawianiu się napięcia (tzw. napięcia Halla UH) w płytce półprzewodnika lub metalu, przez którą płynie prąd elektryczny, umieszczonej w prostopadłym do kierunku prądu polu magnetycznym. Napięcie Halla pojawia się w kierunku prostopadłym zarówno do kierunku pola magnetycznego, jak i prądu
gdzie:
RH - stała Halla,
B - indukcja pola magnetycznego,
j - gęstość prądu w płytce,
a - odległość między punktami.
Stała Halla zależy od koncentracji, rodzaju i ruchliwości nośników ładunku. Jeśli w przewodnictwie elektrycznym dominuje jeden rodzaj nośników (dziury lub elektrony), to jest ona odwrotnie proporcjonalna do ich koncentracji. Pomiar napięcia Halla jest jedną z podstawowych metod badania właściwości nośników ładunku, zwłaszcza w półprzewodnikach. Na podstawie znaku napięcia Halla można określić jaki rodzaj nośników (dziury czy elektrony) dominuje w przewodnictwie. Pomiar temperaturowej zależności napięcia Halla oraz konduktancji w półprzewodnikach umożliwia określenie właściwości domieszek (ich koncentracji, rodzaju, energii wiązania), mechanizmów rozpraszania nośników ładunku oraz dostarcza ważnych informacji o strukturze pasmowej półprzewodników.
Koncentracja nośników
Ruchliwość nośników
gdzie:
V - prędkość elektronów
E - natężenie pola.
Schemat pomiarowy
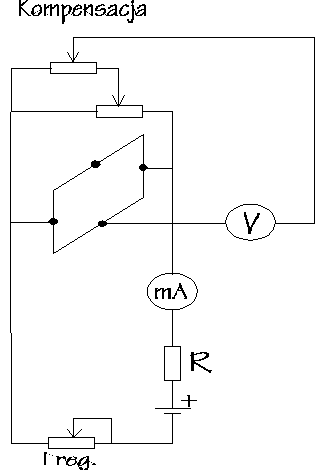
Przebieg ćwiczenia
Po uruchomieniu układu, zwiększano natężenie prądu i odczytywano na woltomierzu napięcie UH+ i UH-
W ćwiczeniu wykorzystano próbki monokryształu germanu, typu „n” o parametrach podanych poniżej.
Lp. |
wielkość |
Wartość |
Błąd max. |
Jednostka |
1 |
l |
5 |
0.1 |
mm |
2 |
a |
3 |
0.1 |
mm |
3 |
b |
2 |
0.1 |
μm |
4 |
ρ |
1,5x10-3 |
- |
Ωm |
5 |
β |
160 |
7.5 |
mT |
Błąd pomiaru stałej Halla oblicza się za pomocą różniczki logarytmicznej oblicza się za pomocą wzoru:
gdzie: 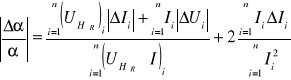
ΔUi i ΔIi - błędy poszczególnych pomiarów napięcia i natężenia prądu.
Digital Voltmeter Type V541 ΔU=±0,05% wartości mierzonej + 0,01 mV.
Klasa dokładności miliamperomierza użytego w ćwiczeniu wynosi 0,5 , a zakres pomiarowy wynosił 30 mA.
Przykładowe obliczenia błędów
Obliczenie współczynnika kierunkowego α prostej UH=f(I).
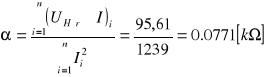
Obliczamy stałą Halla:
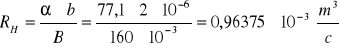
Obliczamy koncentrację nośników (elektronów) n:
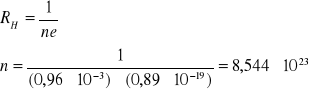
Obliczamy ruchliwość nośników ładunku ze wzoru:
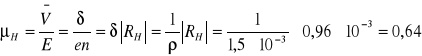
gdzie:
δ - przewodność elektryczna właściwa materiału próbki,
ρ - opór właściwy materiału ( germanu ).
Tabele pomiarowe
Lp. |
I [mA] |
-UH [mV] |
UH [mV] |
UHśr [mV] |
UHśr ⋅ I [mV ⋅ mA] |
1 |
2 |
0,14 |
0,14 |
0,14 |
0,28 |
2 |
3 |
0,22 |
0,22 |
0,22 |
0,66 |
3 |
4 |
0,30 |
0,29 |
0,295 |
1,18 |
4 |
5 |
0,38 |
0,36 |
0,37 |
1,85 |
5 |
6 |
0,46 |
0,44 |
0,45 |
2,7 |
6 |
7 |
0,54 |
0,52 |
0,53 |
3,71 |
7 |
8 |
0,63 |
0,60 |
0,615 |
4,92 |
8 |
9 |
0,72 |
0,69 |
0,705 |
6,345 |
9 |
10 |
0,80 |
0,76 |
0,78 |
7,8 |
10 |
11 |
0,87 |
0,85 |
0,86 |
9,46 |
11 |
12 |
0,95 |
0,92 |
0,935 |
11,22 |
12 |
13 |
1,04 |
1,01 |
1,025 |
13,325 |
13 |
14 |
1,08 |
1,05 |
1,065 |
14,91 |
14 |
15 |
1,15 |
1,15 |
1,15 |
17,25 |
Δ |
0,15 |
0,67285 |
0,65285 |
− |
− |
Σ |
− |
− |
− |
9,14 |
95,61 |
![]()
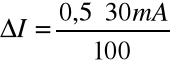
Lp. |
I2 [mA2] |
UHśr⋅ΔI [mV⋅mA] |
I⋅ΔUHśr [mA⋅mV] |
I⋅ΔI [mA2] |
UH(teoretyczne) [mV] |
1 |
4 |
0,02 |
0,034 |
0,30 |
0,1522 |
2 |
9 |
0,03 |
0,063 |
0,45 |
0,2283 |
3 |
16 |
0,04 |
0,099 |
0,60 |
0,3044 |
4 |
25 |
0,06 |
0,143 |
0,75 |
0,3805 |
5 |
36 |
0,07 |
0,195 |
0,90 |
0,4566 |
6 |
49 |
0,08 |
0,256 |
1,05 |
0,5327 |
7 |
64 |
0,09 |
0,326 |
1,20 |
0,6088 |
8 |
81 |
0,11 |
0,407 |
1,35 |
0,6849 |
9 |
100 |
0,12 |
0,490 |
1,50 |
0,761 |
10 |
121 |
0,13 |
0,583 |
1,65 |
0,8371 |
11 |
144 |
0,14 |
0,681 |
1,80 |
0,9132 |
12 |
169 |
0,15 |
0,796 |
1,95 |
0,9893 |
13 |
196 |
0,16 |
0,886 |
2,10 |
1,0654 |
14 |
225 |
0,17 |
1,013 |
2,25 |
1,1415 |
Σ |
1239 |
1,37 |
5,971 |
17,85 |
− |
6. Wnioski
Wraz ze wzrostem prądu płynącego przez przewodnik lub półprzewodnik napięcie Halla wzrasta. Za pomocą zjawiska Halla możemy mierzyć wielkość indukcji magnetycznej. Zjawisko to obserwuje się we wszystkich przewodnikach i półprzewodnikach niezależnie od materiału, z jakiego są wykonane. Zjawisko Halla zastosowano do budowy tzw. hallotronów. Hallotron jest to bezzłączowy przyrząd półprzewodnikowy stosowany do pomiaru pola magnetycznego, prądu, mocy itp. Wykres dołączony jest na papierze milimetrowym.
![]()
![]()
Wyszukiwarka
Podobne podstrony:
FIZA 52 NASZA, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, fiza, spr, fizyka, La
Fiza 62 Nasza, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Labolatorium Fizyki, 62 Oporn
Fiza 55 dzika, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza,
sprawozdanie fiza 6 (cw. 50), 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza,
Fiza 73 Nasza, 1 STUDIA - Informatyka Politechnika Koszalińska, finish, Fizyka, fiza, spr, fizyka, L
Sprawozdanie fiza 5 (ćw.71), 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza,
Fiza 55 moje, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, sprawka od Mateusza, F
Fiza 23 Dzikoos`a, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, Fizyka, fiza, spr, fizyka
Fiza 71 Nasza, 1 STUDIA - Informatyka Politechnika Koszalińska, finish, Fizyka, sprawka od Mateusza,
WYKRES73, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
Fizzad2, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
STOS-EM, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
Fizyka21, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
FizWyks2, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
065S~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
FizPrad, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
051C~1, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
więcej podobnych podstron