Model regresji liniowej dwóch zmiennych

Model ten ma postać:

(1)

gdzie:

Y - zmienna objaśniana,

X - zmienna objaśniająca,

- parametry funkcji regresji,

U - składnik losowy, który w modelu jest jedynym źródłem losowości Y.

Prosty model regresji liniowej składa się ze składnika nielosowego (systematycznego) i błędu losowego.

Składnik systematyczny przedstawia średnie warunkowe wartości zmiennej Y przy danym X, co można zapisać następująco:

Jest to tzw. funkcja regresji pierwszego rodzaju.

Można również zdefiniować funkcję regresji pierwszego rodzaju w postaci:

Ogólnie biorąc prosty model regresji liniowej „funkcjonuje” przy kilku założeniach.

1. Związek między zmiennymi X i Y jest liniowy.

2. Wartości zmiennej objaśniającej X są ustalone, czyli nielosowe.

3. Losowość wartości zmiennej Y pochodzi tylko i wyłącznie ze składnika losowego.

4. Składnik losowy ma rozkład normalny (jakkolwiek nie jest to konieczne) o średniej 0 i stałej wariancji.

5. Realizacje składnika losowego nie są ze sobą wzajemnie skorelowane.

W rezultacie oszacowaną funkcją regresji Y względem X jest funkcja:

(2)

gdzie:

− oceny parametrów funkcji regresji typu (1),

U − reszty modelu regresji (2), które reprezentują realizacje składnika losowego modelu (1).

Funkcję regresji typu (2) określa się mianem funkcji regresji drugiego rodzaju.

Estymacja parametrów funkcji regresji

Parametry funkcji regresji muszą zostać oszacowane. W tym celu trzeba zastosować określoną metodę estymacji.

W praktyce najczęściej stosowaną metodą jest klasyczna metoda najmniejszych kwadratów. Metoda ta pozwala na „znalezienie” takiej funkcji regresji, która jest możliwie najlepiej dopasowana do wyników obserwacji. Wynika to z faktu, że parametry funkcji regresji są szacowane tak, by spełniony był warunek:

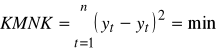
gdzie:

− wartości empiryczne zmiennej objaśnianej,

− wartości teoretyczne zmiennej objaśnianej, tj. obliczone na podstawie funkcji regresji.

Łatwo zauważyć, że kryterium najmniejszych kwadratów (KKMNK) wymaga, by suma kwadratów odchyleń wartości empirycznych zmiennej objaśnianej od wartości teoretycznych tej zmiennej była najmniejsza.

1

---