STATYSTYKA OPISOWA

WYKŁAD 2

WPROWADZENIE

Wyraz statystyka pochodzi od łacińskiego słowa status,

co oznacza stan, położenie. Statystyka to zbiór
metod służących pozyskiwaniu, prezentacji i analizie
danych oraz wyciąganiu wniosków . Inna definicja:
statystyka to nauka traktująca o metodach
ilościowych badania zjawisk masowych. Zjawisko
masowe

to

takie

zjawisko,

które badane w dużej masie zdarzeń wskazuje
właściwą sobie prawidłowość, jakiej nie można
zaobserwować
w pojedynczym przypadku. Przykłady zjawisk
masowych: spożycie pewnych artykułów na 1
mieszkańca,

urodzenia,

leczenie,

mierzenie

temperatury, ciśnienia itp.

Statystyka:

a) umożliwia dokładniejszy sposób opisu interesującej

nas rzeczywistości,

b) zmusza nas do dokładności i śmiałości w działaniu

i rozumowaniu,

c) umożliwia formułowanie uogólnień na podstawie

uzyskanych wyników analizy,

d) pozwala na przewidywanie rozwoju zjawisk

w przyszłości, czyli pobudzanie do prognoz,

e) dostarcza narzędzi do porządkowania informacji

o zjawiskach – a przez to pozwala na budowę ich

ogólnego obrazu,

f) dostarcza narzędzi do prowadzenia analizy

przyczyn kształtujących badane zjawiska i procesy,

a więc umożliwia dokonanie ich klasyfikacji na

czynniki systematyczne i przypadkowe.

Powstaje pytanie: dlaczego w zbiorze wielu zdarzeń

zachodzą prawidłowości statystyczne podczas, gdy

poszczególne zdarzenia są zróżnicowane? Otóż

każde

zjawisko

(ekonomicznej,

przyrodnicze,

socjologiczne itp.) kształtuje się pod wpływem

dwojakiego rodzaju przyczyn:

1.

głównych

(podstawowych,

typowych,

systematycznych).

2.

ubocznych (przypadkowych, indywidualne).

Ad 1) Przyczyny główne oddziałują na każde zjawisko

w sposób jednakowy, mają charakter wewnętrzny,

ich istota wypływa z charakteru zjawiska – działają w

ściśle określonym kierunku. Przyczyny te są wspólne

dla wszystkich jednostek badanej zbiorowości

zdarzeń (wpływ czynników głównych).

Ad 2) Przyczyny uboczne działają na każde

zjawisko w sposób odmienny. Wyrażają

zróżnicowanie osobnicze (wpływ czynnika losowego).

Ostatecznym celem stosowania tych

metod jest otrzymanie użytecznych
informacji na temat zjawiska, którego
dotyczą. Istotne jest, aby badania
statystyczne

były

zaplanowane

w sposób nie budzący zastrzeżeń. Ich
cel powinien być określony zrozumiale
i szczegółowo. Materiał statystyczne
powinien zaś być wiarygodny i
przejrzysty.

Cel badania jest możliwy do osiągnięcia

wówczas, gdy jednostki statystyczne
są precyzyjnie określone pod
względem:

- rzeczowym (przedmiot badań),
- przestrzennym (miejsce badań),
- czasowym (okres badań).

ZBIOROWOŚĆ I CECHY

STATYSTYCZNE

Zbiorowość statystyczna (populacja)

to zbiór dowolnych elementów
objętych badaniem statystycznym.
Wyodrębniona część zbiorowości nosi
nazwę próby statystycznej.
Elementy badanej zbiorowości
określane są mianem jednostek
statystycznych. Właściwości tych
jednostek nazywane są cechami
statystycznymi.

CECHY STATYSTYCZNE:

I.

STAŁE (wspólne wszystkim
jednostkom badanej zbiorowości).
Nie podlegają badaniu a jedynie
decydują o zaliczeniu jednostek do
określonej zbiorowości.

II. ZMIENNE (podlegają badaniom).

Cechy statystycznie zmienne:

ilościowe jakościowe

skokowe ciągłe

Badania statystyczne:

pełne częściowe

spisy rejestracja bieżąca

sprawozdawczość

Badania statystyczne:

ciągłe okresowe

doraźne

Metody prezentacji danych

statystycznych:

1. Szeregi statystyczne.
2. Tablice statystyczne.
3. Wykresy statystyczne.

Szeregi statystyczne

(ze względu na budowę):

proste szczegółowe rozdzielcze
Przykład szeregu prostego. Cecha

statystyczna: czas snu wyrażona w
godzinach. Wyniki obserwacji: 7, 8, 5, 6, 9,
8, 7, 7, 8, 7, 8, 5, 6, 9, 8, 7, 7, 9, 8, 7, 7, 8,
7, 8, 6, 9, 8, 7, 7, 8, 7, 8, 5, 6, 9

Przykład szeregu rozdzielczego

Obliczone wskaźniki struktury i liczebności kumulowane

Nr klasy

Czas

reakcji na

lek

(w

minutach)

Liczebnoś

ć

(n

i

)

Wskaźnik

struktury

(%)

Liczebnoś

ć

kumulowa

na

1
2
3
4

5
6
7

8-12

13-17
18-22
23-27

28-32
33-37
38-42

4

29
38
80

35

9
5

2,0

14.9
19,0
40,0

17,5

4,5
2,5

4

33
71

151

186
195
200

Razem

200

100,0

Nr klasy

Czas

reakcji na

lek

(w

minutach)

Liczebnoś

ć

(n

i

)

Wskaźnik

struktury

(%)

Liczebnoś

ć

kumulowa

na

1
2
3
4

5
6
7

8-12

13-17
18-22
23-27

28-32
33-37
38-42

4

29
38
80

35

9
5

2,0

14.9
19,0
40,0

17,5

4,5
2,5

4

33
71

151

186
195
200

Razem

200

100,0

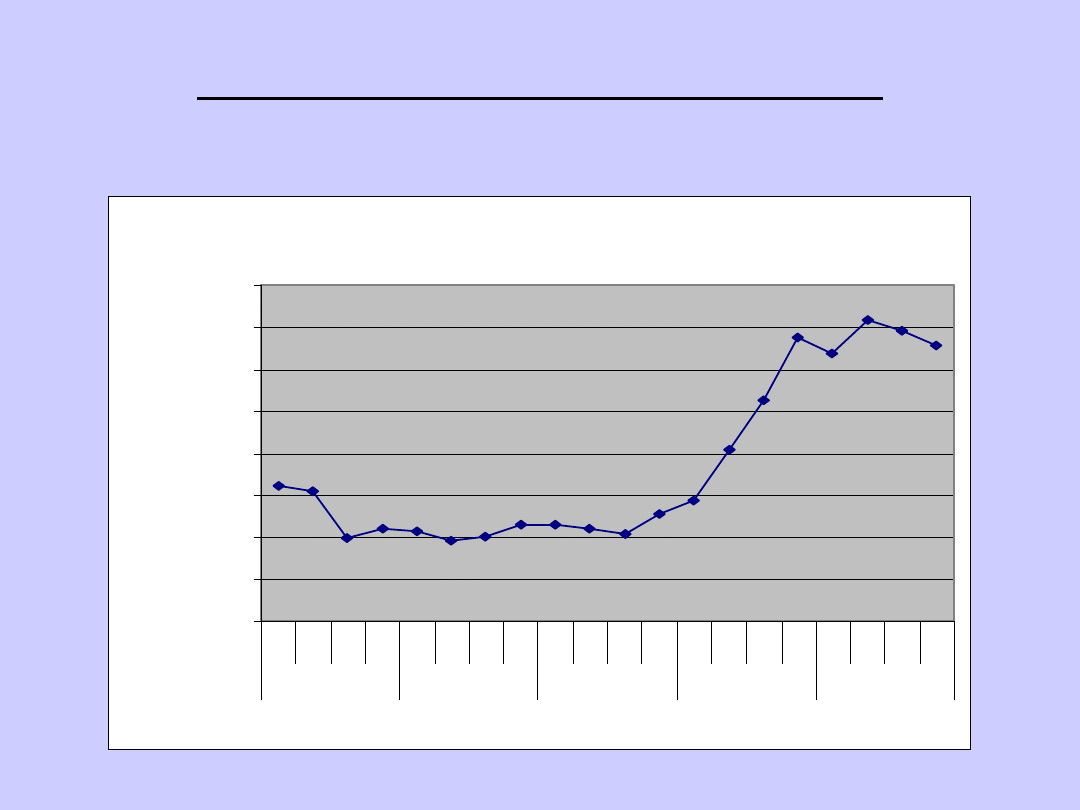
WYKRESY STATYSTYCZNE:

LINIOWY

Ceny akcji spółki Kęty

0,00

20,00

40,00

60,00

80,00

100,00

120,00

140,00

160,00

1k

w

2k

w

3k

w

4k

w

1k

w

2k

w

3k

w

4k

w

1k

w

2k

w

3k

w

4k

w

1k

w

2k

w

3k

w

4k

w

1k

w

2k

w

3k

w

4k

w

2000

2001

2002

2003

2004

kwartały

ce

n

a

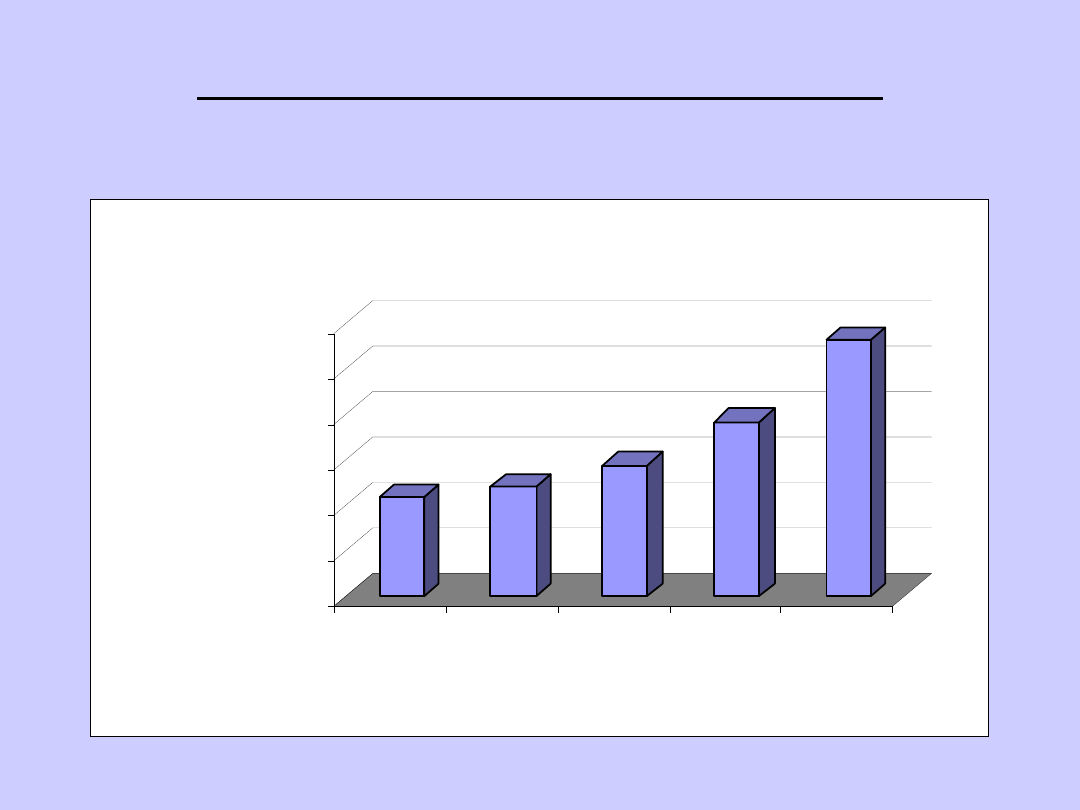
WYKRESY STATYSTYCZNE:

BRYŁOWY

434

481

576

768

1130

0

200

400

600

800

1000

1200

wartość

(mln PLN)

2000

2001

2002

2003

2004

lata

Przychody ze sprzedaży

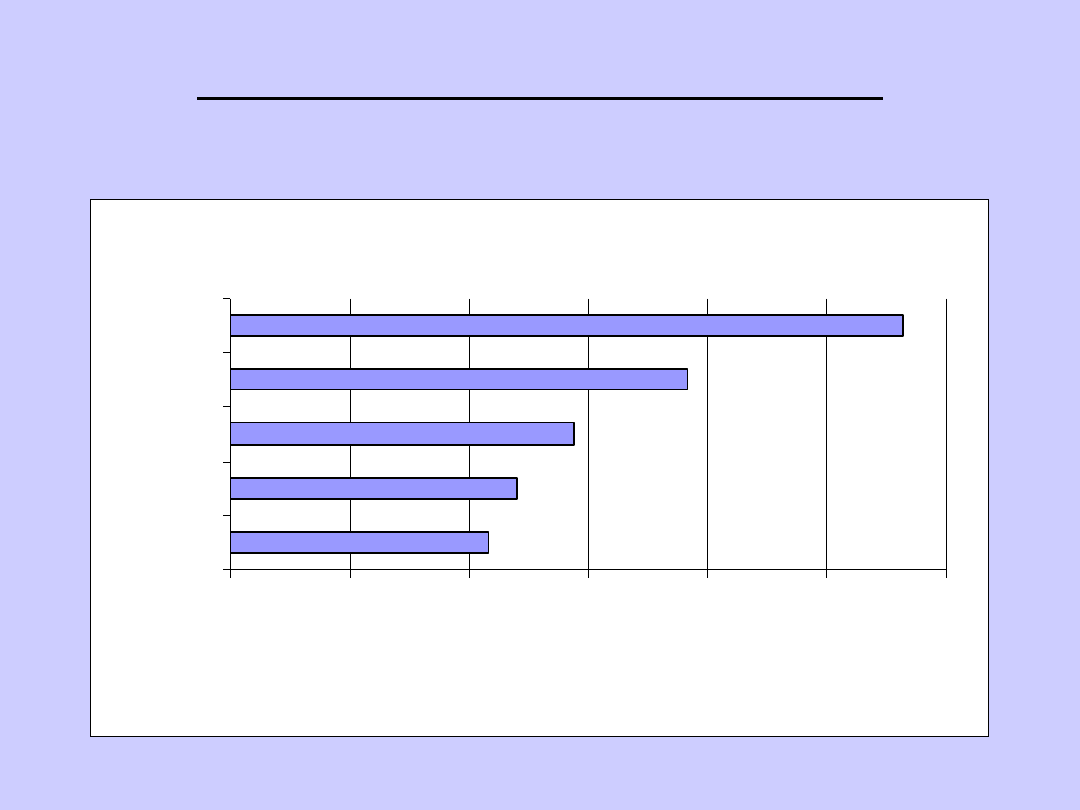
WYKRESY STATYSTYCZNE:

SŁUPKOWY

Przychody ze sprzedaży

434

481

576

768

1130

0

200

400

600

800

1000

1200

2000

2001

2002

2003

2004

lata

wartość

(mln PLN)

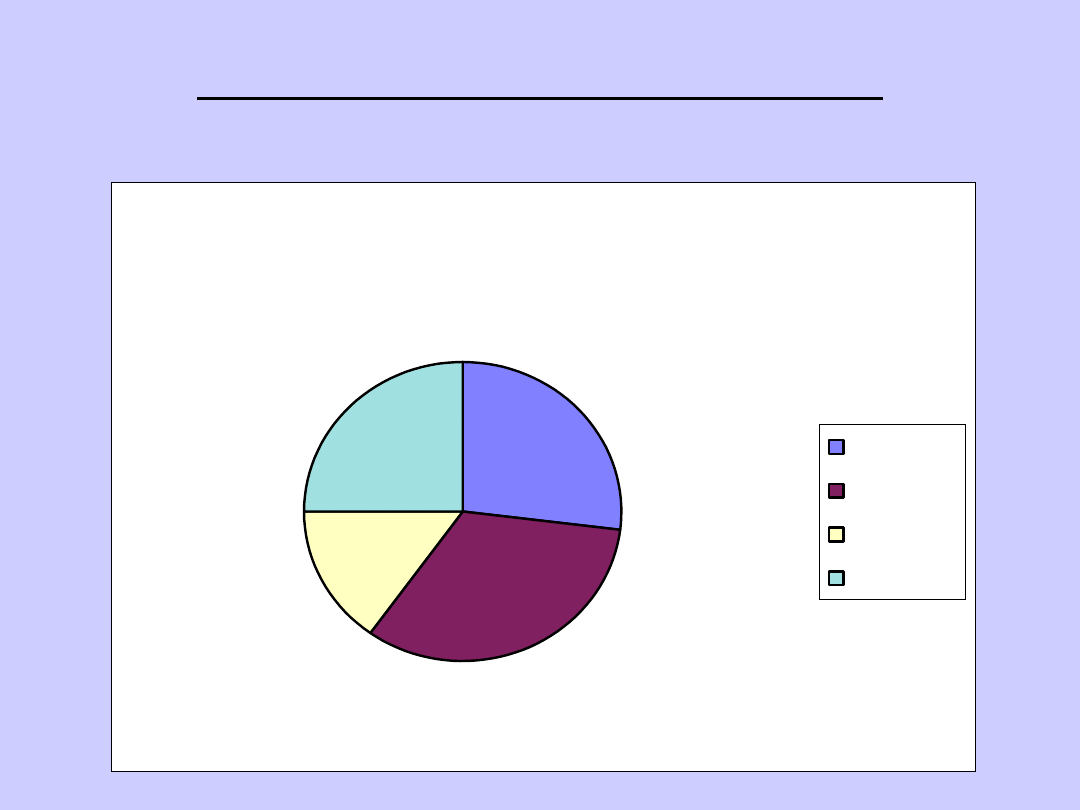
WYKRESY STATYSTYCZNE:

KOŁOWY

Udziały w rynku

27%

33%

15%

25%

Spółka A
Spólka B
Spółka C
Spółka D

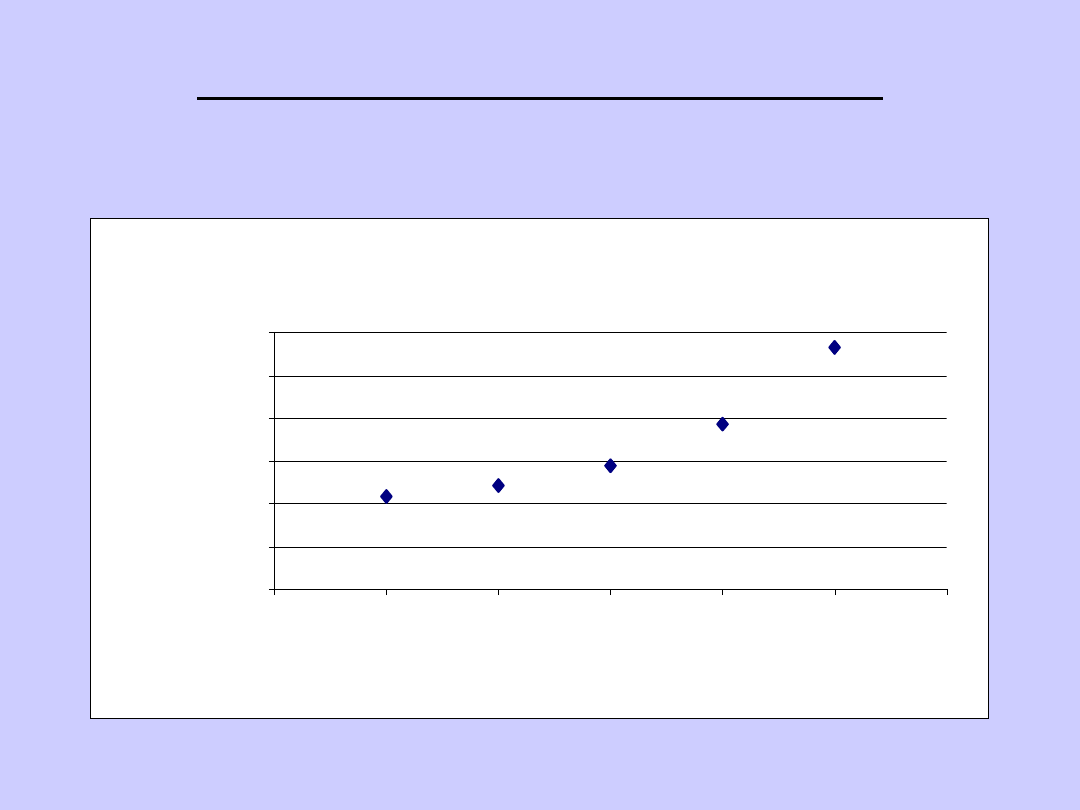
WYKRESY STATYSTYCZNE:

PUNKTOWY

Przychody ze sprzedaży

434

481

576

768

1130

0

200

400

600

800

1000

1200

1999

2000

2001

2002

2003

2004

2005

lata

wartość

(mln PLN)

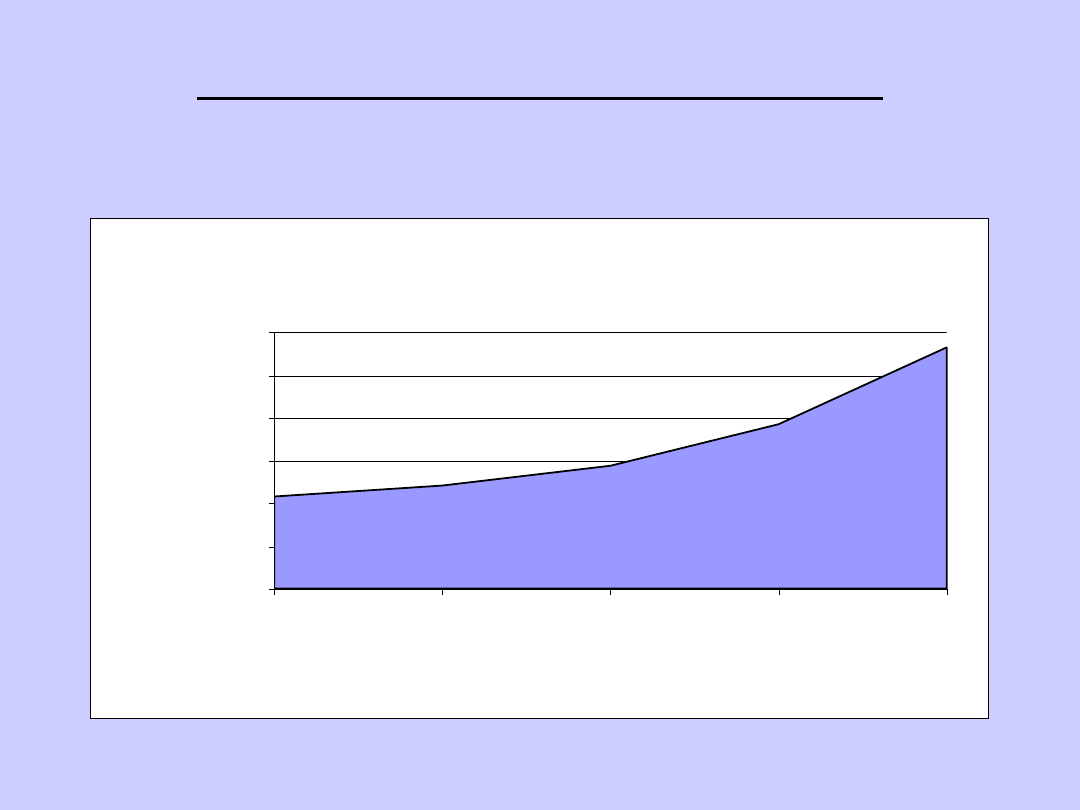
WYKRESY STATYSTYCZNE:

WARTSTWOWY

Przychody ze sprzedaży

434

481

576

768

1130

0

200

400

600

800

1000

1200

2000

2001

2002

2003

2004

lata

wartość

(mln PLN)

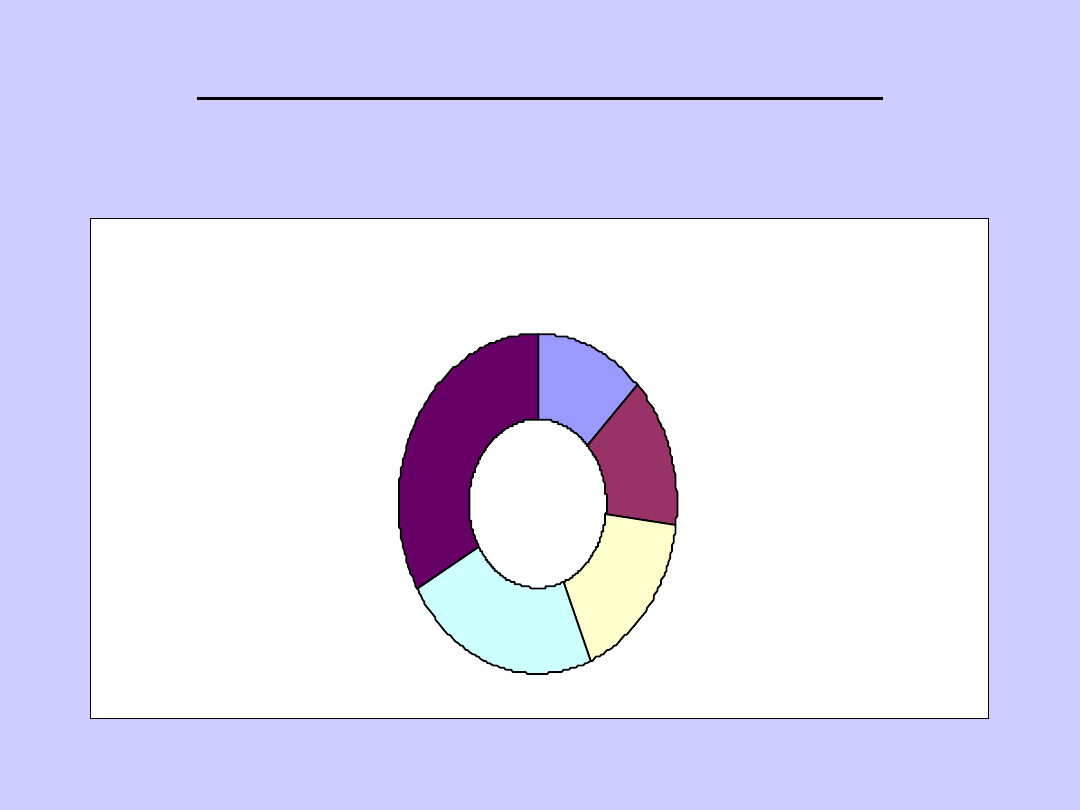
WYKRESY STATYSTYCZNE:

PIERŚCIENIOWY

Przychody ze sprzedaży

434

481

576

768

1130

ANALIZA STRUKTURY ZJAWISK

MASOWYCH

Rozkładem empirycznym określa się

przyporządkowanie poszczególnym
wartościom zmiennej x

i

odpowiadających im liczebności n

i

. W

określaniu rozkładu empirycznego zamiast
liczebności n

i

stosuje się częstości

względne określone wzorem:

przy czym:

n

n

w

i

i



n

n

k

i

i





1

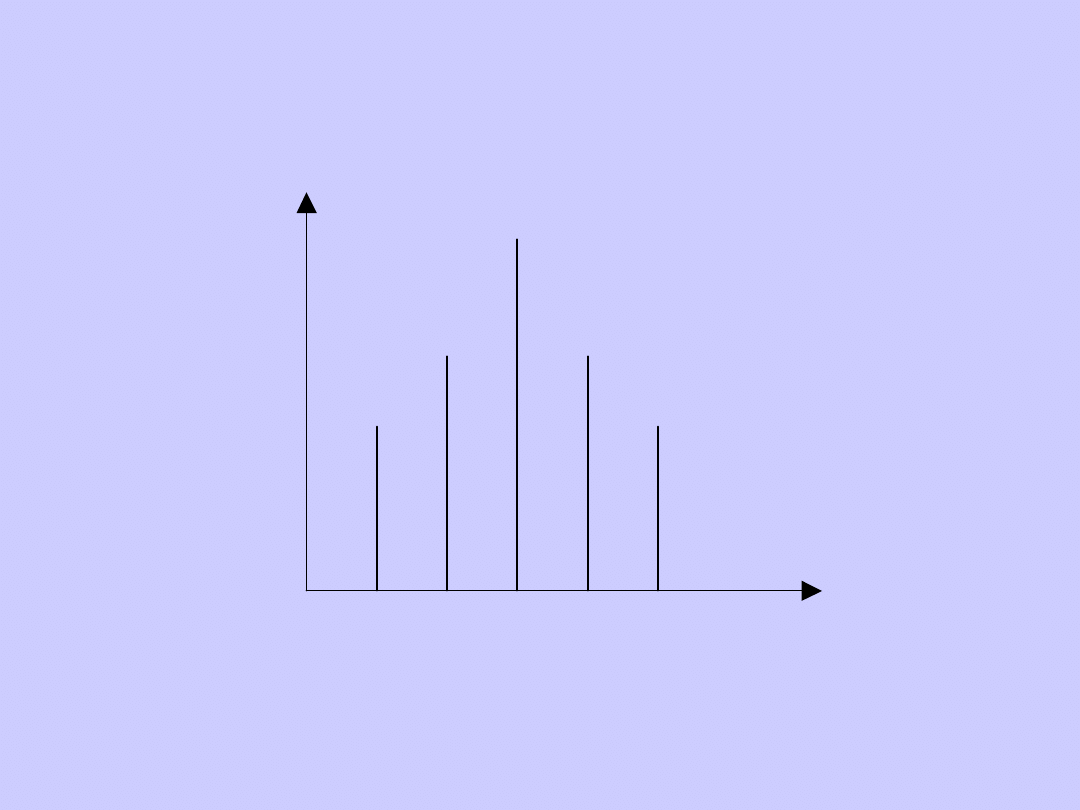
TYPY ROZKŁADÓW

EMPIRYCZNYCH

n

i

x

i

Rozkład jednomodalny

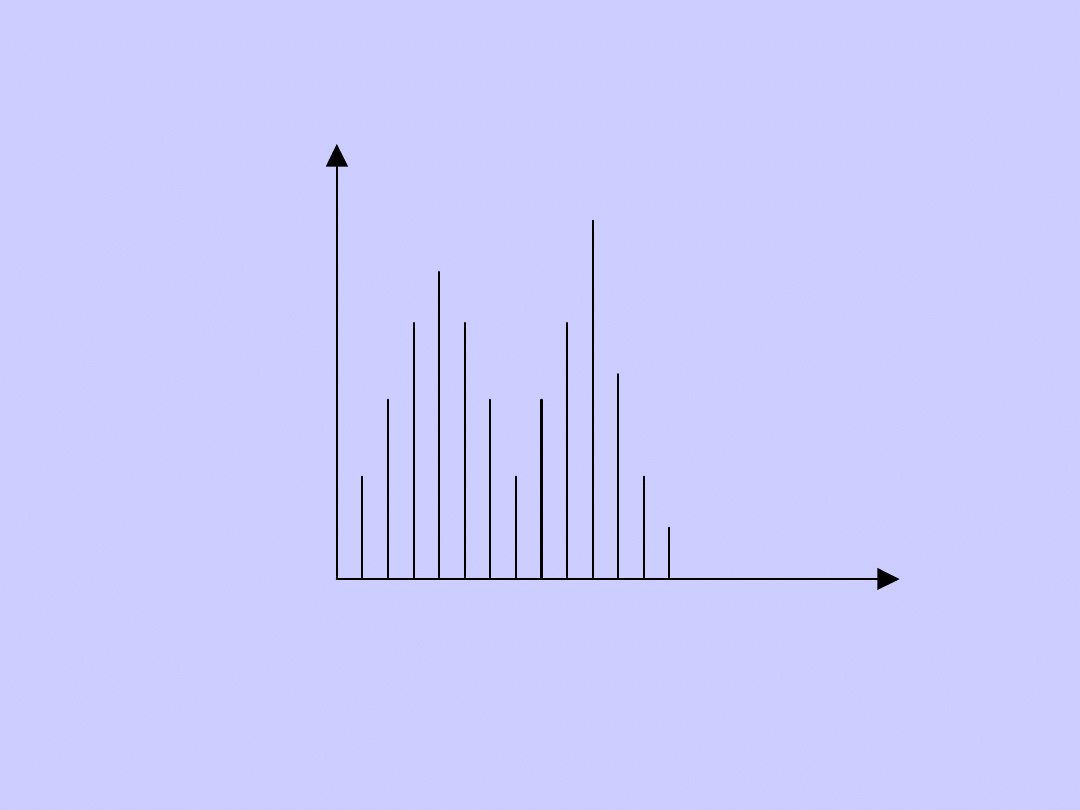
n

i

x

i

Rozkład bimodalny

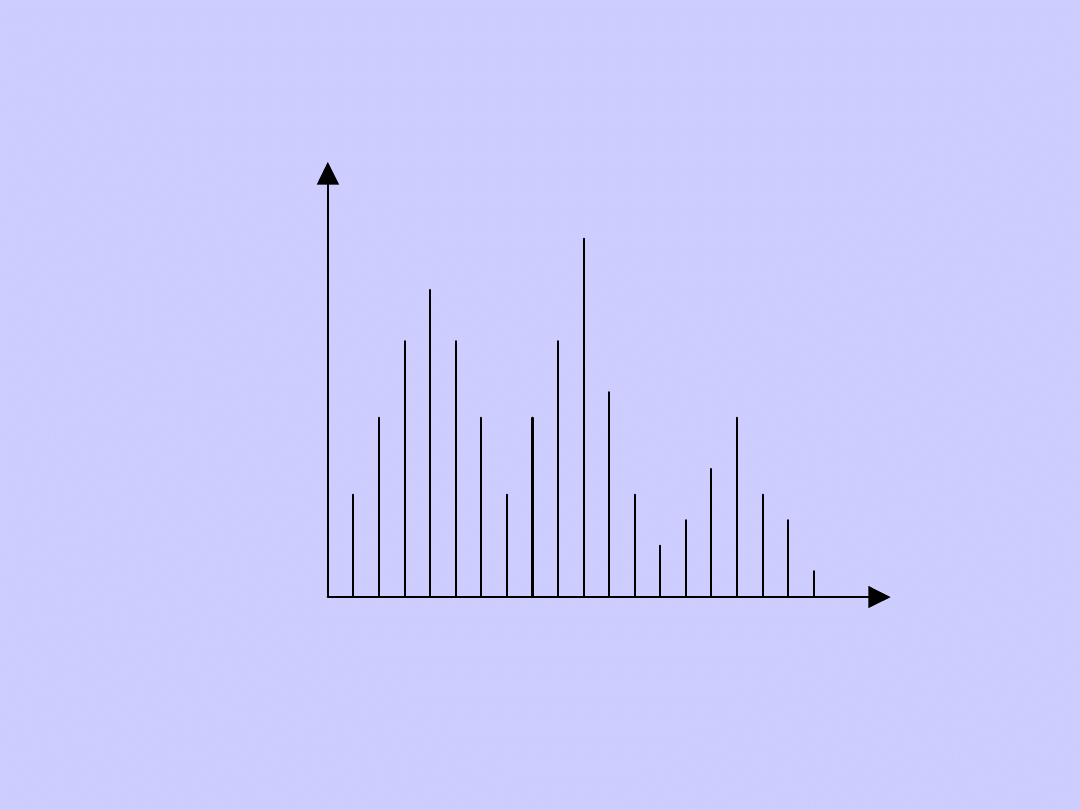
n

i

x

i

Rozkład wielomodalny

n

i

x

i

Rozkład skrajnie asymetryczny

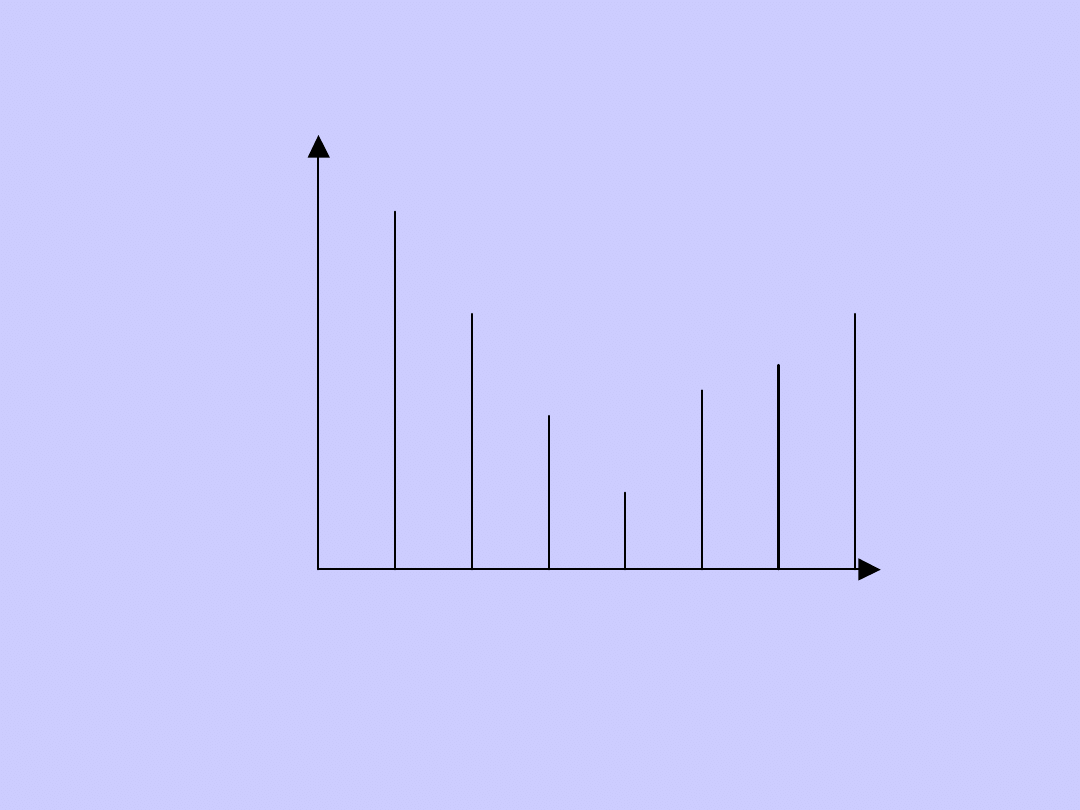
n

i

x

i

Rozkład siodłowy

n

i

x

i

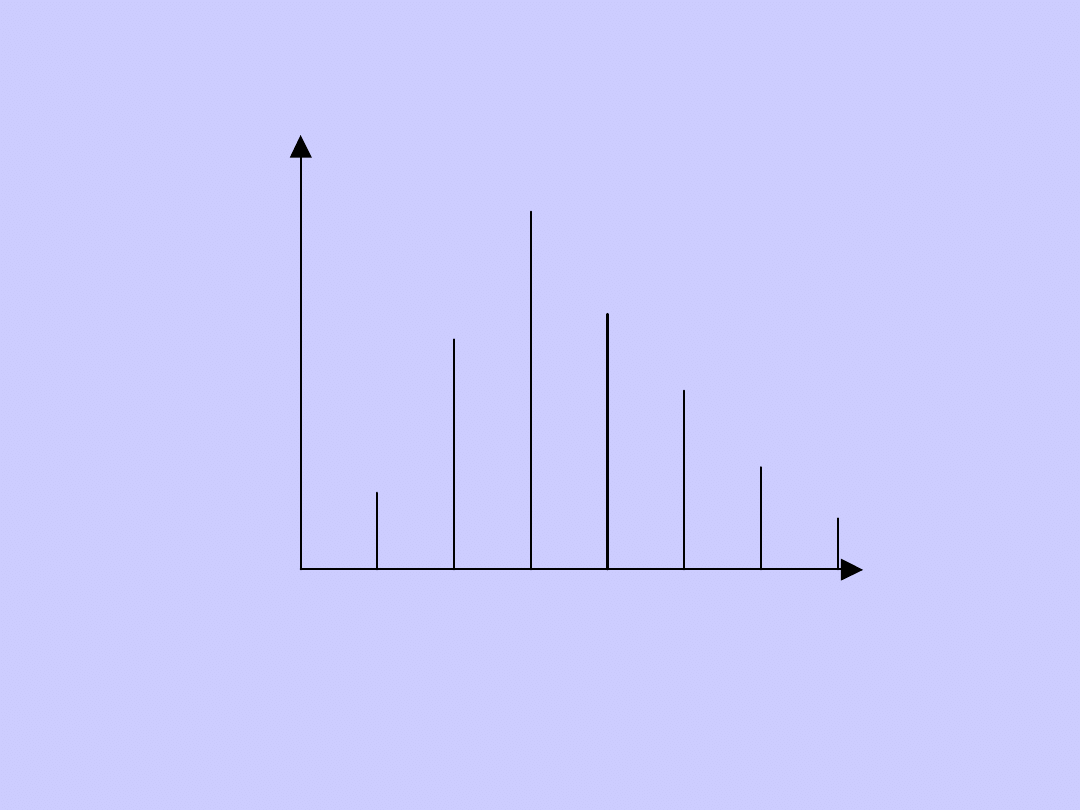
Rozkład umiarkowanie asymetryczny

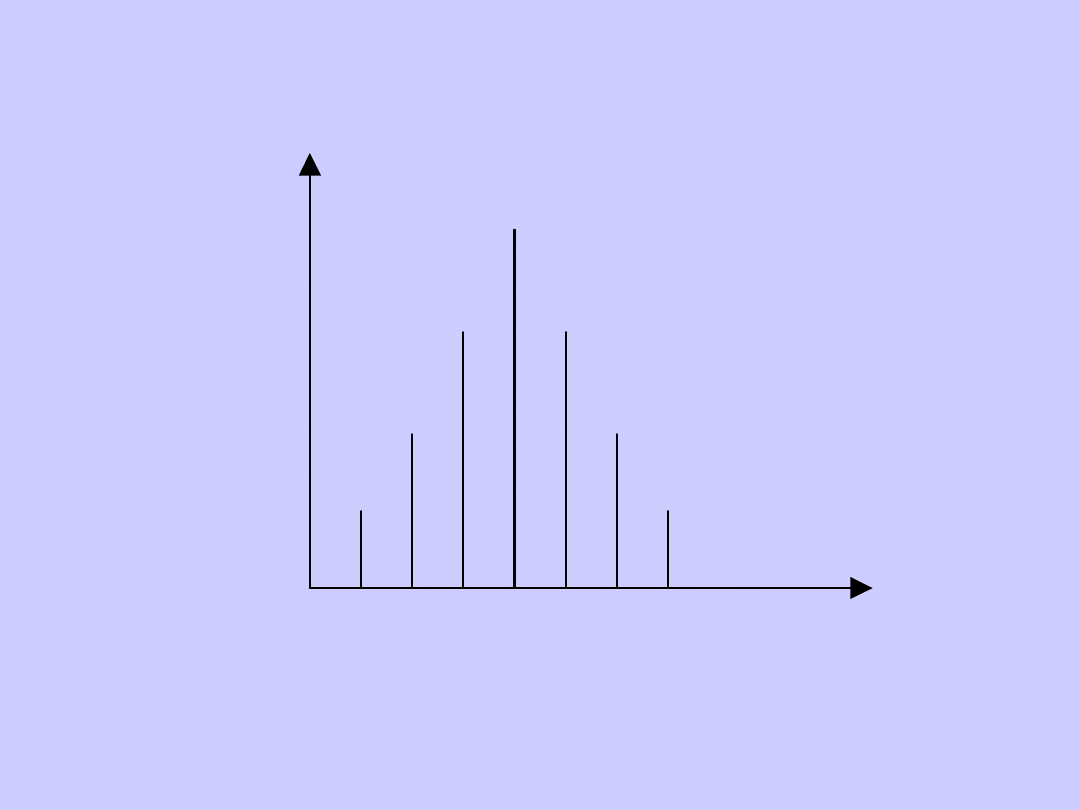
n

i

x

i

Rozkład symetryczny

n

i

x

i

Rozkład spłaszczony

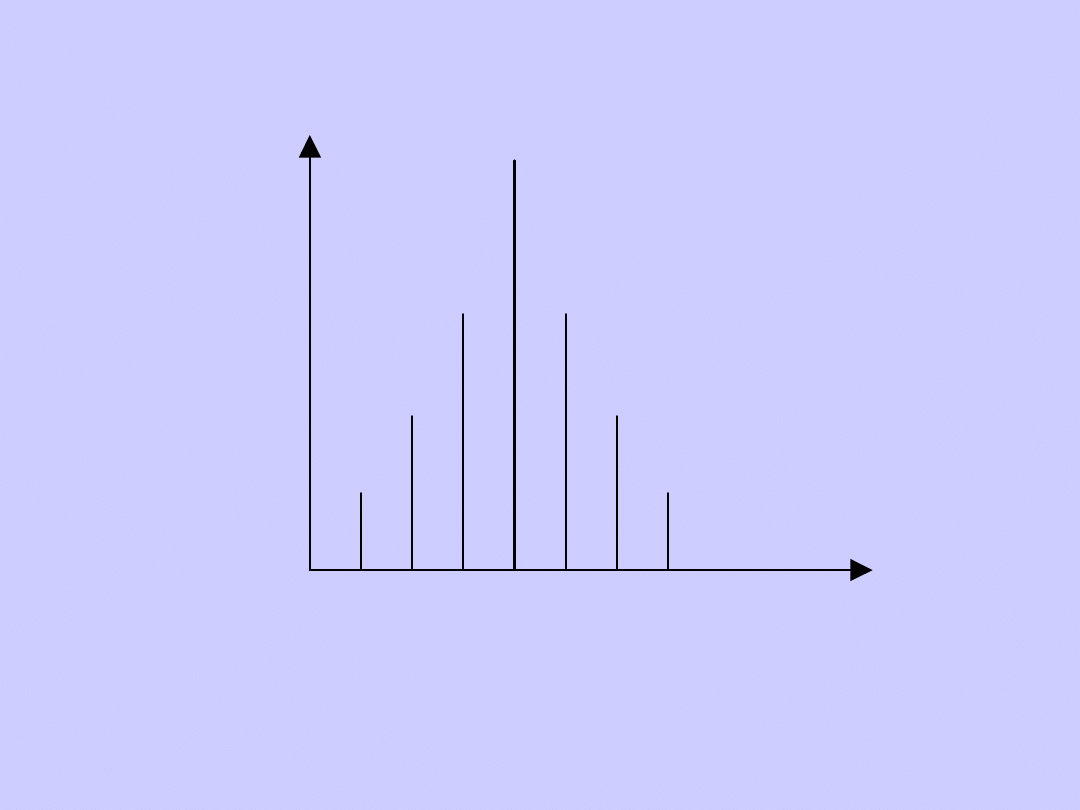
n

i

x

i

Rozkład wysmukły

OPISOWE CHARAKTERYSTYKI

ROZKŁADÓW

Przeprowadzając analizę struktury

zjawisk masowych należy zbadać:

1. tendencję centralną, czyli tzw. przeciętny

poziom

2. Zróżnicowanie wartości, czyli tzw.

dyspersję (zmienność, rozproszenie)

3. asymetrię rozkładu (skośność)
4. koncentrację.
Do przeprowadzenia tych badań

wykorzystuje się charakterystyki

nazywane parametrami. Charakterystyki

opisowe to liczby (wielkości), które

pozwalają w sposób syntetyczny określić

właściwości badanych rozkładów.

MIARY ŚREDNIE (PRZECIĘTNE)

Miary średnie pozwalają określić

tendencję centralną. Służą do

określania tej wartości zmiennej,

wokół której kupiają się wszystkie

pozostałe zmienne.

Podział średnich:
1. Średnie klasyczne.
2. Średnie pozycyjne.
Do średnich klasycznych zalicza się średnie:
1. arytmetyczną
2. geometryczną
3. harmoniczną.

Średnia arytmetyczna to suma

wartości zmiennej wszystkich
jednostek badanej zbiorowości
podzielona przez liczbę tych
jednostek:

gdzie:
x

i

– wartość cechy,

n – liczebność próby

















n

i

i

n

x

n

n

x

x

x

x

1

2

1

1

...

Jeżeli wartości zmiennej

występują z różną częstotliwością,
wówczas wylicza się średnią
arytmetyczną ważoną (wagami są
liczebności odpowiadające
poszczególnym wartościom):

gdzie:

























k

i

i

i

k

k

n

x

n

n

n

x

n

x

n

x

x

1

2

2

1

1

1

...







k

i

i

n

n

1

W przypadku danych zgrupowanych w

szereg rozdzielczy przedziałowy wzór
na średnią arytmetyczną jest
następujący:

gdzie:
- środek i-tego przedziału

klasowego.

Jeżeli zamiast liczebności

wykorzystywane są częstości w

i ,

wzór

na średnią arytmetyczną przyjmuje
postać:

























k

i

i

i

k

k

n

x

n

n

n

x

n

x

n

x

x

1

0

0

2

0

2

1

0

1

1

...

0

i

x









k

i

i

i

w

x

x

1

Szereg rozdzielczy

Nr klasy

Czas

reakcji na

lek

(w

minutach)

Liczebnoś

ć

(n

i

)

Wskaźnik

struktury

(%)

Liczebnoś

ć

kumulowa

na

1
2
3

4
5
6
7

8-12

13-17
18-22

23-27
28-32
33-37
38-42

4

29
38

80
35

9
5

2,0

14.9
19,0

40,0
17,5

4,5
2,5

4

33
71

151
186
195
200

Razem

200

100,0

Średnia arytmetyczna jest miarą prawidłową

jedynie w odniesieniu do zbiorowości
jednorodnych, o niewielkim zróżnicowaniu
wartości zmiennej. Średniej tej nie należy
stosować w przypadku rozkładów skrajnie
asymetrycznych, bimodalnych i
wielomodalnych. Nie oblicza się jej
również w przypadkach, gdy w
zbiorowości występują wartości skrajne.
Ponadto, średniej arytmetycznej nie należy
stosować dla szeregu o otwartych
przedziałach, jeżeli przedziały te
charakteryzują się dużą liczebnością.

Średnia harmoniczna jest

odwrotnością średniej arytmetycznej z
odwrotności wartości zmiennych. W
przypadku szeregów
szczegółowych (wyliczających) średnią
harmoniczną liczy się ze wzoru:







n

i

i

h

x

n

x

1

1

Dla szeregów rozdzielczych

punktowych średnią harmoniczną liczy
się z uwzględnieniem wag, tzn:







n

i

i

i

h

n

x

n

x

1

1

Dla szeregów rozdzielczych

przedziałowych średnią harmoniczną
liczy się następująco:

Średnią harmoniczną stosuje się

wówczas, gdy wartości zmiennej
podane są w jednostkach względnych.







n

i

i

i

h

n

x

n

x

1

0

1

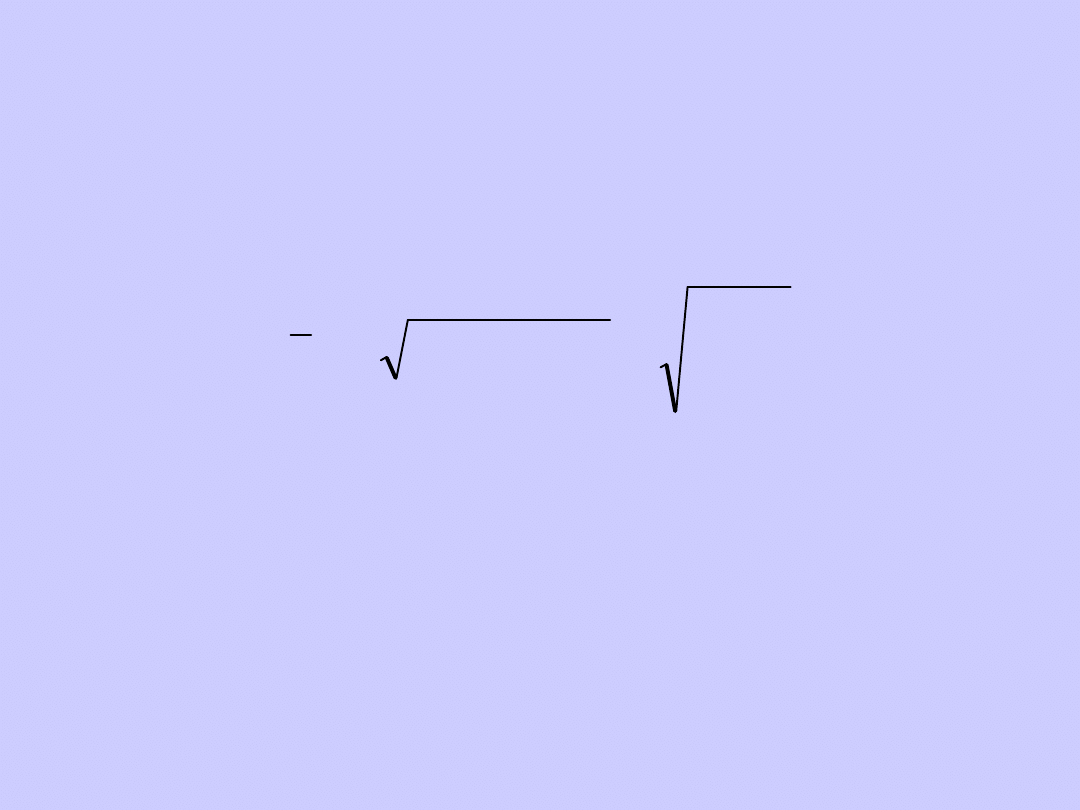
Średnia geometryczna jest

pierwiastkiem n-tego stopnia z
iloczynu n zmiennych:

gdzie:
- znak iloczynu.

n

n

i

i

n

n

g

x

x

x

x

x













1

2

1

...



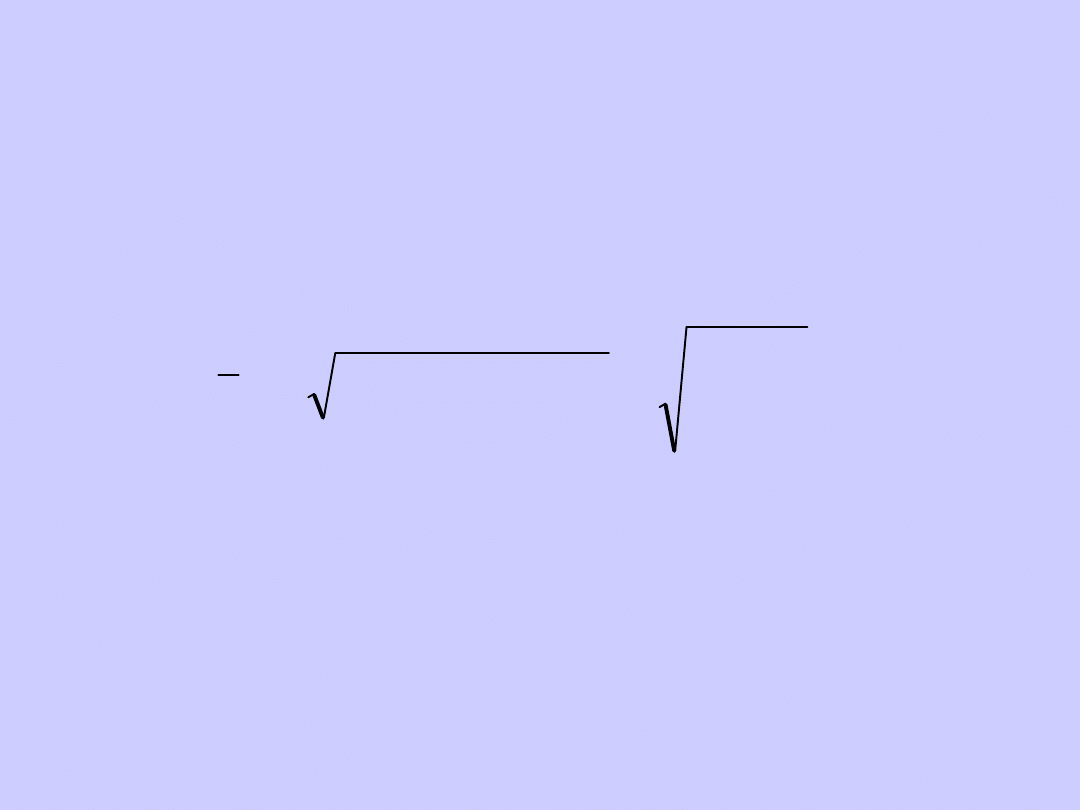
W przypadku, gdy wartości zmiennej

występują z różną częstotliwością,

średnią geometryczną wylicza się z

wykorzystaniem następującej formuły:

gdzie:

n

k

i

n

i

n

n

k

n

n

g

i

k

x

x

x

x

x















1

2

1

...

2

1

n

n

n

n

k









...

2

1

Średnią geometryczną stosuje się w

przypadkach, gdy wartości zmiennej tworzą postęp

geometryczny lub w przypadku rozkładu skrajnie

asymetrycznego.

Średnia ta ma zastosowanie przy badaniu

średniego tempa zmian.

Średniej geometrycznej nie należy stosować,

jeżeli którakolwiek z wartości zmiennej jest ujemna

lub równa zeru!!!

ŚREDNIE POZYCYJNE

Najczęściej wykorzystywanymi

średnimi pozycyjnymi są:
dominanta (moda, wartość
najczęstsza) oraz mediana
(wartość środkowa).

Dominantą nazywa się taką

wartość zmiennej, nie będącą ani
najmniejsza ani największą, która
w danym rozkładzie empirycznym
występuje najczęściej.

W szeregach rozdzielczych punktowych

jest tą wartością cechy, której odpowiada

największa liczebność.

W szeregach rozdzielczych przedziałowych

bezpośrednio można wyznaczyć wyłącznie

przedział zwany przedziałem dominanty

(jest to przedział o największej liczebności).

Wartość dominanty wyznacza się ze wzoru:

gdzie:
- dominanta
- dolna granica przedziału dominanty
- liczebność przedziału dominanty
- liczebność przedziału poprzedzającego przedział
dominanty
- liczebność przedziału następującego po przedziale
dominanty
- interwał (rozpiętość) przedziału dominanty.



 



D

D

D

D

D

D

D

D

i

n

n

n

n

n

n

x

D





















1

1

1

D

D

x

D

n

1



D

n

1



D

n

D

i

Dla szeregów rozdzielczych przedziałowych

dominantę można również wyznaczyć metodą graficzną,

która polega na wykreśleniu histogramu liczebności z

trzech przedziałów klasowych: przedziału dominanty oraz

dwóch przedziałów sąsiednich.

Wyznaczanie dominanty jest uzasadnione wówczas,

gdy szereg spełnia następujące warunki:

 rozkład empiryczny jest rozkładem jednomodalnym,
 asymetria rozkładu jest umiarkowana,
 przedział dominanty i przedziały sąsiednie mają jednakowe

rozpiętości.

Medianą określa się taką

wartość cechy, że co najmniej połowa
jednostek ma wartość cechy nie
większą niż i co
najmniej połowa ma wartość nie
mniejszą niż .

Medianą jest wartość cechy, którą

posiada środkowa jednostka w
uporządkowanym rosnąco ciągu
elementów zbiorowości.





Me

x

Me

i







Me

x

Me

i



Zatem:




















parzystego

n

dla

x

x

ego

nieparzyst

n

dla

x

Me

n

n

n

2

1

2

2

2

1

W przypadku szeregu

rozdzielczego przedziałowego medianę
wyznacza się metodą graficzną lub
rachunkową. W metodzie graficznej
wykorzystuje się wykres krzywej
liczebności skumulowanej.

Jeżeli dane są przedstawione za

pomocą szeregu rozdzielczego
punktowego (cecha skokowa) –
medianą jest pierwsza wartość,
której odpowiada co najmniej
połowa skumulowanej liczebności.

Jeżeli mamy do czynienia z szeregiem rozdzielczym

klasowym (dla cechy ciągłej) medianę można wyznaczyć

wykorzystując wzór:

gdzie:
- liczebność i-tej klasy
- liczebność zbiorowości (próby)
- numer klasy zawierającej medianę
- dolna granica przedziału, w którym znajduje się
mediana
- interwał (rozpiętość) przedziału mediany
- liczebność przedziału mediany.



























1

1

2

m

i

i

m

m

om

n

n

n

i

x

Me

i

n

n
m

om

x

m

i

m

n

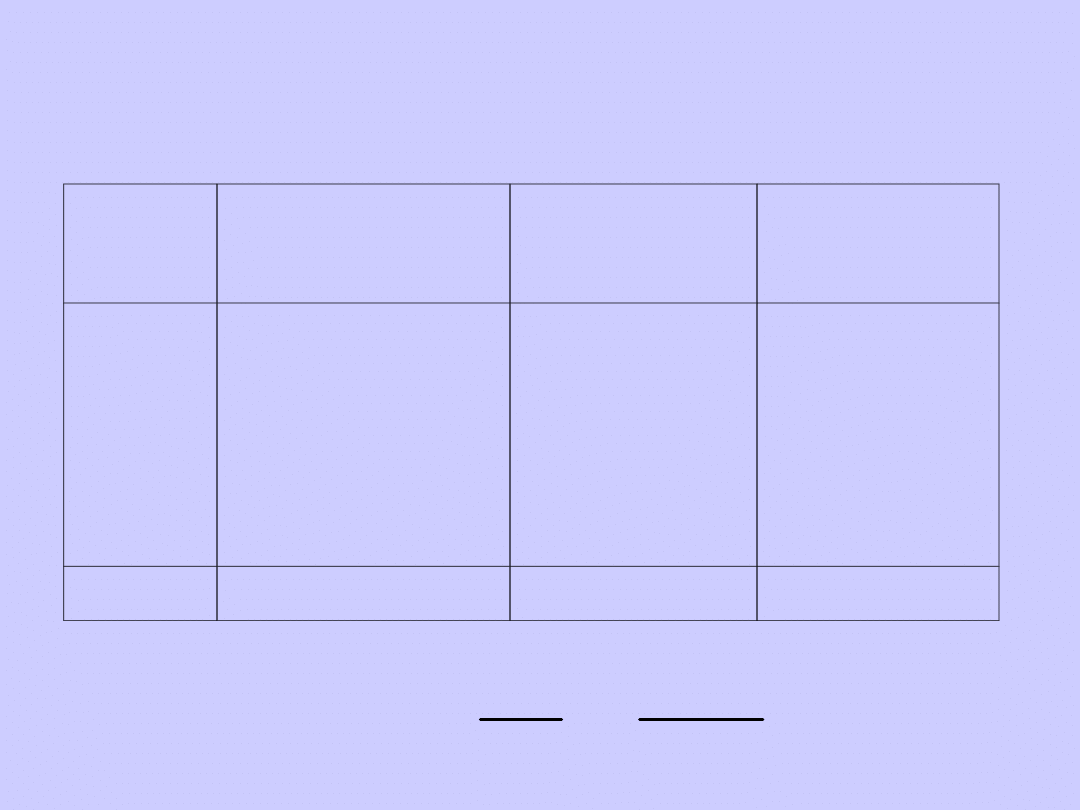
Medianą wyliczoną na podstawie powyższego

wzoru dla czasu reakcji na lek w oparciu o

poniższe dane wynosi:

Nr klasy

Czas reakcji na

lek

(w minutach)

Liczebność

(n

i

)

Liczebność

kumulowana

1
2
3
4

5
6
7

8-12

13-17
18-22
23-27

28-32
33-37
38-42

4

29
38
80

35

9
5

4

33
71

151

186
195
200

Razem

200





















71

2

200

80

5

23

Me





















71

2

200

80

5

23

Me

MIARY ZMIENNOŚCI

Na zjawiska masowe oddziałują

dwa rodzaje przyczyn:

1.

Główne (wywołujące zmienność
systematyczną)

2.

Uboczne (wywołujące zmienność
przypadkową)

Przybliżonym miernikiem

składnika systematycznego zbiorowości
są miary przeciętne (średnie).
Odchylenia wartości poszczególnych
jednostek zbiorowości od wartości
średniej powstają pod wpływem
przyczyn przypadkowych (ubocznych).

Do pomiaru tych odchyleń

wykorzystuje się miary zmienności

(zróżnicowania, dyspersji,

rozproszenia).

Dyspersja to zróżnicowanie jednostek

badanej zbiorowości ze względu na

wartość badanej cechy statystycznej. Siłę

dyspersji można oceniać

za pomocą miar:

1. Klasycznych
2. Pozycyjnych.
Punktem odniesienia w miarach

klasycznych jest średnia arytmetyczna,

zaś miary pozycyjne wyznaczane są

przede wszystkim na podstawie kwartyli.

Miary klasyczne:
1. Wariancja
2. Odchylenie standardowe
3. Odchylenie przeciętne (dewiata)
4. Współczynnik zmienności*.

* - jeśli do jego wyliczenia

wykorzystywana jest średnia
arytmetyczna oraz odchylenie
standardowe)

Miary pozycyjne:
1. Empiryczny obszar zmienności

(rozstęp, amplituda wahań, pole
rozsiania)

2. Odchylenie ćwiartkowe
3. Współczynnik zmienności**.

** - jeśli do jego wyliczenia

wykorzystywana jest mediana oraz
odchylenie ćwiartkowe)

Najczęściej stosowane miary

rozproszenia:

1. Obszar zmienności
2. Odchylenie przeciętne
3. Wariancja
4. Odchylenie standardowe
5. Współczynnik zmienności.

Obszarem zmienności określa się

różnicę pomiędzy największą a najmniejszą

wartością zmiennej, tzn.:

Miara ta ma niewielką wartość

poznawczą, gdyż obszar zmienności

uzależniony jest

od wartości skrajnych, które często różnią

się istotnie od wszystkich pozostałych

wartości zmiennej. Na obszar zmienności

wpływają tylko wartości skrajne,

pozostałe zaś nie mają żadnego

wpływu na wynik. Obszar zmienności

wykorzystywany jest jedynie przy

wstępnej ocenie rozproszenia.

min

max

x

x

R





Odchyleniem przeciętnym d nazywa

się średnią arytmetyczną z

bezwzględnych odchyleń wartości zmiennej

x od średniej arytmetycznej.

Odchylenie przeciętne wyznaczamy z

następujących wzorów:

- dla szeregu szczegółowego:

gdzie:
n - liczebność badanej zbiorowości
- wartości przyjmowane przez cechę mierzalną
- średnia arytmetyczna badanej zbiorowości











n

i

i

x

x

n

d

1

1

i

x
x

-

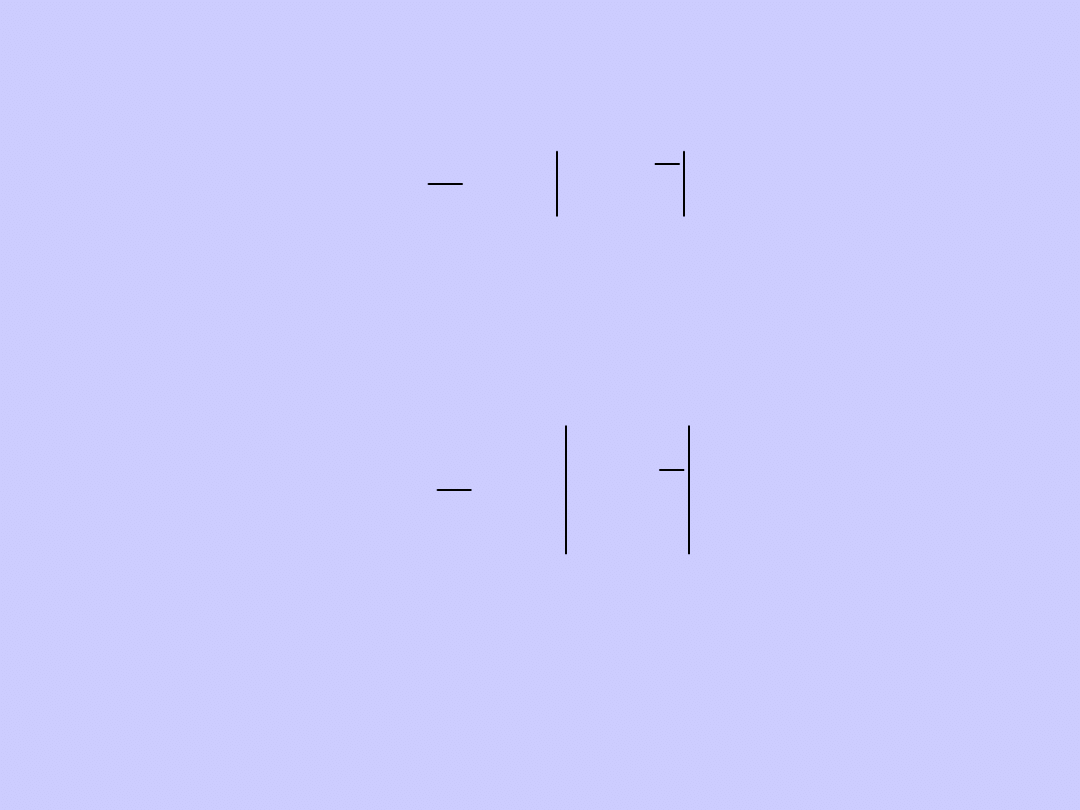
dla szeregu rozdzielczego punktowego:

-

dla szeregu rozdzielczego
przedziałowego:

gdzie:
- środek i-tego przedziału klasowego

i

k

i

i

n

x

x

n

d











1

1

i

k

i

i

n

x

x

n

d











1

0

1

i

x

0

Wariancją określa się średnią

arytmetyczną z sumy kwadratów
odchyleń poszczególnych wartości
cechy statystycznej od średniej
arytmetycznej całej zbiorowości
statystycznej. Wariancję wyznacza
się z następujących wzorów:

- dla szeregu szczegółowego:















n

i

i

x

x

n

s

1

2

2

1

2

s

- dla szeregu rozdzielczego

punktowego:

- dla szeregu rozdzielczego

przedziałowego:





i

n

i

i

n

x

x

n

s











1

2

2

1

i

n

i

i

n

x

x

n

s













 







1

2

0

2

1

Podstawowe właściwości wariancji:
1. Jest zawsze liczbą nieujemną
2. Jest zawsze wielkością

mianowaną, tzn. wyrażoną w
jednostkach badanej cechy
statystycznej. Miano wariancji
zawsze jest kwadratem jednostki
fizycznej, w jakiej mierzona jest
badana cecha

3. Im zbiorowość statystyczna jest

bardziej zróżnicowana, tym wartość
wariancji jest wyższa

4.

Wariancja, jako miara dyspersji

wykorzystywana dla szeregów
rozdzielczych przedziałowych, daje
zawsze wartości zawyżone. Przyczyna
zawyżenia wartości wynika z
faktu, iż w przypadku szeregów
rozdzielczych przedziałowych korzysta
się ze środków przedziałów. W
celu zmniejszenia popełnionego błędu,
przy obliczaniu wariancji w przypadku
przedziałów o zbyt dużej rozpiętości (i),
stosuje się tzw. poprawkę Shepparda.
Wzór na wariancję przyjmuje wówczas
postać:

2

2

2

12

1

i

s

s

pop







Odchylenie standardowe jest

pierwiastkiem kwadratowym z
wariancji:

gdzie:
- odchylenie standardowe
- wariancja.
Odchylenie standardowe określa,

o ile wszystkie jednostki
statystyczne danej zbiorowości różnią
się średnio od wartości średniej
arytmetycznej badanej zmiennej.

2

s

s 

s

2

s

W statystyce odchylenie

standardowe wykorzystywane jest do

tworzenia typowego obszaru zmienności

statystycznej. W obszarze takim mieści

się około 2/3 wszystkich jednostek

badanej zbiorowości statystycznej.

Typowy obszar zmienności określa wzór:

Użyteczność kategorii typowego

obszaru zmienności sprowadza się przede

wszystkim do rozdziału jednostek

statystycznych

na typowe (tzn. występujące

stosunkowo często) i nietypowe (tzn.

występujące stosunkowo rzadko).

s

x

x

s

x

typ









Z odchyleniem standardowym

łączy się pojęcie zmiennej
standaryzowanej (unormowanej)
dla rozkładu empirycznego cechy
mierzalnej :

is

x

s

x

x

x

i

is





Miary dyspersji (rozproszenia),

jak i wartości średnie są liczbami
mianowanymi. Fakt ten
umożliwia bezpośrednie
porównywania miar dyspersji
obliczonych dla różnych szeregów.

Jeżeli badane zjawisko mierzone

jest w różnych jednostkach miary lub
kształtuje się na niejednakowym
poziomie, wówczas do oceny
rozproszenia należy stosować
współczynnik zmienności.

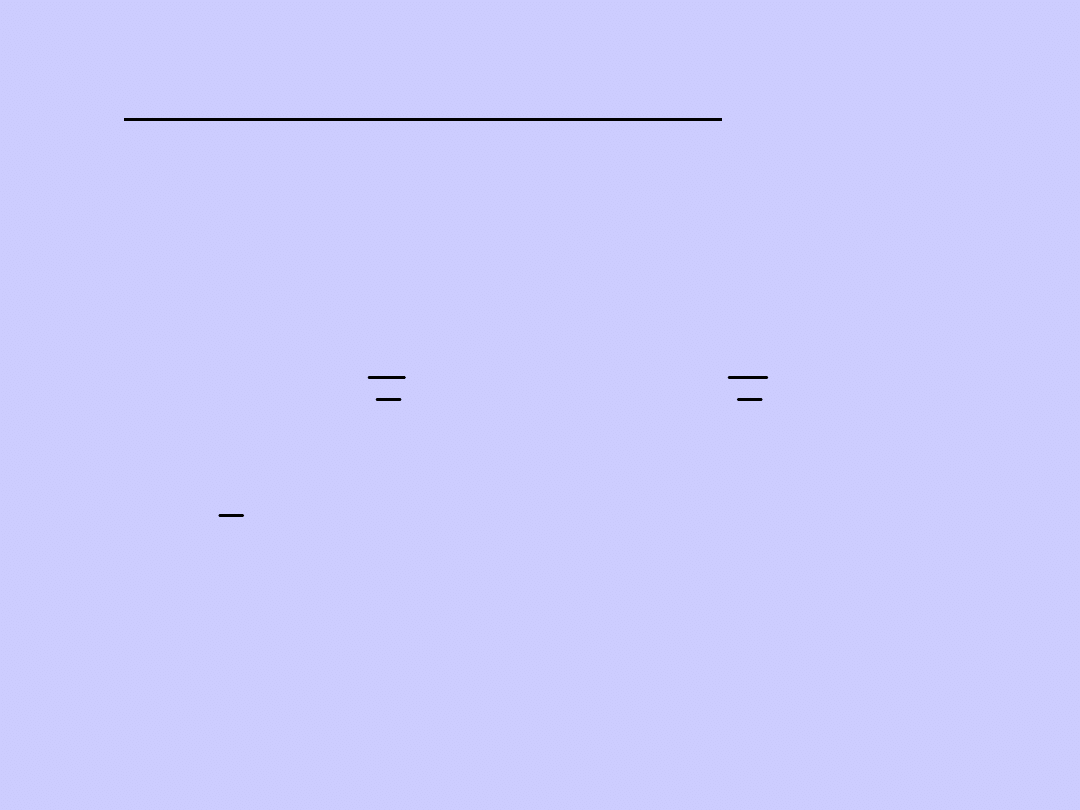
Współczynnik zmienności jest ilorazem

odchylenia przeciętnego lub odchylenia
standardowego oraz średniej:

lub

(zamiast może być inna średnia, np.

mediana)

Współczynnik zmienności może

być wyrażony w procentach.
Współczynnik ten zastępuje
bezwzględne miary dyspersji.

x

s

V 

x

d

V 

x

Współczynnik zmienności

pozwala porównywać różne
szeregi lub szeregi tego
samego typu, ale o różnej
strukturze. Umożliwia on
dokonanie analiz zmienności w
czasie i przestrzeni.
Współczynnik zmienności (obok
odchylenia standardowego)
wykorzystywany jest jako miara
ryzyka finansowego.

MIARY ASYMETRII (SKOŚNOŚCI)

Szczegółowa analiza statystyczna

powinna zawierać nie tylko

poziom przeciętny i wewnętrzne

zróżnicowanie zbiorowości. Istotne

jest również określenie, czy

przeważająca liczba jednostek

znajduje się powyżej czy poniżej

przeciętnego poziomu badanej cechy.

Należy dokonać zatem oceny

asymetrii rozkładu. W związku z

tym określa się charakter (kierunek)

oraz natężenie (rozmiar) skośności.

W zjawiskach społeczno-

gospodarczych zwykle spotyka się
skośność dodatnią (prawostronną).

Skośność ta często występuje w

badaniach:

- dochodów,

- wykonania norm pracy, planów pracy,
- absencji w pracy,
- wkładów oszczędnościowych,
- odległości przewozów osób, czy

towarów.

Skośność dodatnia

(prawostronna) ma miejsce
wówczas, gdy dłuższe ramię krzywej
charakteryzującej rozkład
liczebności szeregu znajduje się
po prawej stronie średniej.

Jeżeli dłuższe ramię krzywej

znajduje się po lewej stronie
średniej, wówczas można mówić o
skośności ujemnej (lewostronnej).

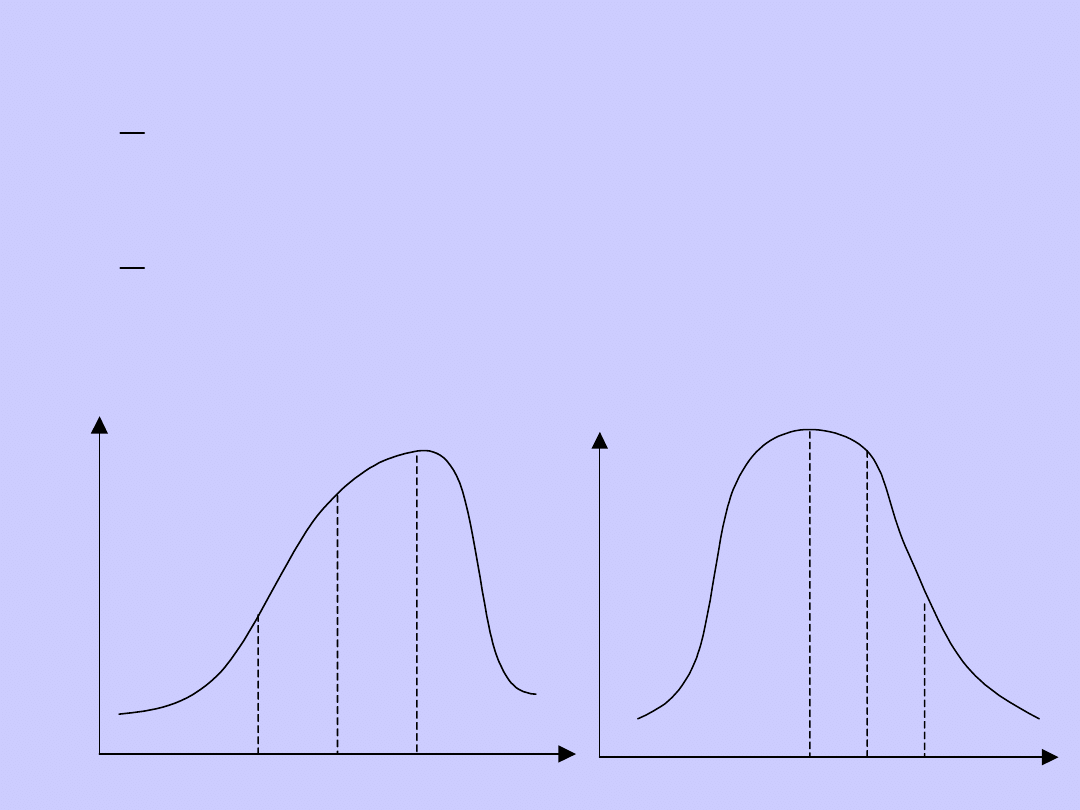
Inaczej: jeśli spełniona jest

nierówność:

to rozkład

charakteryzuje się asymetrią
prawostronną. Jeżeli natomiast:

to można

wówczas mówić o asymetrii
lewostronnej.

D

Me

x





D

Me

x





n

i

x Me D x

i

n

i

D Me x x

i

Charakter asymetrii można

również określać na podstawie
punktów wyznaczonych przez
dominantę, medianę i średnią
arytmetyczną.

W szeregu symetrycznym wszystkie

miary pozycyjne są sobie równe.

W szeregu asymetrycznym

miary te kształtują się na
różnym poziomie: im większa
skośność, tym większe są różnice
pomiędzy dominantą, medianą i
średnią arytmetyczną.

Jednym z mierników skośności jest

wskaźnik skośności (inaczej:
bezwzględna miara skośności):

Wskaźnik ten jest bezwzględną

miarą asymetrii posiadającą miano
badanej cechy. Z tego względu
ma on ograniczone zastosowanie
w analizie porównawczej. Poza tym,
wskaźnik skośności określa jedynie
kierunek asymetrii (prawo-, czy
lewostronna) nie wskazując jej siły.

D

x

Ws





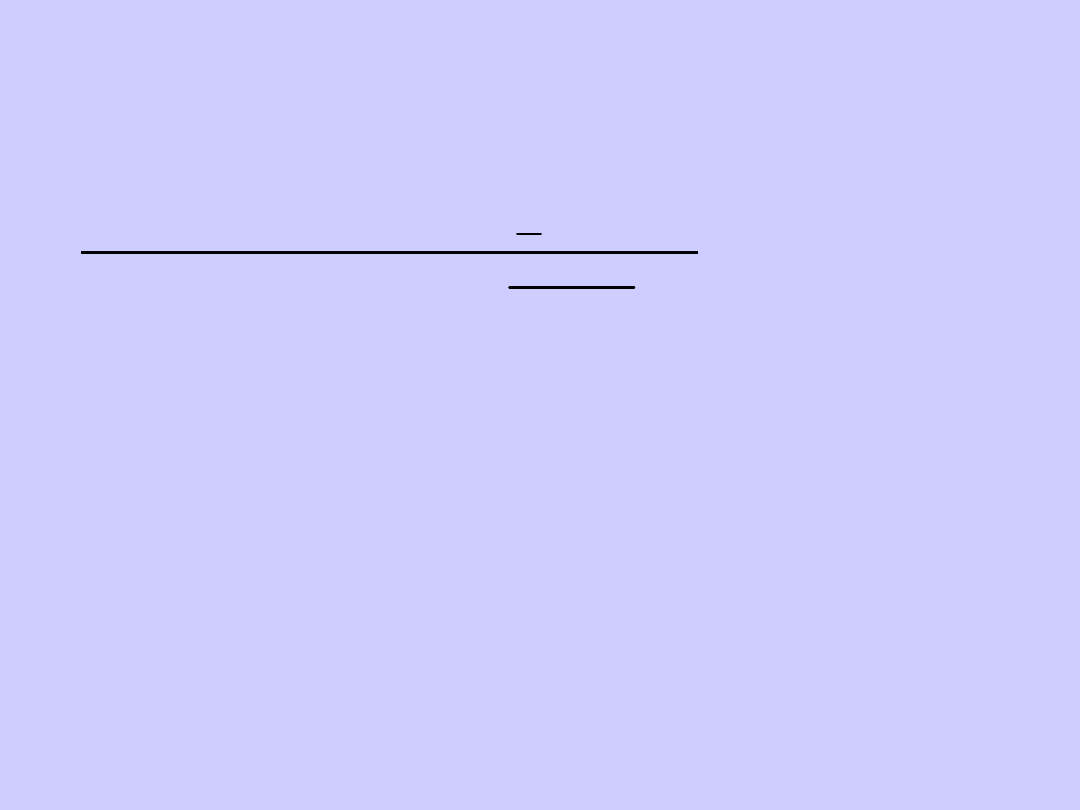
Miarą określającą zarówno

kierunek jak i siłę asymetrii jest
współczynnik skośności:

Współczynnik ten przyjmuje

zazwyczaj wartości z przedziału:
<-1;1>. Jedynie przy bardzo silnej
asymetrii wartość współczynnika
może wykroczyć poza w/w
przedział.

s

D

x

As





Jeżeli dany rozkład jest symetryczny,

wówczas .

W przypadku asymetrii

prawostronnej:

.
Dla rozkładu o asymetrii

lewostronnej:

.
Im silniejsza jest asymetria

rozkładu, tym wartość bezwzględna
współczynnika skośności jest wyższa.

0



As

0



As

0



As

ANALIZA WSPÓŁZALEŻNOŚCI

Analiza struktury zjawisk dotyczyła

jednej cechy. W praktyce jednak bywa
tak, że badane jednostki statystyczne
charakteryzowane są przez kilka cech.
Cechy te nie są od siebie odizolowane,
mają na siebie wpływ oraz
posiadają wzajemne uwarunkowania.
Dlatego często zachodzi
potrzeba badania współzależności
między tymi cechami.

Przeprowadzając analizę można spotkać

dwa rodzaje współzależności zmiennych:

1. Współzależność funkcyjną, polegającą na

tym, że zmiana wartości jednej zmiennej
pociąga określoną zmianę wartości drugiej
zmiennej.

2. Współzależność stochastyczną

(probabilistyczną), polegającą na tym, że
wraz ze zmianą jednej zmiennej zmienia
się rozkład prawdopodobieństwa drugiej
zmiennej. Szczególnym przypadkiem
zależności stochastycznej jest
zależność korelacyjna.

Zależności korelacyjne zachodzą

wówczas, gdy określonym
wartościom jednej zmiennej
odpowiadają ściśle określone
średnie wartości drugiej zmiennej.

Zdarzają się jednak sytuacje, w

których nie istnieje
współzależność (korelacja) ale ma
miejsce zbieżność występowania
zjawisk. Taką zbieżność określa się
mianem korelacji pozornej.

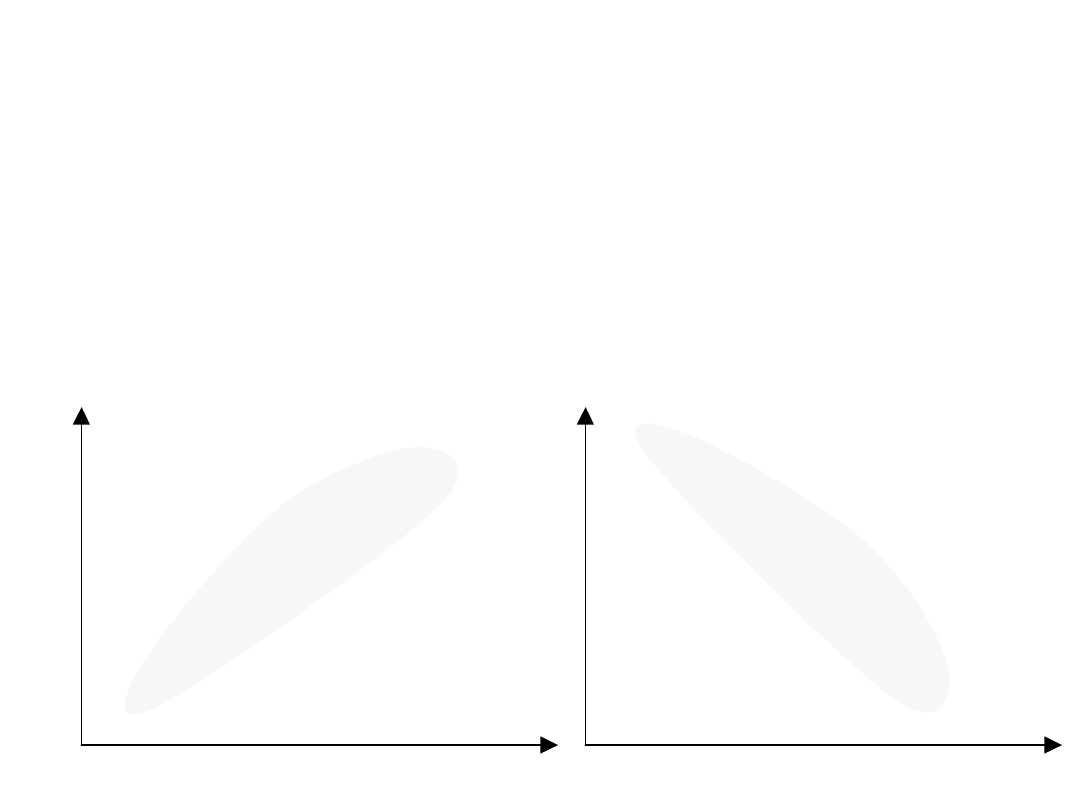
Najczęściej spotykanymi

metodami wykrywania związków
korelacyjnych są:

1. Metoda porównywania

przebiegu szeregów
statystycznych.

2. Metoda graficzna.

y

i

0 x

i

y

i

0 x

i

•

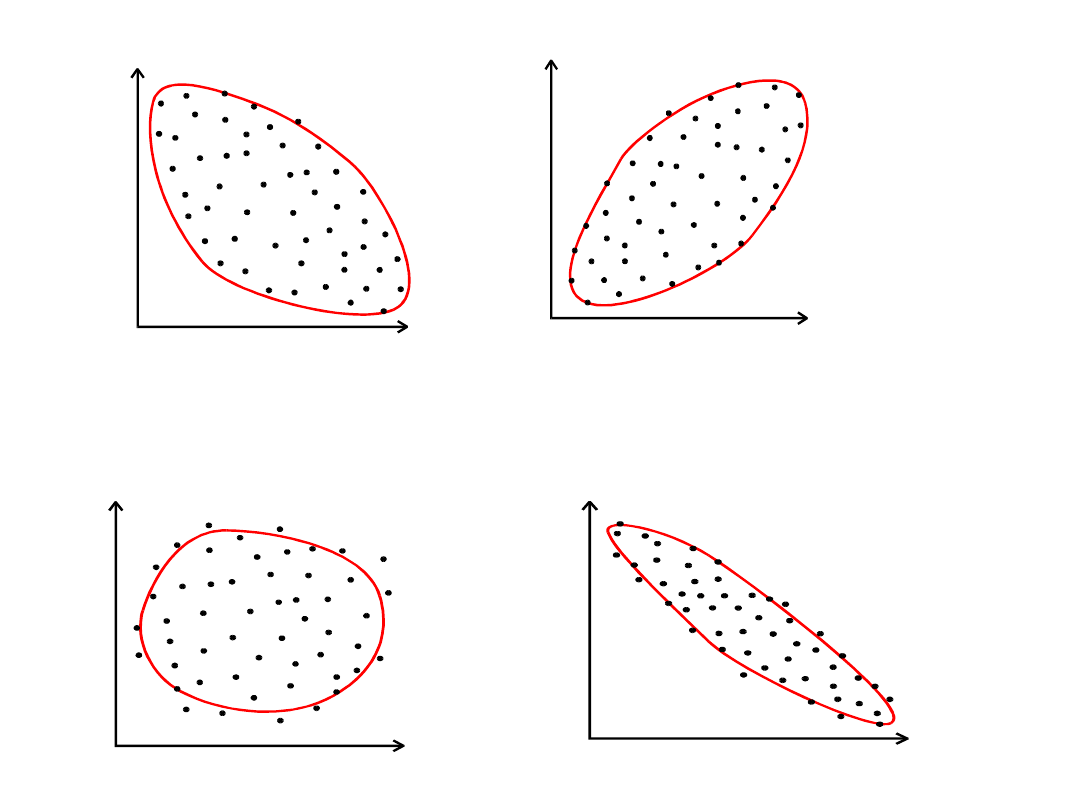
X

Y

Brak związku

X

Y

Związek silny

X

Y

X

Y

Związek dodatni

(wzrost

wartościchy X

indukuje wzrost

wartości cechy Y

Cechę dwuwymiarową oznacza

się jako uporządkowaną parę
(X,Y). Składowymi mogą być
zarówno cechy ilościowe jak i
jakościowe. To od tego, z jakimi
cechami mamy do czynienia zależy
wybór sposobu opisu współzależności.

Podstawą analizy jest zbiorowość

jednostek scharakteryzowanych
parą własności, gdzie i=1,2,...,n.

Badając zbiorowość jednostek pod

względem

wyróżnionych cech otrzymuje

się ciąg par wartości:



 

 



.

,

,...,

,

,

,

2

2

1

1

n

n

y

x

y

x

y

x





i

i

y

x ,

MIARY WSPÓŁZALEŻNOŚCI

Do badania zależności między

zmiennymi X i Y wykorzystuje się
najczęściej współczynnik korelacji
liniowej Pearsona, będący miarą siły
związku prostoliniowego między
dwiema cechami mierzalnymi.
Współczynnik ten wylicza się ze wzoru:

gdzie:
cov(x,y) - kowariancja zmiennych X i Y
s - odchylenie standardowe.

 

   

y

s

x

s

y

x

r

xy





,

cov

Kowariancja jest średnią arytmetyczną

iloczynu odchyleń zmiennych X i Y od
ich średnich arytmetycznych:

Rozpatrując kowariancję uzyskać

można następujące informacje o
istniejącym związku pomiędzy
zmiennymi X i Y:

1.

Jeżeli cov(x,y)>0 – dodatnia korelacja

2.

Jeżeli cov(x,y)<0 – ujmena korelacja

3.

Jeżeli cov(x,y)=0 – brak korelacji

 



 

















n

i

i

i

y

y

x

x

n

y

x

1

1

,

cov

Kowariancji nie można

stosować do bezpośrednich
porównań. Dlatego jest ona
standaryzowana przez odchylenia
standardowe, dzięki czemu otrzymuje
się współczynnik korelacji liniowej
Pearsona.

Właściwości współczynnika korelacji:
1. Przyjmuje wartości z przedziału <-1;1>
2. Dodatni znak świadczy o dodatnim, zaś

ujemny o ujemnym związku korelacyjnym

3. Im tym związek

korelacyjny jest silniejszy.

0



xy

r

Sposoby komentowania współczynnika korelacji:
a) - współzależność nie występuje,
b) - słaby stopień współzależności,
c) - umiarkowany (średni) stopień

współzależności,
d) - znaczny stopień współzależności,
e) - wysoki stopień współzależności,
f) - bardzo wysoki stopień
współzależności,
g) - całkowita (ścisła) współzależność
(zależność funkcyjna

pomiędzy

badanymi cechami).

0



XY

r

3

,

0

0





XY

r

5

,

0

3

,

0





XY

r

7

,

0

5

,

0





XY

r

9

,

0

7

,

0





XY

r

1

9

,

0





XY

r

1



XY

r

Analizę współzależności należy

uzupełnić o współczynnik
determinacji, będący kwadratem
współczynnika korelacji liniowej
Pearsona ( ).

Współczynnik determinacji informuje,

jaka część zmiennej objaśnianej jest
wyjaśniona przez zmienną objaśniającą.
Przy pomocy tego współczynnika można
wnioskować, czy na zmienną
objaśniającą wpływają również inne
czynniki, nie podlegające badaniu.

2

xy

r

W sytuacji, gdy obserwacje

statystyczne dotyczące badanych
zmiennych są liczne, bazowanie na
wartościach szczegółowych może być
uciążliwe. W celu zapewnienia
przejrzystości zebranych danych sporządza
się wówczas tablicę korelacyjną.

Na skrzyżowaniu kolumn z

wierszami wpisuje się liczebności
jednostek zbiorowości statystycznej, u
których zaobserwowano jednoczesne
występowanie określonych wartości
i .

i

x

i

y

Schemat tablicy korelacyjnej:

x

i

y

j

y

1

y

2

...

y

t

i

t

i

ij

n

n 



1

x

1

x

2

.
.
.

x

k

n

11

n

21

.
.
.

n

k1

n

12

n

22

.
.
.

n

k2

.
.
.
.
.
.

n

1t

n

2t

.
.
.

n

kt

n

1

n

2

.
.
.

n

k

j

k

i

ij

n

n 



1

n

.1

n

.2

…

n

.t

n

W tablicy korelacyjnej zawarte są

rozkłady brzegowe i warunkowe.

Rozkład brzegowy (por. ostatnia

kolumna określa rozkład brzegowy

cechy X, ostatni wiersz – rozkład

brzegowy cechy Y) prezentuje

strukturę wartości jednej zmiennej (X

lub Y) bez względu na kształtowanie

się wartości drugiej zmiennej.

Rozkłady brzegowe i warunkowe

mogą być scharakteryzowane pewnymi

sumarycznymi wielkościami (najczęściej

są to średnie arytmetyczne)

Średnie arytmetyczne z

rozkładów brzegowych wyznacza
się ze wzorów:

Średnie arytmetyczne z

rozkładów warunkowych oblicza
się następująco:

i

k

i

i

n

x

n

x









1

1

j

t

i

j

n

y

n

y









1

1

ij

k

i

i

j

j

n

x

n

x









1

.

1

ij

t

i

j

i

i

n

y

n

y









1

.

1

W sytuacji, gdy wraz ze

wzrostem (spadkiem) wartości
jednej zmiennej następuje wzrost
(spadek) warunkowych średnich
drugiej zmiennej, wówczas można
stwierdzić istnienie korelacji
dodatniej między zmiennymi. W
sytuacji, kiedy występuje
przeciwny kierunek zmian,
można mówić o korelacji ujemnej.

Jeżeli różnice pomiędzy średnimi

są takie same, tzn.:

wówczas związek między

zmiennymi jest liniowy.

1

2

3

1

2

...















t

t

x

x

x

x

x

x

1

2

3

1

2

...















k

k

y

y

y

y

y

y

Innym miernikiem korelacyjnego związku

cech jest współczynnik korelacji rang
Spearmana. Współczynnik ten stosowany
jest głównie do badania
współzależności cech niemierzalnych, bądź
cechy mierzalnej i niemierzalnej. Może być
on również stosowany w badaniu
związku korelacyjnego pomiędzy cechami
mierzalnymi (szczególnie w przypadku małej
próby).

Konstrukcja współczynnika korelacji

rang opiera się na zgodności pozycji, którą
zajmuje każda z odpowiadających sobie
wielkości we wzrastającym lub
malejącym szeregu wartości cechy.

Współczynnik korelacji rang

Spearmana (Q) wylicza się w
oparciu o wyznaczone różnice rang
( ) oraz liczby par obserwacji (n):

przy czym:

gdzie:
- rangi zmiennej X oraz Y

(i=1,2,...n)

i

d

n

n

d

Q

n

i

i













3

1

2

6

1

i

i

y

x

i

v

v

d





i

i

y

x

v

v ,

gdy

Współczynnik korelacji rang

przyjmuje wartości z przedziału
, a jego interpretacja
jest analogiczna do
współczynnika korelacji
Pearsona.

1



Q

0

1

2







n

i

i

d

1

1







Q