1

Podstawowe pojęcia statystyki
matematycznej.
Statystyka opisowa.

Zakład Doświadczalnictwa
Prof. dr hab. inż. Andrzej
Gregorczyk
ul. Pawła VI 3, pok. 112

2

Zalecana literatura

1. Koronacki J., Mielniczuk J. – Statystyka dla

studentów kierunków technicznych i

przyrodniczych.

WNT, Warszawa.
2. Klonecki W. – Statystyka dla inżynierów. PWN,

Warszawa.

3. Markiewska-Krawiec D., Krawiec B. - Podstawy

statystyki matematycznej. Wyd. AR Szczecin.

4. Bruchwald A. – Statystyka matematyczna dla

leśników. Wyd. SGGW.

3

Wprowadzenie

Geneza statystyki matematycznej
jako dziedziny naukowej

Definicja statystyki – jest to nauka
zajmująca się badaniem
prawidłowości w masowych
zjawiskach przypadkowych i
opisywaniem ich za pomocą liczb.

4

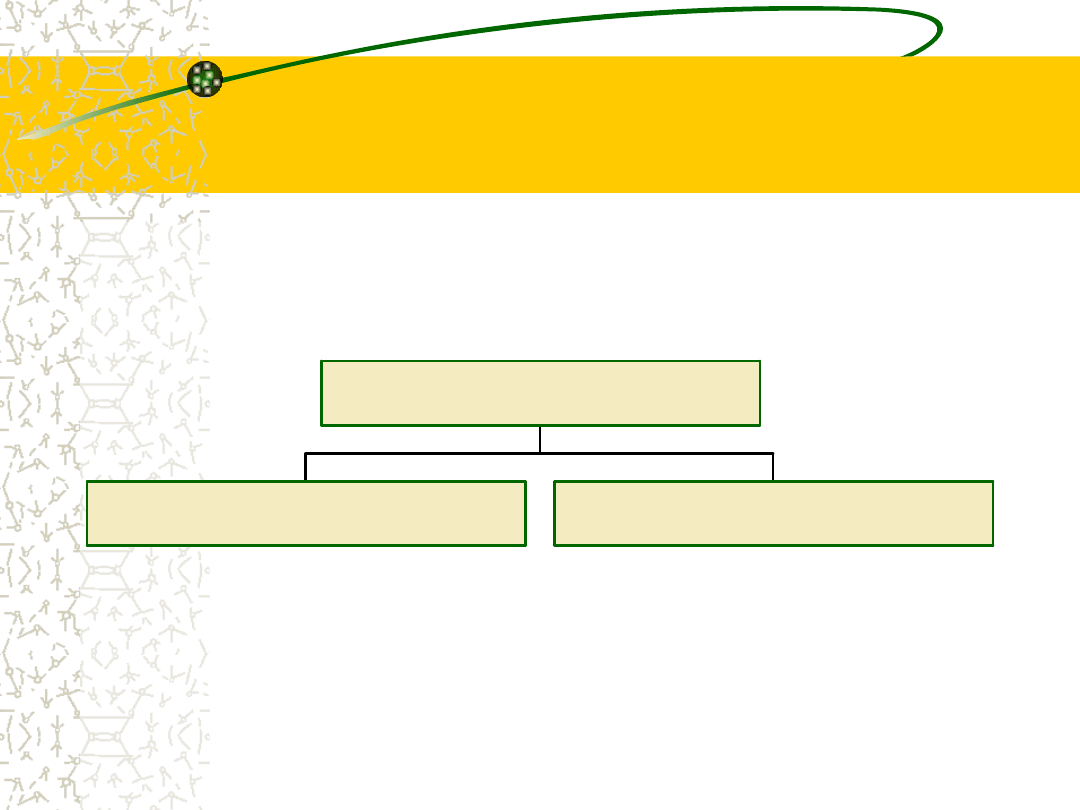
Działy statystyki

S ta ty s t y k a o p i s o w a

W n io s k o w a n i e s t a ty s t y c z n e

S t a ty s t y k a m a te m a ty c z n a

5

Statystyka opisowa

Zajmuje się metodami
gromadzenia, opisu i
przedstawiania danych w postaci
sumarycznej
Opis statystyczny dokonywany jest
za pomocą określonych
charakterystyk (miar)

6

Wnioskowanie

statystyczne

Oparte jest na rachunku
prawdopodobieństwa, będącego działem
matematyki
Zajmuje się - na podstawie prób
statystycznych -szukaniem reguł o
właściwościach populacji i relacjach
między populacjami w celu wyciągania
uogólnionych wniosków o nich.

7

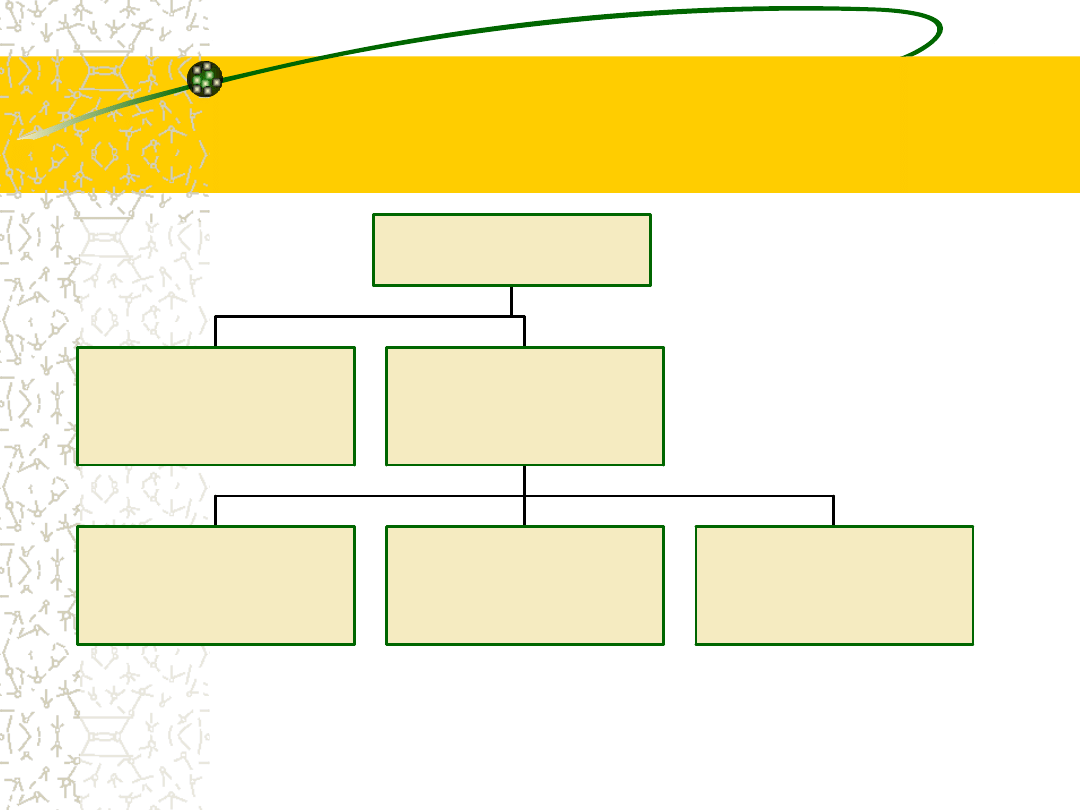
Pojęcia i definicje:

Zbiorowość statystyczna – zbiór elementów

objętych badaniem.
Populacja generalna – zbiór danych liczbowych

charakteryzujących zjawisko.
Próba (populacja próbna) – podzbiór populacji

generalnej.
Jednostka statystyczna – element zbiorowości

statystycznej.
Cecha – właściwość jednostki statystycznej.
Materiał statystyczny – wyniki pomiarów lub

obserwacji z jednostek statystycznych.
Szereg statystyczny – uporządkowany zbiór

wartości cechy.

8

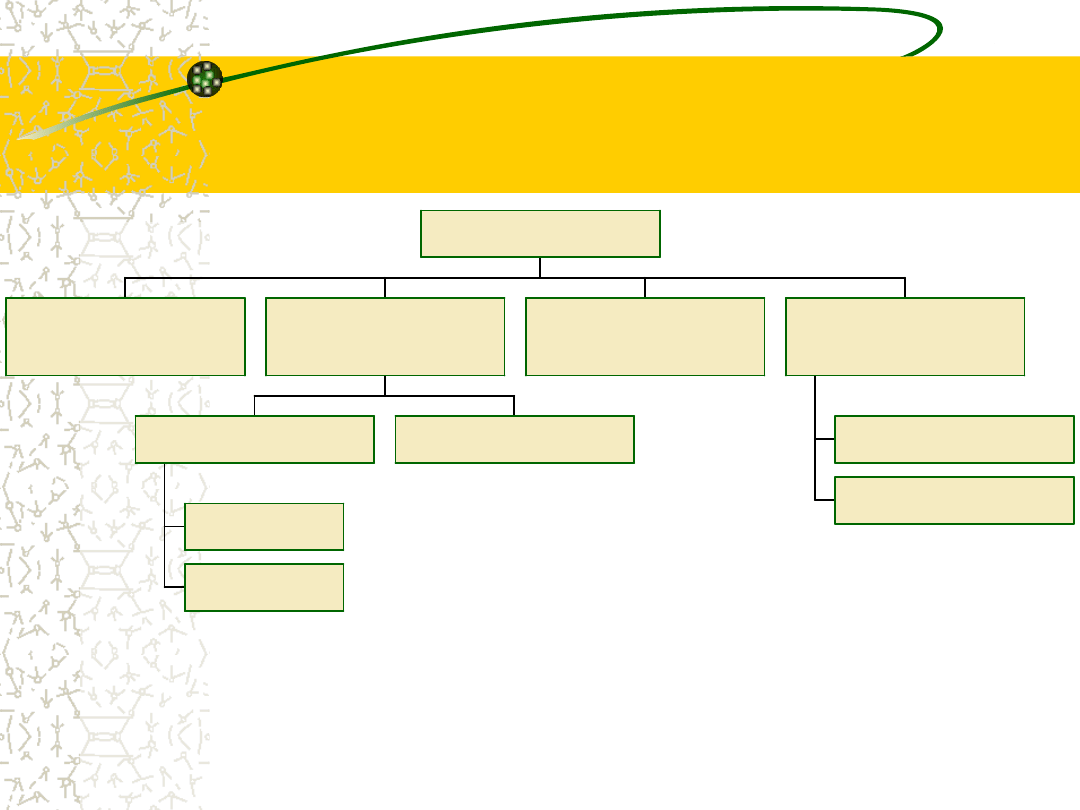
Podział cech

j a k o ś c io w e

( n i e m ie r z a ln e )

c i ą g łe

s k o k o w e

q u a s i - i lo ś c i o w e

( p o r z ą d k o w e )

i lo ś c i o w e

( m i e r z a ln e )

C e c h y

9

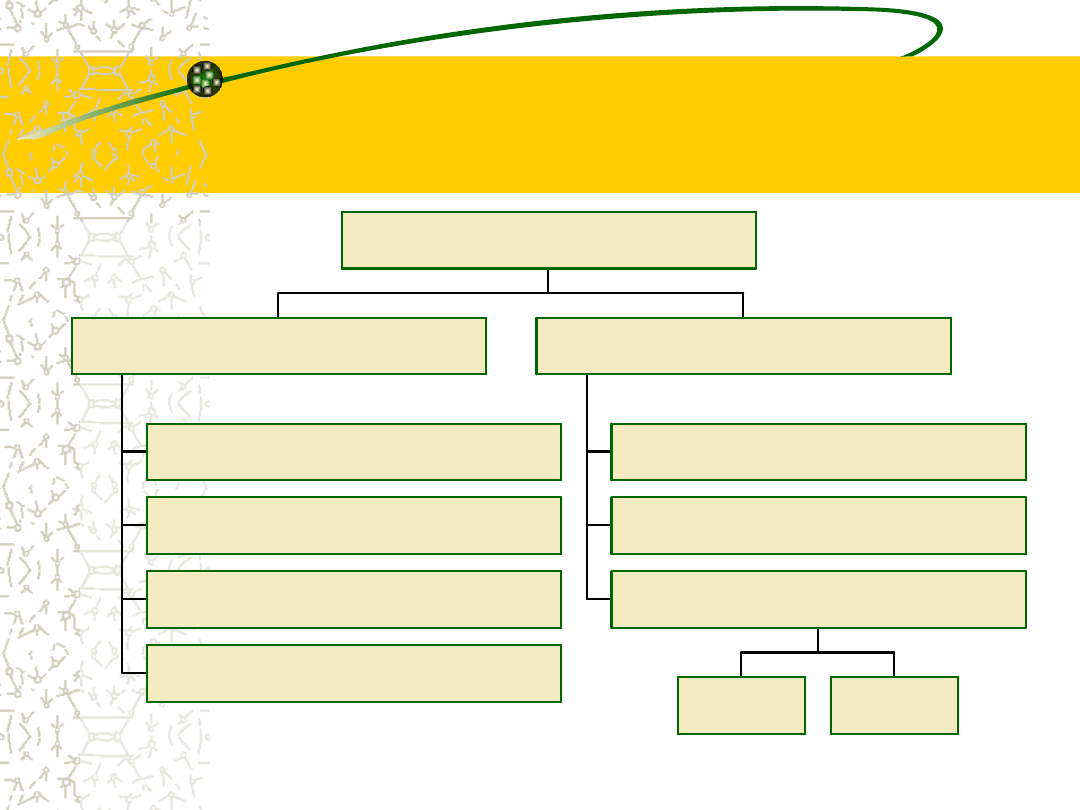
Rodzaje skal pomiarowych

Skala nominalna
Skala porządkowa
Skala przedziałowa
Skala ilorazowa

10

Rodzaje szeregów

statystycznych

s z c z e g ó ło w e
( w y li c z a j ą c e )

p u n k t o w e

p r z e d z ia ło w e

c e c h m i e r z a ln y c h

c e c h n i e m i e r z a ln y c h

r o z d z ie lc z e
( s tr u k t u r a ln e )

p r z e s t r z e n n e
( g e o g r a fi c z n e )

m o m e n t ó w

o k r e s ó w

c z a s o w e
( d y n a m ic z n e )

s z e r e g i s ta t y s t y c z n e

11

Rodzaje charakterystyk

populacji (prób)

Miary skupienia
Miary rozproszenia
Miary kształtu

12

Miary skupienia

(koncentracji)

ś r e d n ia a r y tm e t y c z n a

ś r e d n ia a r y tm a t y c z n a w a ż o n a

ś r e d n i a g e o m e t r y c z n a

ś r e d n i a h a r m o n i c z n a

k la s y c z n e

m o d a ( d o m i n a n t a )

m e d i a n a

k w a r t y le

d e c y le

k w a n t y le

p o z y c y j n e

ś r e d n ie

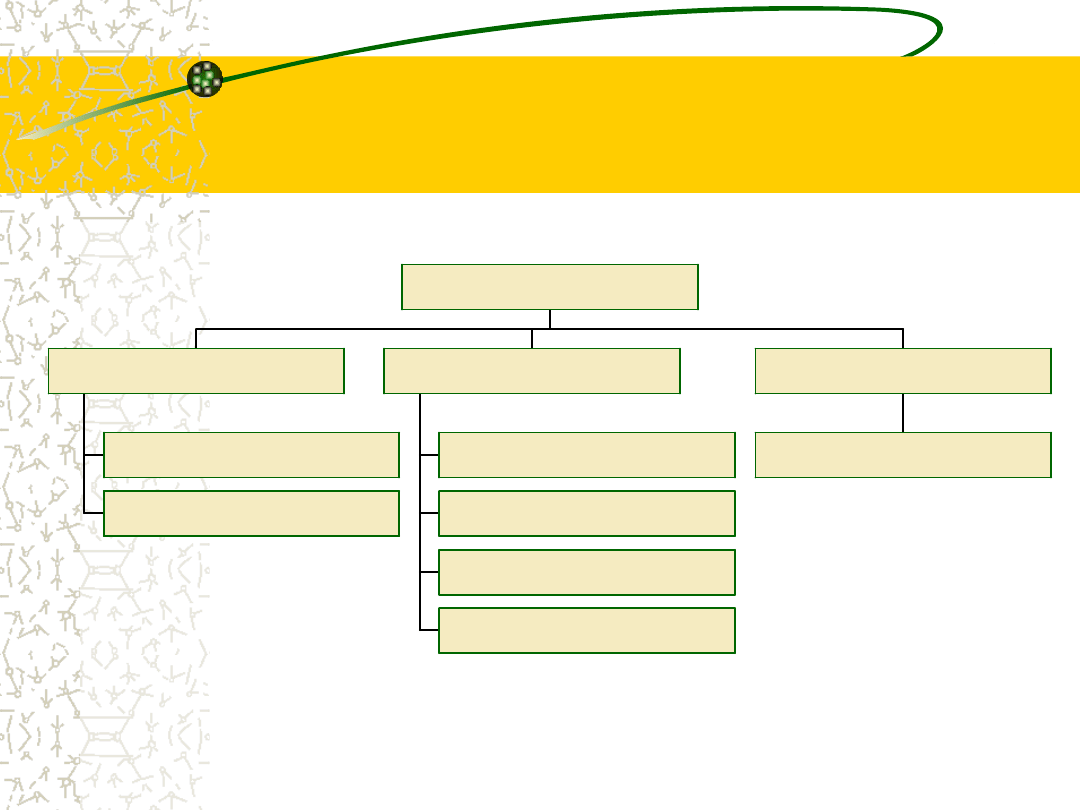
13

Miary rozproszenia

(zmienności, dyspersji)

r o z s te p ( a m p li t u d a w a h a ń )

o d c h y le n i e ć w i a r tk o w e

p o z y c y j n e

o d c h y le n i e p r z e c i ę t n e

o d c h y le n i e s ta n d a r d o w e

w a r ia n c ja

b łą d s t a n d a r d o w y

k la s y c z n e

w s p ó łc z y n n i k z m i e n n o ś c i

m i e s z a n e

m ia r y r o z p r o s z e n ia

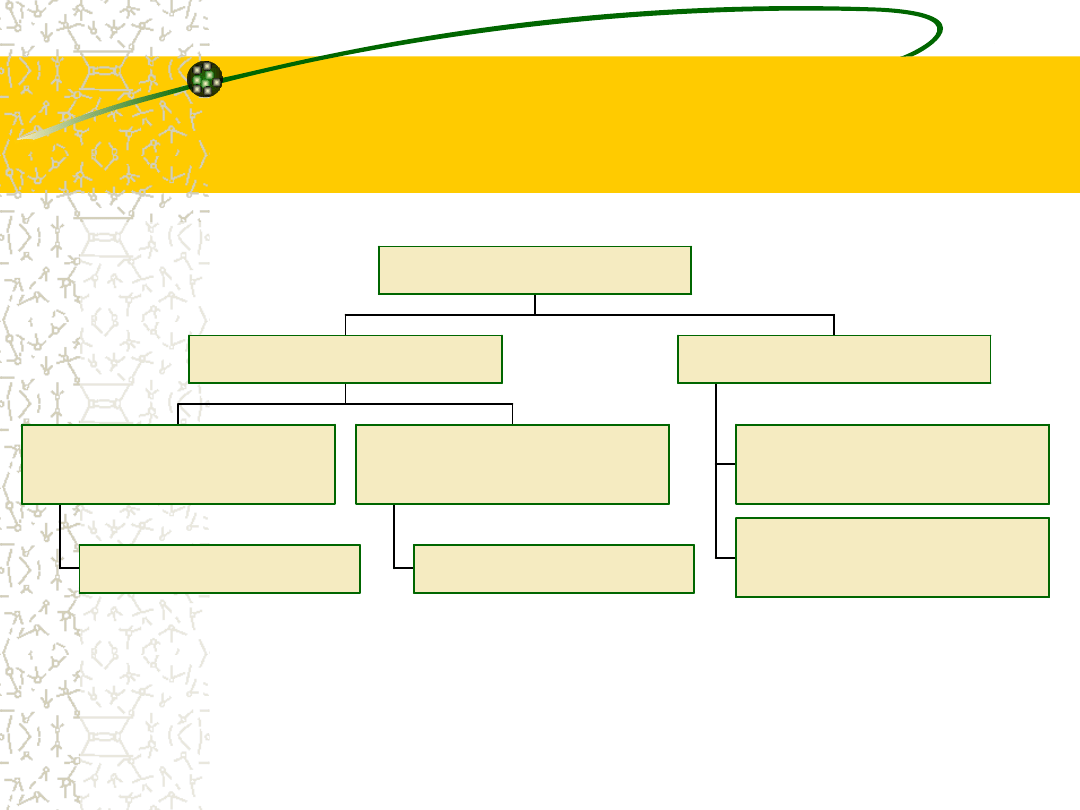
14

Miary kształtu

s k o ś n o ś ć

b e z w z g lę d n e

w s p ó łc z y n n ik s k o ś n o ś c i

w z g lę d n e

m i a r y a s y m e t r ii

w s p ó łc z y n n i k s p ła s z c z e n ia

w s p ó łc z y n n i k k o n c e n t r a c ji

L o r e n z a

m ia r y z r ó ż n ic o w a n ia

m i a r y k s z t a łtu

15

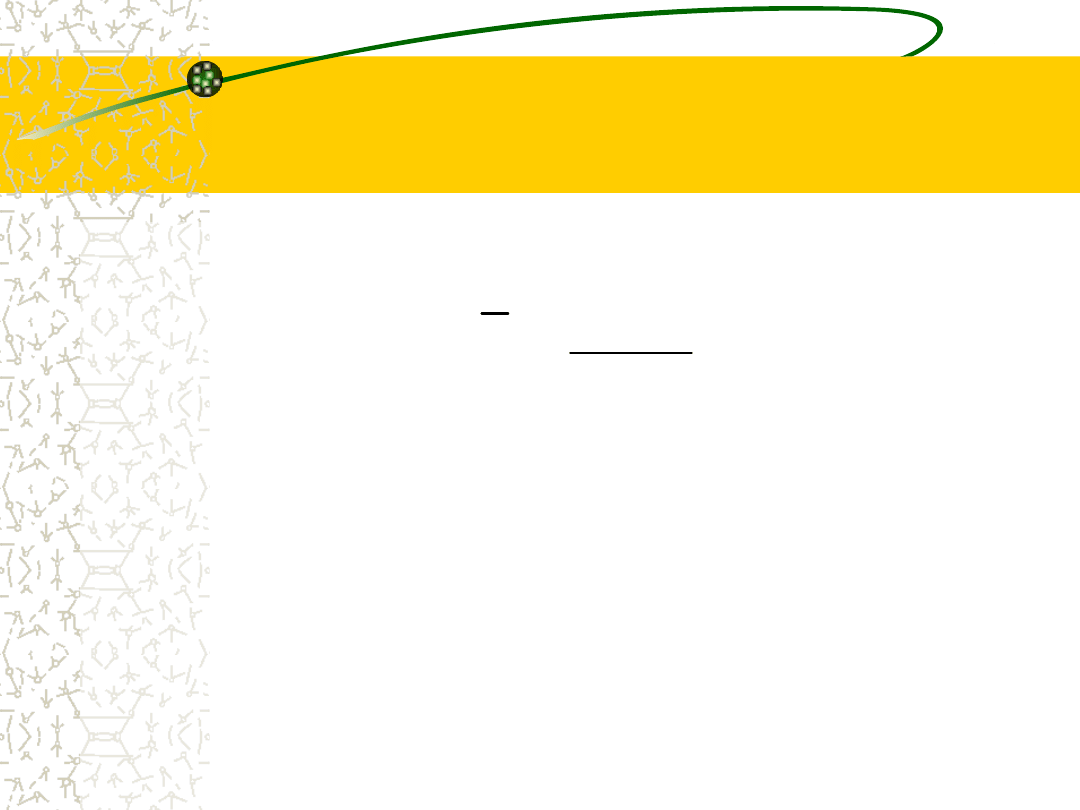
Średnia

arytmetyczna:

n

x

x

n

i

i







1

•

X

min

< średnia < X

max

• Suma odchyleń poszczególnych
wartości zmiennej od średniej
arytmetycznej jest równa 0

16

Średnia arytmetyczna c.d.

•Jeżeli każdą z wartości szeregu liczbowego
zwiększymy (zmniejszymy, podzielimy,
pomnożymy) o stałą, to średnia arytmetyczna
będzie równa sumie (różnicy, ilorazowi,
iloczynowi) średniej arytmetycznej pierwotnych
danych i tej stałej.

•Na wartość średniej arytmetycznej duży
wpływ mają wartości skrajne
(ekstremalne)

17

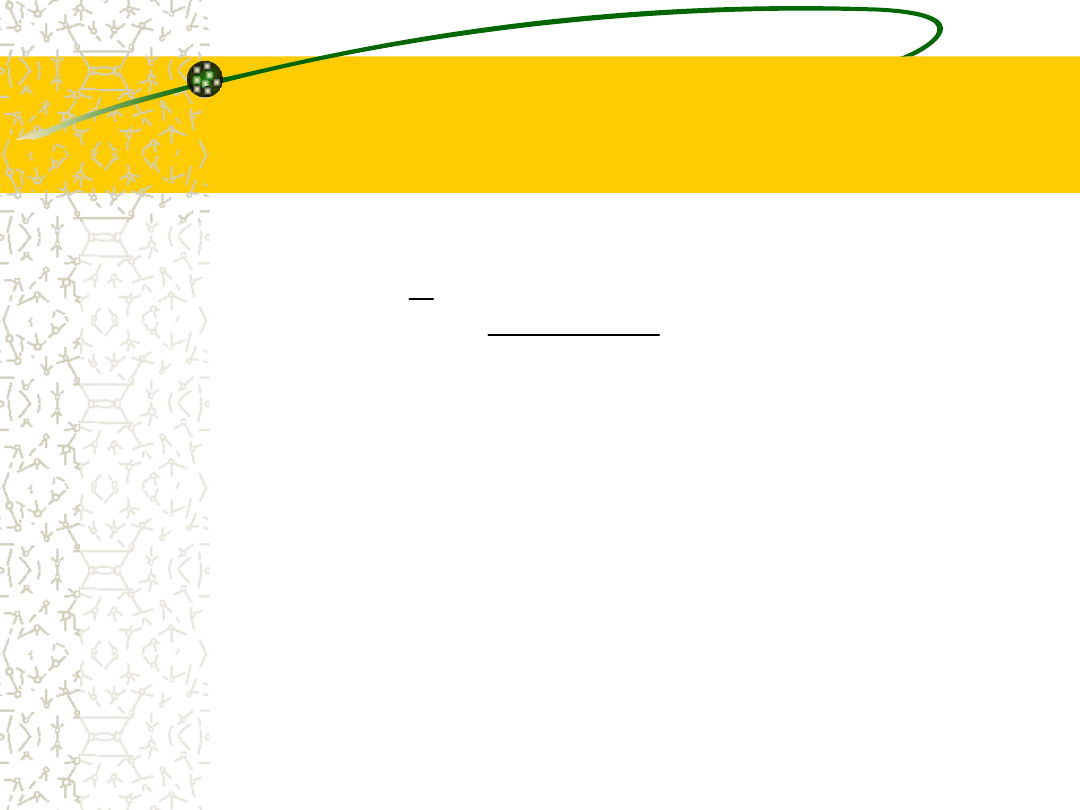
Średnia arytmetyczna

ważona:

•Jest stosowana, gdy warianty zmiennej (x

i

)

występują z różną częstotliwością. Wtedy
poszczególnym wariantom odpowiadają różne
liczebności tzw. wagi (f

i

).







i

i

i

f

f

x

x

·

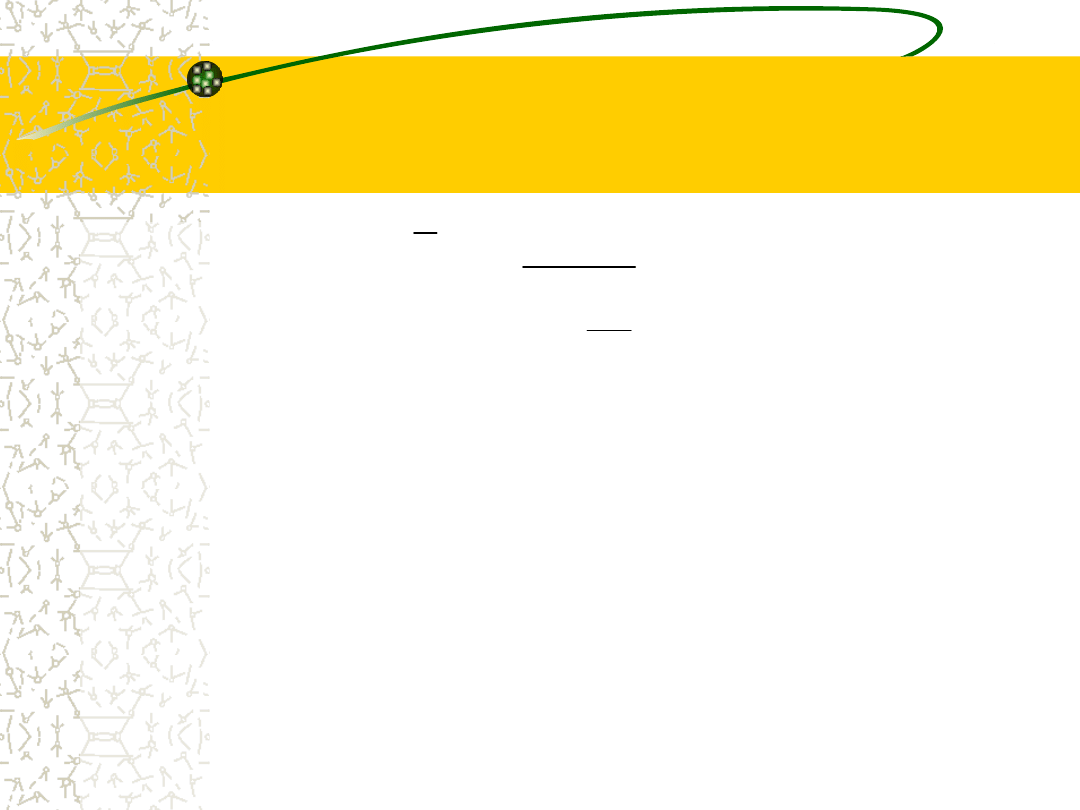
18

Średnia harmoniczna

•Średnią tą stosujemy przy wyliczaniu
średniego tempa zjawisk, gdy mamy do
czynienia z wielkością stosunkową w której
zmienny jest mianownik. Jako wielkość
stosunkową rozumiemy stosunek dwóch
różnych wielkości (każda z nich mogłaby być
niezależnie analizowana) np. wydajność pracy,
prędkość, gęstość zaludnienia.





i

H

x

n

x

1

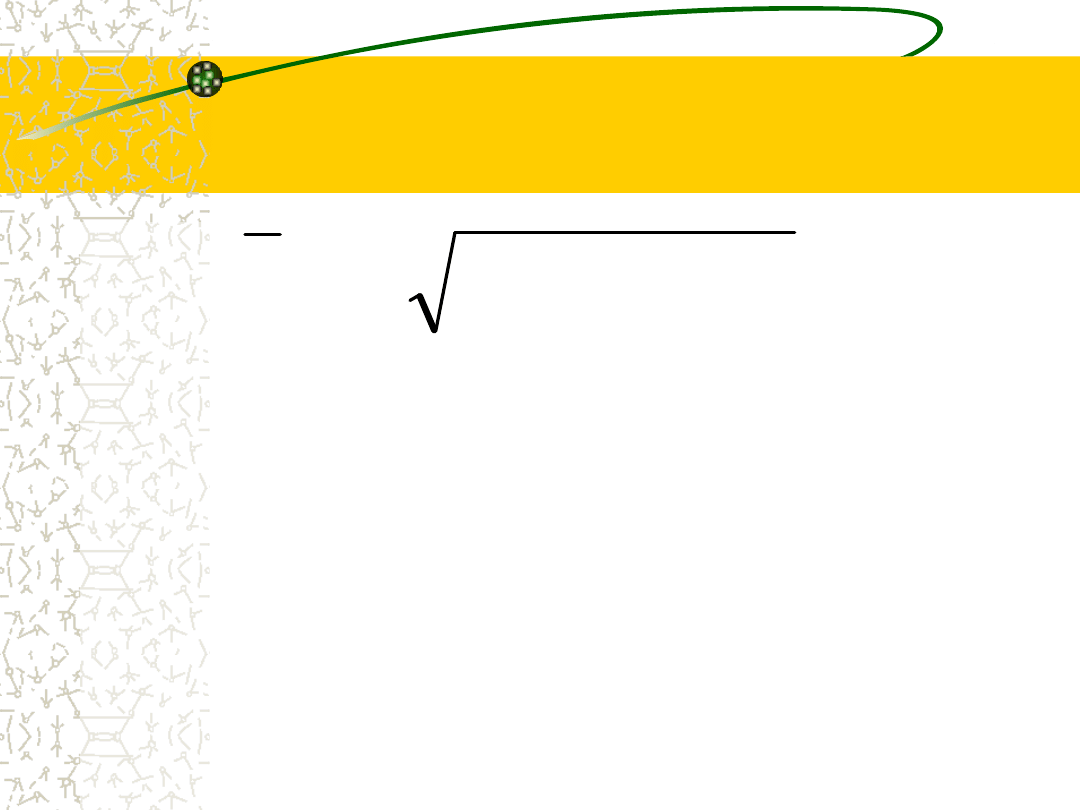
19

Średnia geometryczna

n

n

G

x

x

x

x

·....·

·

2

1



•Średnią tą stosujemy przy wyliczaniu średniej
z szeregów dynamicznych (czasowych), cech
przedstawionych w liczbach względnych

•Średnia ta jest mniej wrażliwa na wartości
skrajne.

średnia arytmetyczna > średnia
geometryczna > średnia harmoniczna

20

Moda (dominanta,

wartość najczęstsza)

•W przypadku cechy liczbowej skokowej jest to
wartość powtarzająca się najczęściej.

•W przypadku cechy liczbowej ciągłej jest to
wartość, wokół której jest najwyższa
koncentracja (gęstość) wyników.

Mo

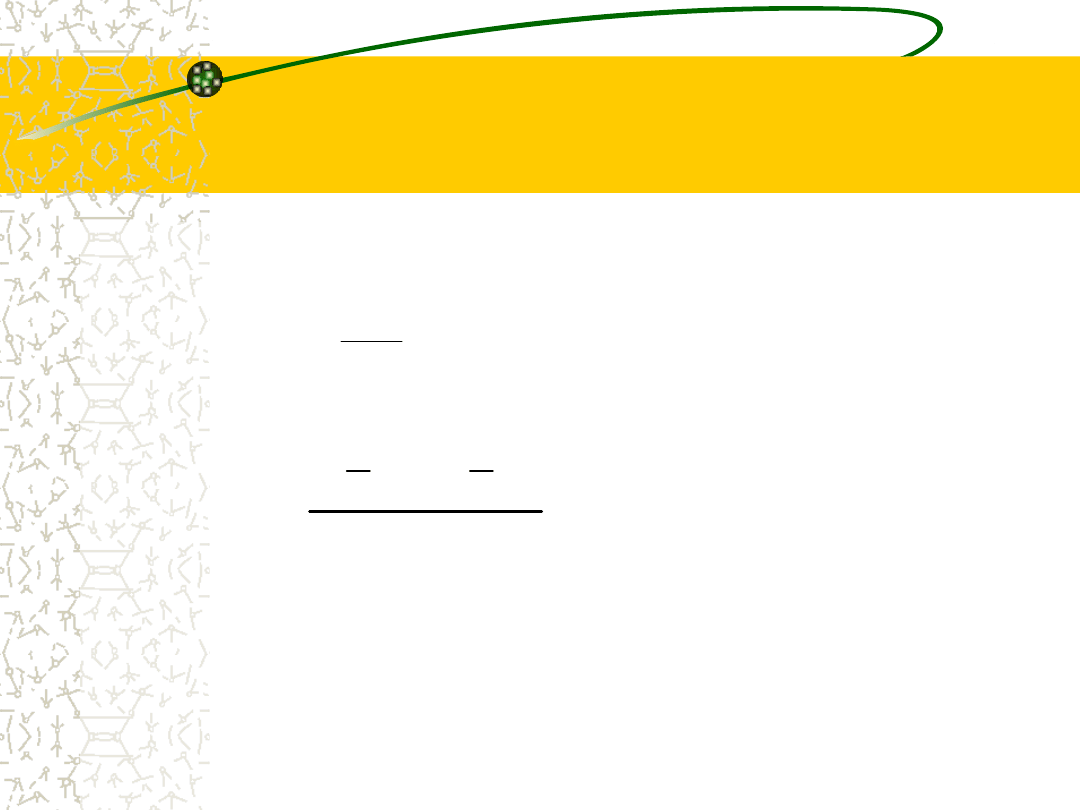
21

Mediana (wartość

środkowa)

•Jest to wartość środkowa uporządkowanego
szeregu liczbowego.

parzyste

gdy

2

e

nieparzyst

gdy

1

2

2

2

1

n

x

x

Me

n

x

Me

n

n

n











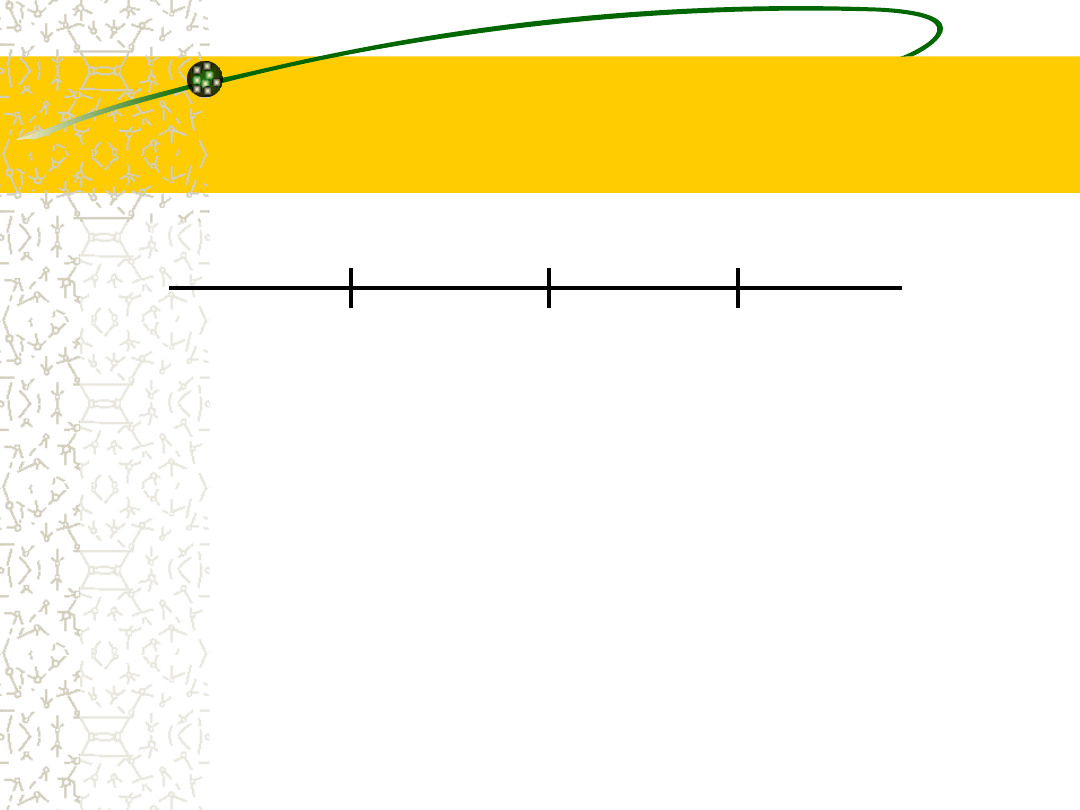
22

Kwartyle

•dzielą uporządkowany szereg liczbowy na
cztery równe części

•drugi kwartyl jest jednocześnie medianą

•pierwszy kwartyl jest „medianą pierwszej
połowy szeregu”

•trzeci kwartyl jest „medianą drugiej połowy
szeregu”

Me

Q

2

Q

1

Q

3

x

min

x

max

23

Rozstęp (amplituda

wahań)

Klasyczny

Kwartylowy

1

3

min

max

Q

Q

R

x

x

R









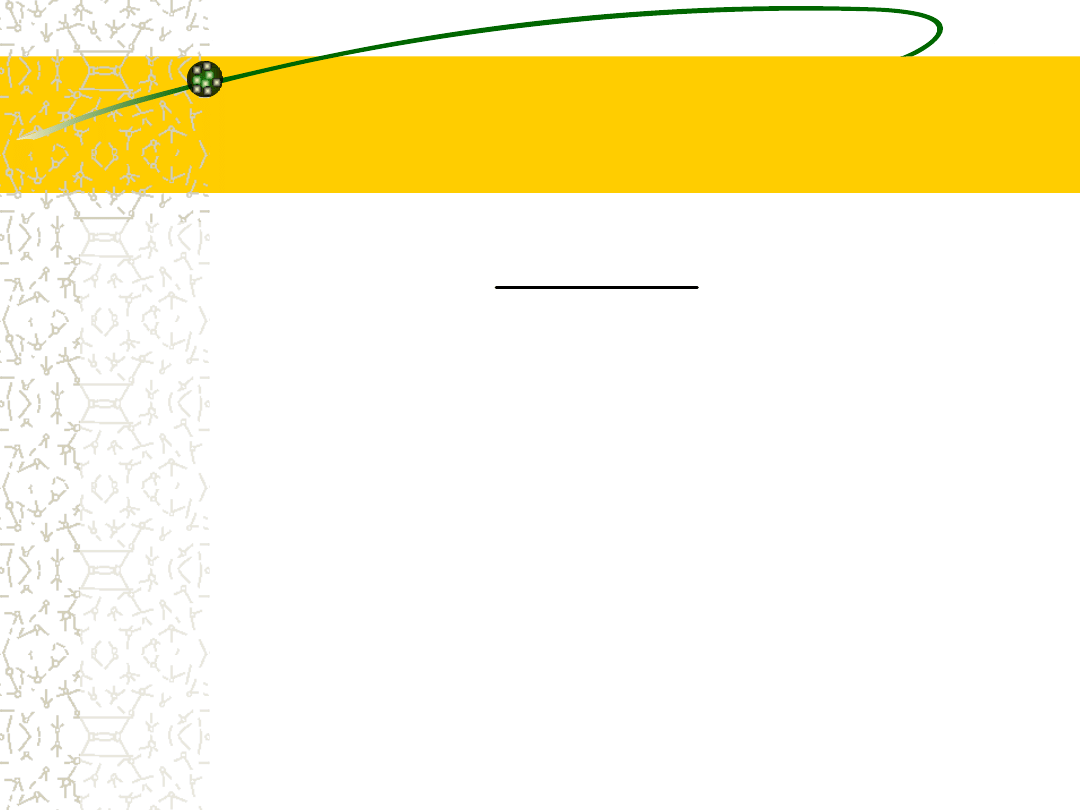
24

Odchylenie ćwiartkowe

2

1

3

Q

Q

Q





•Określa poziom zróżnicowania części szeregu
liczbowego po odrzuceniu skrajnych 25 %
obserwacji. Oznacza to, że odchylenie
ćwiartkowe określa średnią rozpiętość wartości
cechy w dwóch wewnętrznych ćwiartkach
zbiorowości.

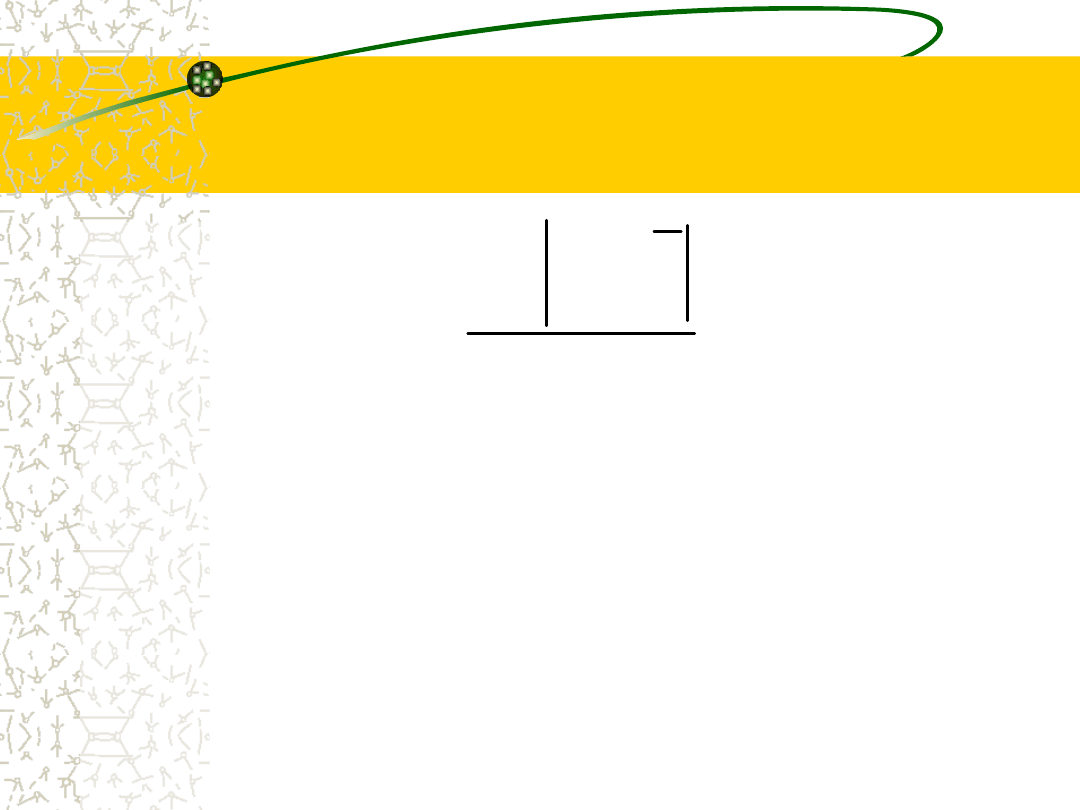
25

Odchylenie przeciętne

n

x

x

d

i







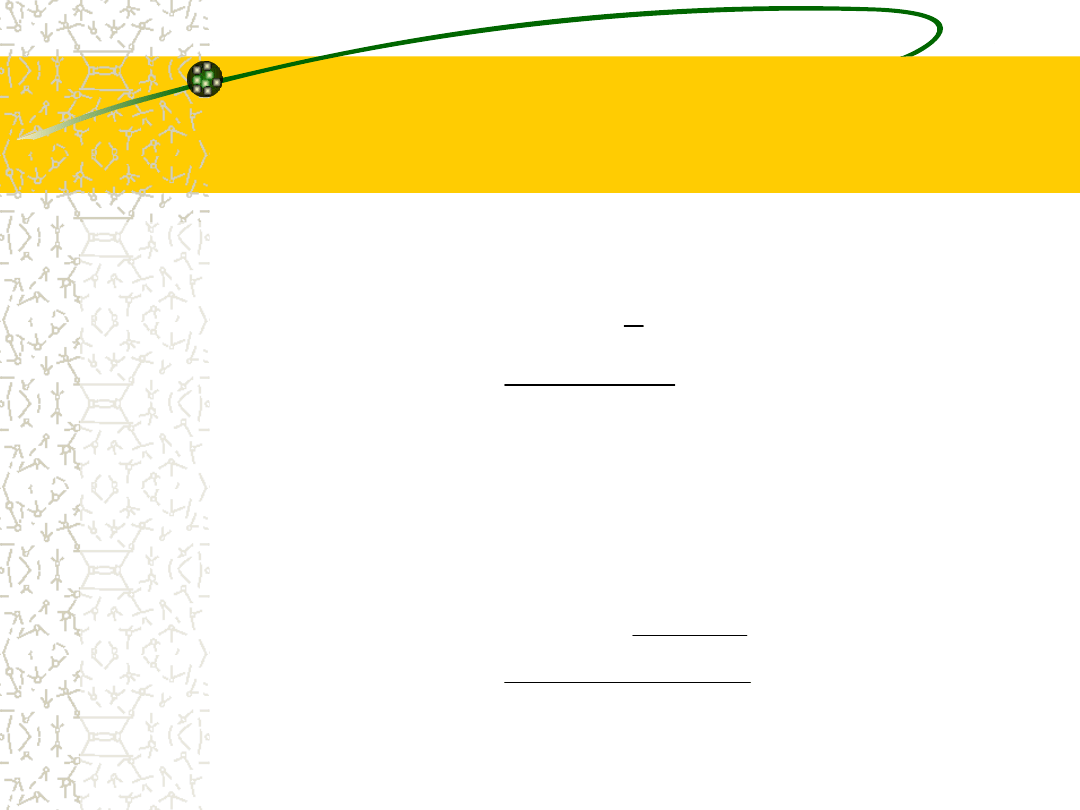
26

Wariancja

 

 

1

1

2

2

2

2

2



















n

n

x

x

s

n

x

x

s

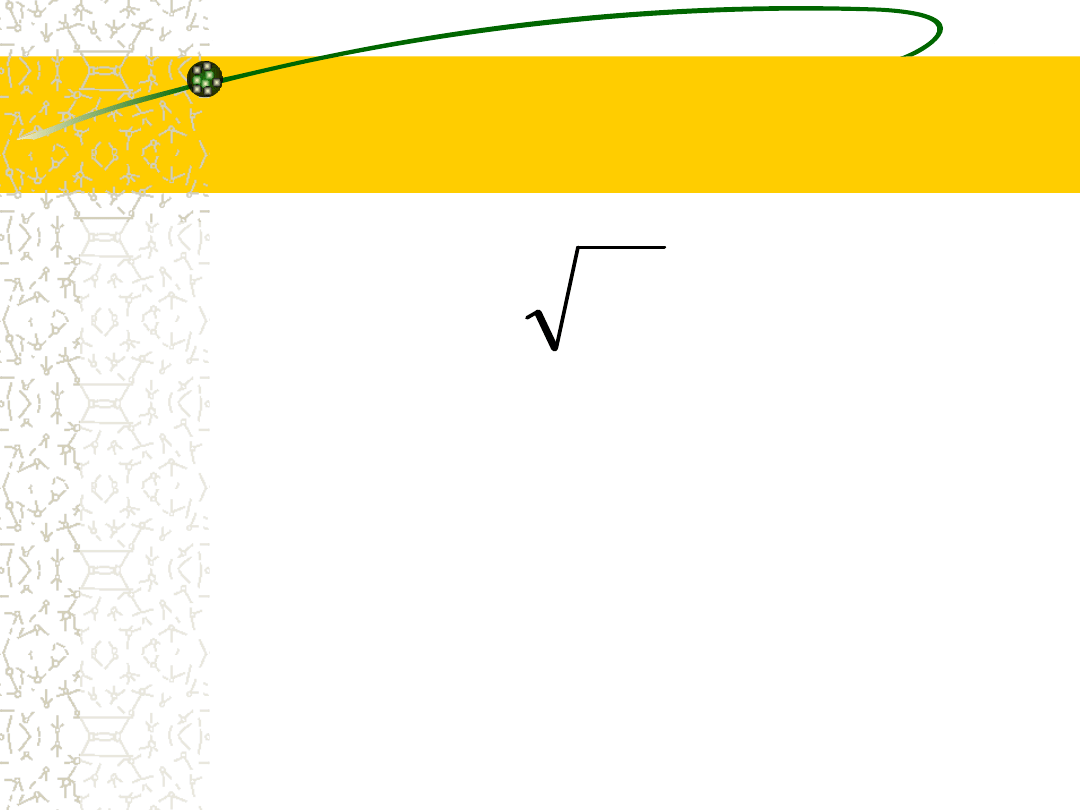
27

Odchylenie standardowe

2

s

s 

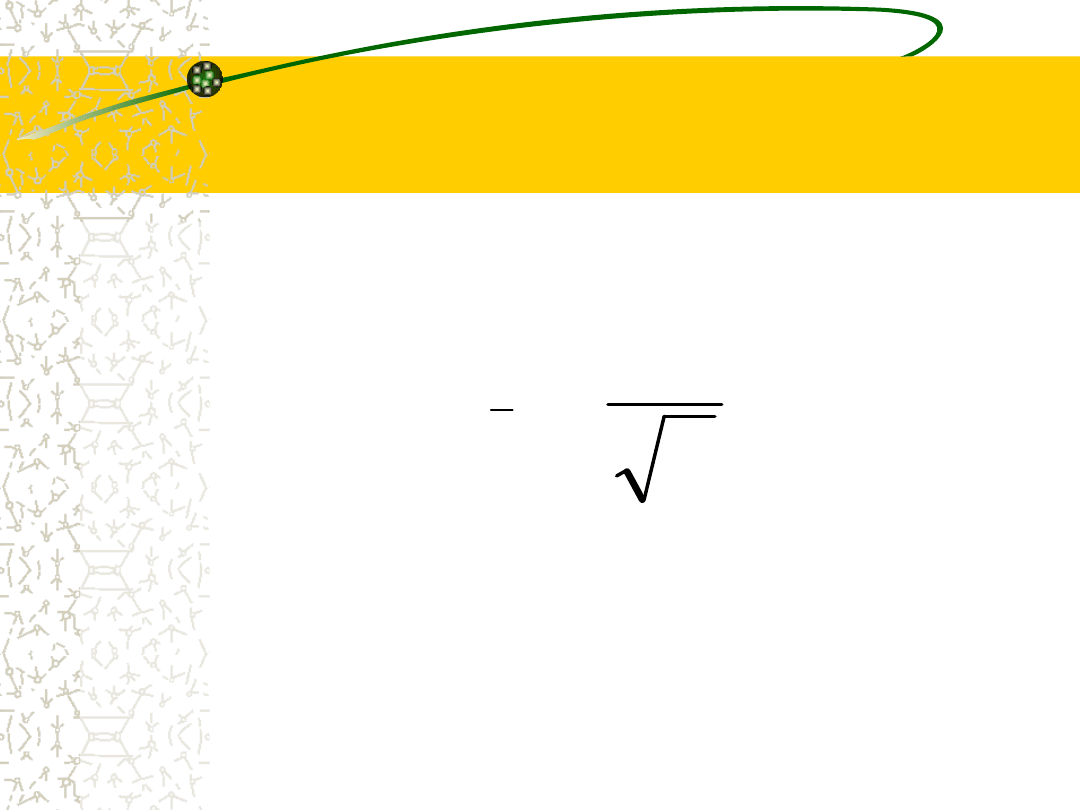
28

Błąd standardowy (błąd
średniej arytmetycznej)

n

s

s

x



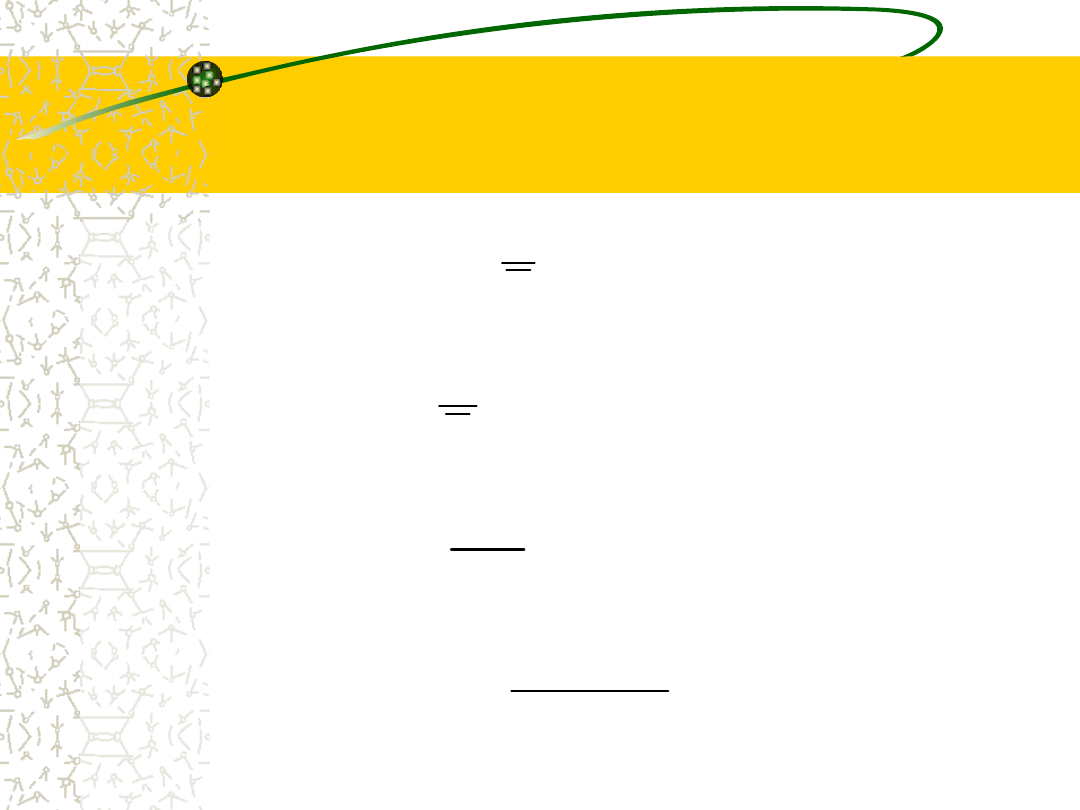
29

Współczynnik zmienności

(4)

V

(3)

%

100

V

(2)

%

100

)

1

(

%

100

(%)

1

3

1

3

Q3

-

Q1

Q

Q

Q

Q

Q

Me

Q

x

d

V

x

s

V

d













30

Współczynnik zmienności

c.d.

• określa stopień zróżnicowania wyników w

stosunku do średniej

• wyliczony ze wzorów (1) i (2) jest określany

jako klasyczny

• wyliczony ze wzorów (3) i (4) jest określany

jako pozycyjny

• wykorzystywany jest do:
a) określania ścisłości wykonania

doświadczenia

b) porównania stopnia zmienności kilku cech w

obrębie jednej populacji

c) porównania stopnia zmienności tej samej

cechy w obrębie kilku populacji

31

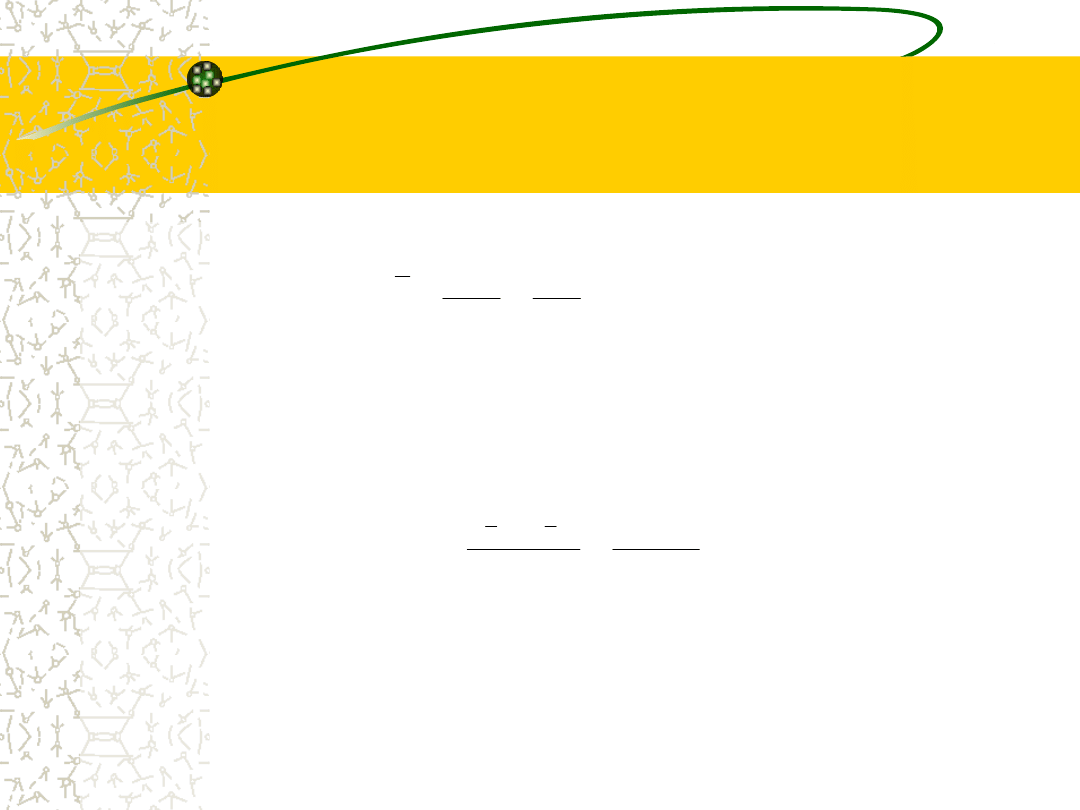
Przykład 1

Scharakteryzować

długość

kłosa

pszenżyta

ozimego odmiany Lamberto.
Pobrano próbę o liczebności n=10

kłosów i

uzyskano następujące wyniki (cm):
21; 20; 19; 15;17; 19; 17; 18; 18; 16.

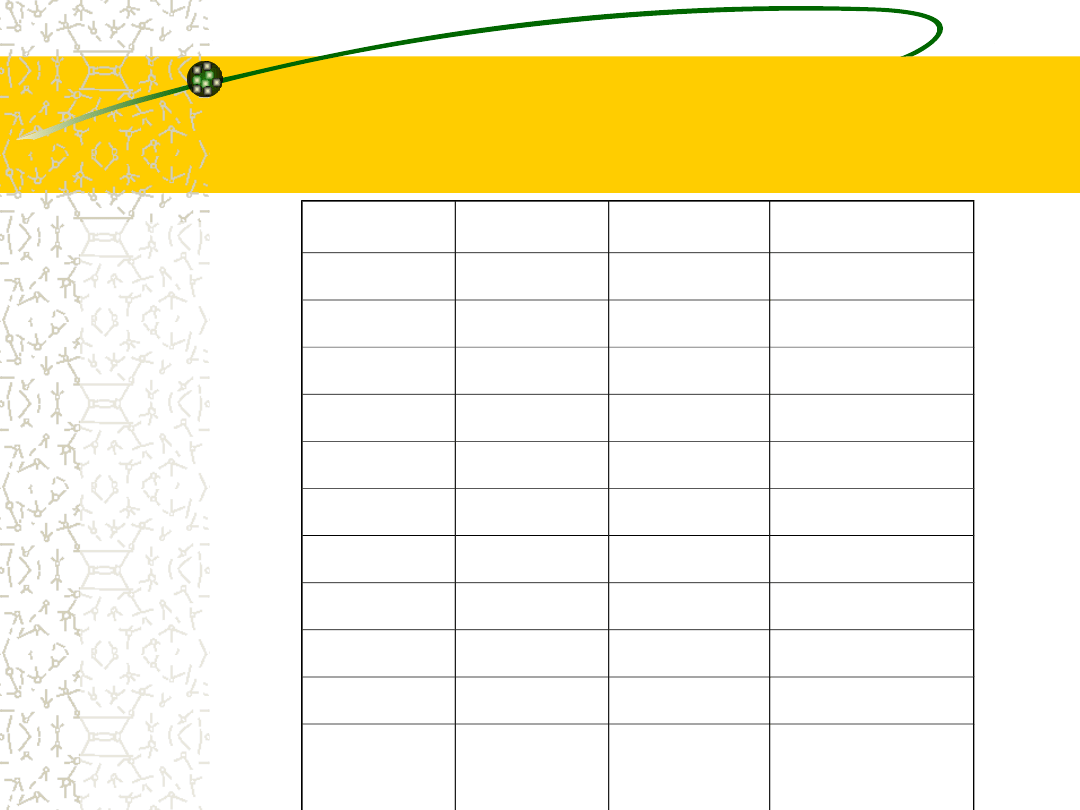
32

Tabela z wynikami i obliczeniami

pośrednimi

i

x

i

x

i

2

|x

i

-x

śr

|

1

21

441

3

2

20

400

2

3

19

361

1

4

15

225

3

5

17

289

1

6

19

361

1

7

17

289

1

8

18

324

0

9

18

324

0

10

16

256

2

x

i

=

180

x

i

2

=327

0



|x

i

-x

śr

|=14

33

Miary skupienia

cm

Q

cm

Q

cm

Q

cm

x

x

Me

cm

Mo

cm

n

x

x

n

n

19

18

17

18

2

18

18

2

19

;

18

;

17

21

;

20

;

19

;

19

;

18

;

18

;

17

;

17

;

16

;

15

18

10

180

3

2

1

1

2

2





























34

Miary rozproszenia

cm

n

s

s

x

s

V

cm

s

s

cm

n

n

x

x

s

cm

n

x

x

d

cm

Q

Q

Q

cm

Q

Q

R

cm

x

x

R

x

577

,

0

10

83

,

1

%

2

,

10

100

18

83

,

1

(%)

100

83

,

1

33

,

3

33

,

3

1

10

10

180

3270

1

40

,

1

10

14

1

2

17

19

2

2

17

19

6

15

21

2

2

2

2

2

2

1

3

1

3

min

max





































































































35

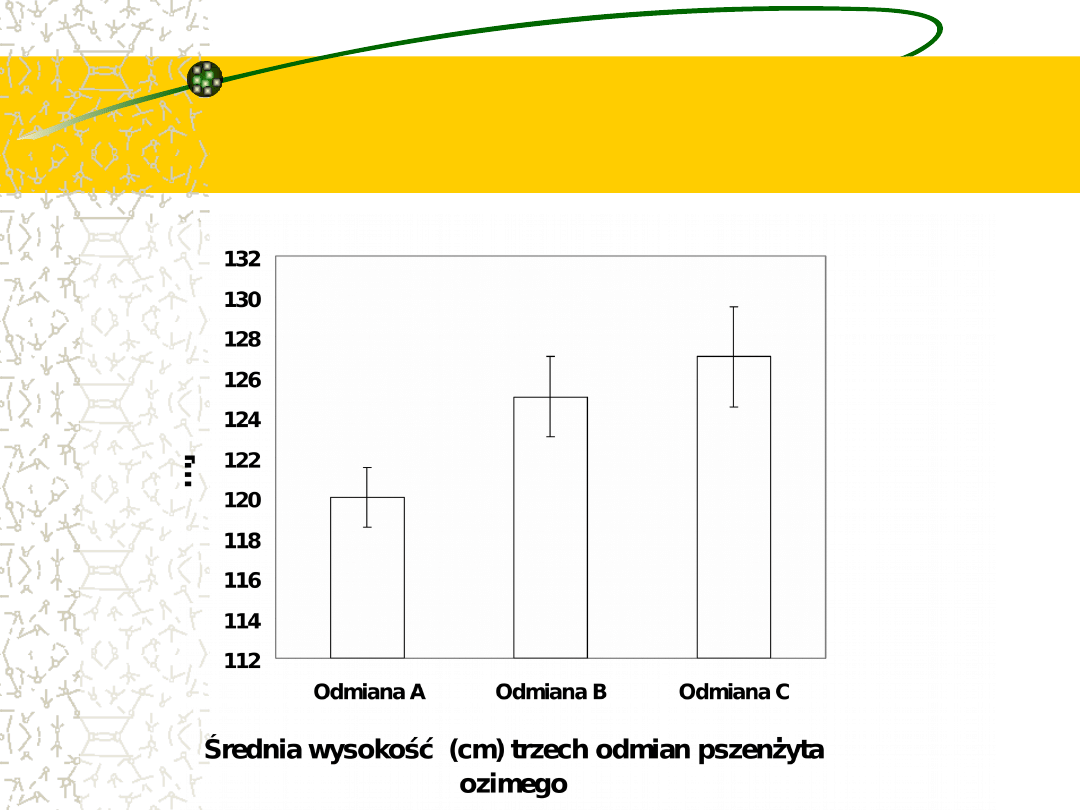
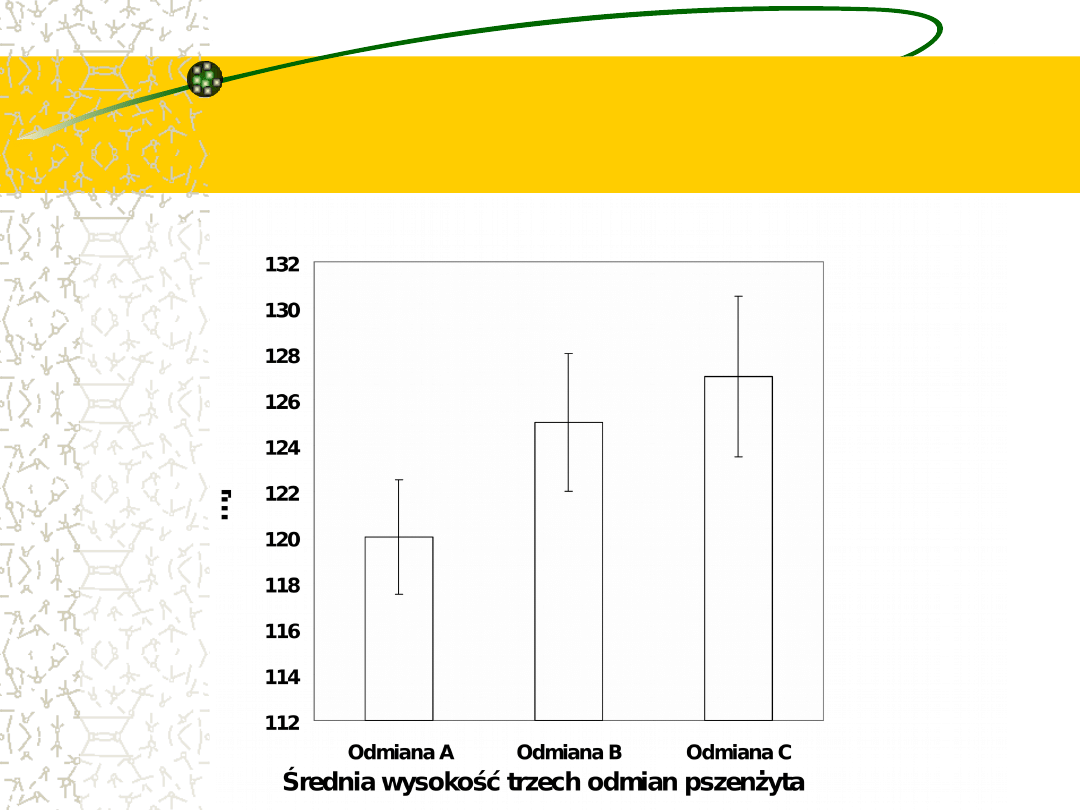
Przykład 2

Badano wysokość roślin trzech odmian pszenżyta
(A,B,C). Pobrano próby n=10 roślin każdej
odmiany. Wyliczono średnie i odchylenia
standardowe i uzyskano następujące wyniki w cm:

Odmian

a A

Odmian

a B

Odmian

a C

120

125

127

s

1,5

2

2,5

x

36

37

Przykład 3

Badano wysokość roślin trzech odmian
pszenżyta (A,B,C). Pobrano próby n=10 roślin
każdej odmiany. Wyliczono średnie i
odchylenia standardowe i uzyskano
następujące wyniki w cm:

Odmian

a A

Odmian

a B

Odmian

a C

120

125

127

s

2,5

3,0

3,5

x

38

39

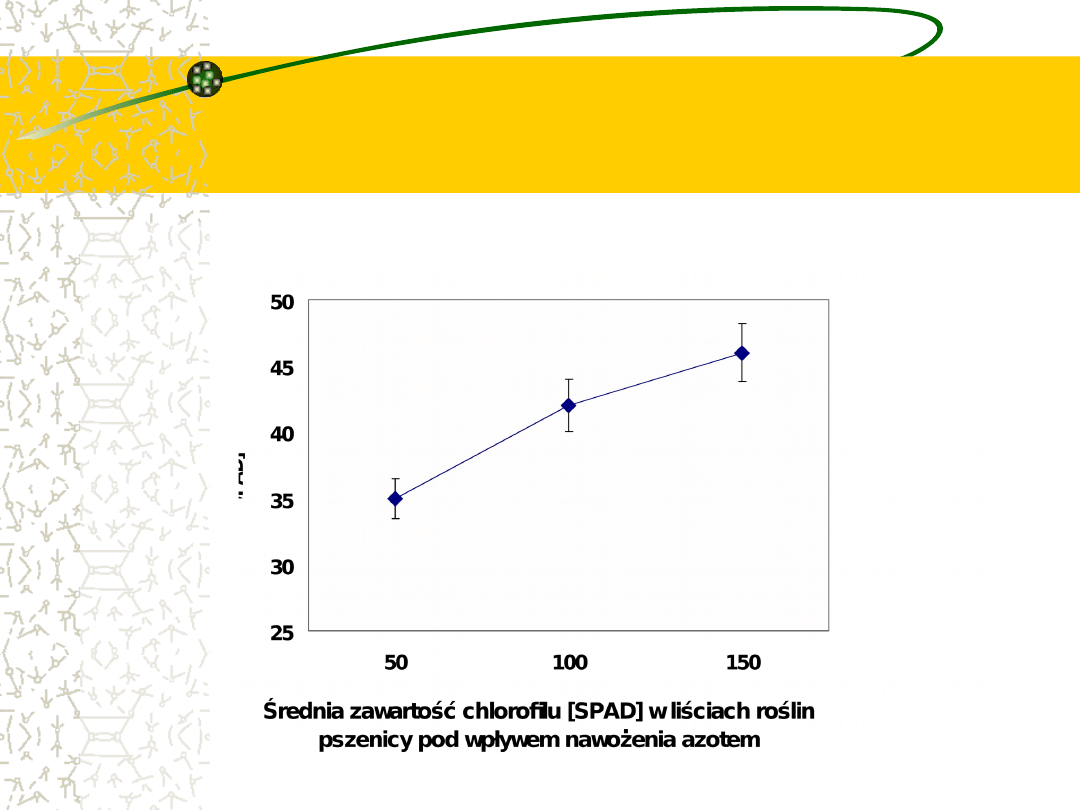
Przykład 4

Badano zawartość chlorofilu przy użyciu

chlorofilometru SPAD 502 na roślinach pszenicy

nawożonych trzema dawkami azotu (50, 100, 150

kg N/ha). Dla każdej dawki azotu wykonano n=20

pomiarów. Wyliczono średnie i odchylenia

standardowe i uzyskano następujące wyniki:

50

100

150

35

42

46

s

1,5

2,0

2,2

x

40