Przykłady szeregów, dla których nie można przeprowadzić pełnej analizy struktury.

Przykład 1.

Bezrobotni zarejestrowani w 2006 r. w powiecie wągrowieckim według wieku

(stan na 31.12.)

Wiek w latach	Liczba bezrobotnych	Odsetek bezrobotnych	Kumulowany odsetek
24 i mniej 25 - 34 35 - 44 45 - 54 55 więcej	1243 1332 960 993 198	26,30 28,18 20,32 21,01 4,19	26,30 54,48 74,80 95,81 100,00
Ogółem	4726	100,00	X

W tym przypadku można wyliczyć tylko medianę i kwartyl 3.

Kwartyl 1 nie może być wyliczony, gdyż znajduje się w pierwszym przedziale, a ten przedział jest otwarty, czyli nie ma jednoznacznie określonej rozpiętości.

Przykład 2.

Bezrobotni zarejestrowani w powiecie gnieźnieńskim w roku 2006 według czasu pozostawania na bezrobociu.

Czas pozostawania na bezrobociu w miesiącach	Liczba bezrobotnych	Odsetek bezrobotnych	Kumulowany odsetek
1 i mniej 1 - 3 3 - 6 6 - 12 12 - 24 powyżej 24	669 1015 1113 1593 1257 3349	7,44 11,28 12,37 17,71 13,97 37,23	7,44 18,72 31,09 48,80 62,77 100,00
Ogółem	8996	100,00	X

W tym zadaniu można wyliczyć tylko kwartyl 1 i medianę. Tu kwartyl 3 jest w przedziale ostatnim, który jest otwarty, czyli nie ma jednoznacznie określonej rozpiętości.

Przykład 3.

Pracownicy firmy „Z” w Poznaniu według wieku (stan na 1.03.2008 r.)

Wiek w latach	Liczba pracowników	Skumulowana liczebność	Odsetek pracowników
xi	ni	kum ni	wi
20 - 30 30 - 40 40 - 50 50 - 60 powyżej 60	15 25 48 30 6	15 40 88 118 124	12,10 20,16 38,71 24,19 4,84
Ogółem	124	X	100,00

W tym przypadku można zastosować parametry klasyczne, po umownym zamknięciu ostatniego przedziału tak, aby miał identyczną rozpiętość, jak wszystkie wcześniejsze przedziały.

Umowne zamknięcie przedziału jest dopuszczalne tylko wtedy, gdy w tym przedziale znajduje się mało jednostek - umownie zakłada się, że nie może być ich więcej niż 5% ogólnej ich liczby.

Przykład 4.

Przedsiębiorstwa budowlane w Polsce w roku 2007 według liczby pracujących

Liczba pracujących	Liczba przedsiębiorstw	Odsetek przedsiębiorstw
19 osób i mniej 20 - 49 50 - 99 100 - 499 500 osób i więcej	202822 2765 936 636 64	97,88 1,33 0,45 0,31 0,03
Ogółem	207223	100,00

W tym zadaniu nie można wyliczyć żadnego parametru.

Zadanie:

Przeprowadzono analizę indywidualnych gospodarstw rolnych w pewnej gminie w województwie wielkopolskim w czerwcu 2007 roku według powierzchni użytków rolnych w ha. Otrzymano następujący szereg rozdzielczy.

W oparciu o podane informacje:

1. Określ zbiorowość, jednostkę i badaną cechę statystyczną.

2. Przeprowadź kompleksową analizę struktury badanych gospodarstw według powierzchni użytków w ha.

3. Badany szereg przedstaw graficznie.

Powierzchnia użytków rolnych w ha	Odsetek gospodarstw
1,01 - 1,99 2,00 - 4,99 5,00 - 6,99 7,00 - 9,99 10,00 - 14,99 15,00 i więcej	15,2 36,0 23,5 15,8 7,1 2,4
Ogółem	100,0

Źródło: Dane umowne.

Rozwiązanie:

ad a)

Zbiorowość statystyczna - indywidualne gospodarstwa rolne w jednej z gmin województwa wielkopolskiego w czerwcu 2007 roku,

jednostka statystyczna - pojedyncze gospodarstwo,

badana cecha - powierzchnia użytków w ha - cecha mierzalna, ciągła.

ad b)

Przedziały klasowe mają różną rozpiętość, ostatni przedział jest otwarty - stąd też nie możemy stosować miar klasycznych. Musimy ograniczyć się do miar pozycyjnych.

Należy w tabeli skumulować odsetek:

Powierzchnia użytków w ha	Odsetek gospodarstw	Odsetek skumulowany
1,01 - 1,99	15,2	15,2
2,00 - 4,99	36,0	51,2
5,00 - 6,99	23,5	74,7
7,00 - 9,99	15,8	90,5
10,00 - 14,99	7,1	97,6
15,00 i więcej	2,4	100,0

Obliczamy wartość mediany:

Ponieważ liczebności są wyrażone w odsetkach, stąd N = 100, w takim razie pozycja mediany to: N/2, czyli 50.

Tak więc mediana jest zawarta w przedziale <2,00 ; 4,99 >.

Korzystamy ze wzoru:




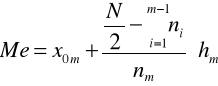
Po podstawieniu otrzymujemy:




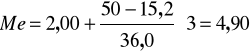
Połowa indywidualnych gospodarstw rolnych w badanym powiecie miała powierzchnię mniejszą od 4,9 ha, a połowa miała powierzchnię przekraczającą 4,9 ha.

Obliczamy kwartyle:

Kwartyl pierwszy dzieli zbiorowość na dwie części w ten sposób, że 25 % jednostek ma wartości mniejsze od tego kwartyla, a 75 % jednostek ma wartości od niego większe.

W przypadku gdy liczebności są wyrażone w odsetkach to kwartyl I ma pozycję N/4, czyli 25. Jest więc w przedziale < 2,00 ; 4,99 >.

Wzór interpolacyjny:




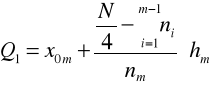
Po podstawieniu otrzymujemy:




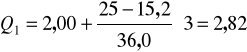
Tak więc, 25 % gospodarstw ma powierzchnię mniejszą od 2,82 ha a 75 % gospodarstw ma powierzchnię ponad 2,82 ha.

Kwartyl trzeci dzieli zbiorowość na dwie części w ten sposób, że 75 % jednostek ma wartości mniejsze od tego kwartyla a 25 % jednostek ma wartości od niego większe.

Pozycja kwartyla trzeciego to 3N/4, czyli w przypadku odsetek 75.

Kwartyl ten jest więc w przedziale <7,00 ; 9,99 >.

Wzór interpolacyjny:




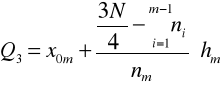
Po podstawieniu otrzymujemy:




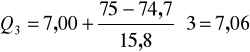
Znaczy to, że 75 % gospodarstw w badanej gminie miało powierzchnię poniżej 7,06 ha a tylko 25 % gospodarstw miało powierzchnię przekraczającą 7,06 ha.

Obliczamy odchylenie ćwiartkowe:




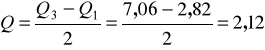
Przeciętne zróżnicowanie powierzchni w badanych gospodarstwach rolnych wynosi 2,12 ha.

Obliczamy pozycyjny współczynnik zmienności:




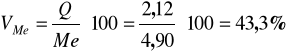
Zróżnicowanie powierzchni jest stosunkowo silne, odchylenie ćwiartkowe stanowi 43,3% mediany.

Obliczamy współczynnik asymetrii:




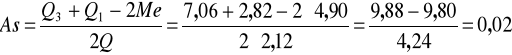
Rozkład powierzchni gospodarstw charakteryzuje się niewielką asymetrią prawostronną.

ad c) Sporządzamy wykres.

W tym przypadku nie można stosować histogramu, należy zastosować wykres powierzchniowy, np. wykres kołowy!!:




Źródło: Dane z zadania 4.

---