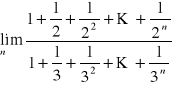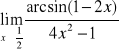Zad.1
Korzystając z definicji granicy ciągu wykazać, że
Zad.2
Obliczyć granice ciągów:
Zad.3
Wybierając odpowiednie podciągi udowodnić, że ![]()
nie istnieje.
Zad.4
Wykazać zbieżność ciągu o wyrazie ogólnym 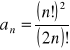
i obliczyć jego granicę.
Zad.5.
Obliczyć ![]()
, gdy ![]()
, ![]()
, …,![]()
.
Zad.6
Korzystając z definicji Heinego granicy funkcji uzasadnić, że ![]()
.
Zad.7
Wykazać, że ![]()
nie istnieje.
Zad.8
Obliczyć granice funkcji:
Zad.9
Udowodnić, że funkcja 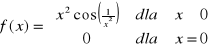
jest ciągła w ![]()
.
Zad.10
Zbadać ciągłość funkcji ![]()
.
Zad.11
Uzasadnić, że równanie ![]()
ma rozwiązanie w przedziale 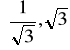
.
Wyszukiwarka
Podobne podstrony:
materiały budowlane, Budownictwo studia pł, SEMESTR I, SEMESTR I, materiały budowlane, materiały lab
analiza1, Budownictwo studia pł, SEMESTR I, SEMESTR I, matematyka, Analiza matematyczna
Materialy budowlane asfalt, Budownictwo studia pł, SEMESTR I, SEMESTR I, materiały budowlane, materi
dyskretna-przyklad-zadania-na-pierwsze-kolokwium, Studia, PWR, 2 semestr, Matematyka dyskretna, kolo
zadania z egzaminu termin II, Studia, ZiIP, SEMESTR III, Matematyka
Sprawozdanie nr 1 CECHY TECHNICZNE MATERIAfLOW BUDOWLANYCH, Budownictwo studia pł, sprawka maater
fizyka - sprawko t1a, Budownictwo studia pł, Fizyka-sprawozdanie
sprawouuzdanie uunr 1.x, Budownictwo studia pł, sprawka maateriały budowlane
matematyka, STUDIA, Polibuda - semestr I, Matematyka, Matematyka, Ściągi
sprawozdanie e6, Budownictwo studia pł, Fizyka-sprawozdanie
twierdzenie rolla, STUDIA, Polibuda - semestr I, Matematyka
GEOMETRIA ANALITYCZNA, STUDIA, Polibuda - semestr I, Matematyka, Matematyka, Ściągi
dyskretna2, Studia, PWR, 2 semestr, Matematyka dyskretna
dyskretna-egzamin-zaoczne-szablon, Studia, PWR, 2 semestr, Matematyka dyskretna, kolokwium
więcej podobnych podstron