Mariola Wiśniewska

Zbigniew Zaleski

GiSzN Grupa 3 para nr 9

Sprawozdanie nr 4

Ćwiczenie nr 10: Wyznaczanie modułu sztywności metodą dynamiczną.

1.Pojęcia związane z tematem:

Moduł sztywności- Moduł Kirchhoffa inaczej moduł odkształcalności postaciowej albo moduł sprężystości poprzecznej. Współczynnik uzależniający odkształcenie postaciowe materiału od naprężenia, jakie w nim występuje. Jednostką modułu Kirchhoffa jest pascal. Jest to wielkość określa

Sens fizyczny modułu sztywności G

G = τ, gdy tgγ=1. Moduł sztywności G liczbowo jest równy naprężeniu stycznemu τ, gdy ciało zostanie odkształcone o taki kąt γ, którego tangens jest równy jedności. Jest to kąt 45˚. Tak duże odkształcenia (sprężyste) są w praktyce na ogół nieosiągalne, jednakże powyższa interpretacja stałej G nie jest przez to podważona. Podobnie ze wzoru
wynika że G = τ gdy tgγ=1 ( jeden radian).

Jednostką G jest
. Wartości modułów sprężystości postaciowej G podają tablice fizyczne, np. moduł sztywności stali strunowej jest rzędu 10¹¹ Pa.

Czyste odkształcenie postaci obserwuje się podczas skręcania np. drutu lub pręta o kształcie walca, którego górny koniec jest umocowany, a na dolny działa siła styczna, powodująca jego skręcenie o kąt ∆φ. W tym przypadku każdy element objętości ciała równoległy do osi skręcania doznaje ścięcia lub skręcenia prostego.

Sztywność- zdolność ciała do przeciwstawiania się odkształceniu. Sztywność charakteryzuje w większości odkształceń moduł Younga.

Moduł Younga charakteryzuje twardość materiału (rozumianą jako oporność na odkształcenia sprężyste, a nie na rozbicie czy rozerwanie).

Znajomość modułu dla danego materiału pozwala obliczyć przyrost długości i prętów lub drutów, wywołany działaniem siły normalnej F:

stąd:
S - przekrój poprzeczny

Z wzorów tych wynika, że jeżeli ∆l = l₀ to
lub E=p tzn. ze moduł Younga liczbowo jest równy takiemu naprężeniu zewnętrznemu p, które spowodowałoby wydłużenie drutu ∆l równe długości początkowej (czyli drut miałby podwójną długość).

Moduł Younga podaje się w paskalach (Pa),

Naprężenie, miara sił wewnętrznych powstających w ciele pod wpływem zewnętrznej, odkształcającej siły. W danym punkcie naprężanie określone jest wektorem P=dF/dS, gdzie dF/dS oznacza siłę działającą na nieskończenie mały element powierzchni przekroju ciała.

Naprężenie dzieli się na: działające w kierunku prostopadłym do powierzchni przekroju S, nazywane naprężeniem normalnym σ, oraz na działające w kierunku stycznym do powierzchni (naprężenie styczne τ), przy czym zachodzi równość P²=σ²+τ².

Odkształcenie postaciowe- zmiana wzajemnych odległości pomiędzy punktami ciała, powstająca w wyniku naprężeń spowodowanych przez rozciąganie, ściskanie, zginanie lub skręcanie. Wyróżniamy odkształcenia plastyczne i sprężyste.

Odkształcenie plastyczne, odkształcenie trwałe, nie zanikające po usunięciu obciążeń (obciążenie), które je wywołały. Odkształcenie plastyczne może powstać przez poślizg - przesunięcie jednej części kryształu względem drugiej lub poprzez bliźniakowanie - obrót jednej części kryształu względem drugiej w taki sposób, że obie części kryształu przyjmują symetryczne położenie.

Odkształceniem sprężystym nazywamy takie odkształcenie, które ustępuje po usunięciu siły, która je spowodowała. Odkształcenia sprężyste występują w każdej konstrukcji budowlanej, maszynie, urządzeniu. Najczęściej spotykanymi odkształceniami są: rozciąganie, ściskanie, skręcanie. Reakcją na rozciąganie jest przyciąganie się cząsteczek, zaś na ściskanie odpychanie się. Odkształcenia sprężyste nie występuje w ciałach idealnie plastycznych

Rozciąganie- oddziaływanie dwóch przeciwnie skierowanych współliniowych sił.

Ściskanie, rodzaj obciążenia ciała (elementu konstrukcyjnego), na które składają się dwie przeciwnie działające siły F, powodujące ściśnięcie ciała w kierunku linii działania tych sił (naprężenia normalne panujące w przekroju poprzecznym ciała określone są zależnością: δ=F/S, sprężyste zaś skrócenie - ściśnięcie ciała: Δl=Fl/(ES), gdzie: δ - naprężenie, F - siła działająca na ciało, S - pole przekroju poprzecznego, Δl - skrócenie ciała, l - długość początkowa, E - współczynnik sprężystości wzdłużnej - tzw. moduł Younga).

Próba wytrzymałościowa na ściskanie jest podstawową próbą w badaniach wytrzymałościowych materiałów. Polega na określaniu granicznych wartości sił ściskających, powodujących zniszczenie elementu lub trwałe odkształcenie, które uniemożliwia dalsze jego użytkowanie.

Skręcanie- rodzaj naprężenia i towarzyszącego mu odkształcenia, powstającego przy działaniu pary sił o wektorach prostopadłych do rozpatrywanego przekroju, tworzących moment skręcający.

Bezwładność - właściwość wszystkich ciał materialnych, polegająca na tym, że w inercjalnym układzie odniesienia, jeśli na ciało nie działa siła lub działające siły równoważą się, to porusza się ono ruchem jednostajnym lub spoczywa. Zmiana prędkości ciała wymaga działania siły. Bezwładność ciał postulowana jest przez zasady dynamiki Newtona. Miarą bezwładności ciała jest jego masa, natomiast jej odpowiednikiem w ruchu obrotowym - moment bezwładności

Moment bezwładności to miara bezwładności ciała w ruchu obrotowym względem określonej, ustalonej osi obrotu. Im większy moment, tym trudniej zmienić ruch obrotowy ciała, np. rozkręcić dane ciało lub zmniejszyć jego prędkość obrotową.Nieznane są ani źródła jej pochodzenia ani mechanizmy jej powstawania, większość fizyków przyjmuje bezwładność jako cechę materii.

Prawo Hooke'a - prawo mechaniki określające zależność odkształcenia od naprężenia. Głosi ono, że odkształcenie ciała pod wpływem działającej nań siły jest wprost proporcjonalne do tej siły.

Ciśnienie statyczne - jest to jednostkowa siła powierzchniowa, z jaką działają na siebie dwa stykające się elementy przepływającego lub będącego w spoczynku płynu, które znajdują się w danej chwili w rozpatrywanym punkcie przestrzeni.

Wyprowadzenie wzorów roboczych. Gdy odkształcenie jest sprężyste, ciało będzie wykonywało drgania obrotowe o okresie:

gdzie:

I - moment bezwładności ciała

D - moment kierujący

Moment kierując D zależny jest od modułu sztywności G i geometrycznych wymiarów ciała:

Ostatecznie otrzymujemy:

Korzystając z powyższego wzoru wyznaczymy moment sztywności G, który jest związany bezpośrednio z okresem drgań T. Wcześniej należy jeszcze wyliczyć moment bezwładności I. W tym celu przeprowadzamy doświadczenie ze wspomnianym wcześniej wahadłem torsyjnym. Drut mocujemy jednym końcem w uchwycie A natomiast drugi koniec w uchwycie krzyżaka B. Skręcając o pewien kąt krzyżak, w wyniku siły sprężystości drutu krzyżak będzie wykonywał drgania w płaszczyźnie poziomej. Mierzymy okresy drgań dla dwóch różnych momentów bezwładności krzyżaka. W tym celu stosujemy cztery ciężarki o jednakowych masach. Umieszczamy je w odległości d₁ od osi obrotu krzyżaka i dokonujemy pomiaru okresu T₁. Potem umieszczamy ciężarki w odległości d₂ i mierzymy okres T₂.

gdzie I_k to moment bezwładności krzyżaka

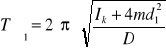
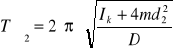
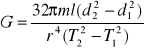
Opis wykonania zadania:

1. Wyznaczyć masy ciężarków i umieścić je na krzyżaku K w odległości d^.

2. Wprawić krzyżak w drgania „skrętne" i stoperem zmierzyć czas 20 okresów. Pomiar wykonać 3 razy i obliczyć średnią wartość okresu T_1ŚT.

3. Zmienić położenie ciężarków (na odległość d₂) i zmierzyć okres T_2śr jak wyżej.

4. Zmierzyć długość drutu miarką milimetrową oraz jego średnicę śrubą mikrometryczną.

5. Dane podstawić do wzoru
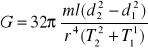
   obliczyć moduł sztywności.

6. Wyniki umieścić w wyżej zamieszczonej tabelce.

T1 [s]	T1śr [s]	T2 [s]	T2śr [s]	m [kg]	l [m]	r [m]	G [N/m^2]

---