Egzamin z matematyki dyskretnej 14 września 2011

Imię:

Nazwisko:

Grupa:

Numer Indeksu:

Uwagi:

1. Czas rozwiązywania 100 minut.

2. Ewentualne wątpliwości związane z niejednoznacznością sformułowań w zadaniach należy umieścić obok udzielonych odpowiedzi.

3. Dozwolone jest korzystanie z pomocy wyłącznie w formie własnoręcznych notatek. Nie wolno korzystać z książek i urządzeń elektronicznych.

4. W trakcie egzaminu nie wolno opuszczać sali przed oddaniem pracy.

Zad. 1. (9 pkt.) Wyraź równoważność za pomocą wyłącznie koniunkcji i negacji:

p ↔ q ⇔ ~ (p ∧ ~q) ∧ ~ (~p ∧ q)

Zad. 2 (8 pkt.) Wyznacz moce zbiorów, gdzie A = {1,2, 3, {1, 2, 3}}, B = {{1,2},1,2}, C = {{1,2,3},1,2}

|(A \ B) × C| = _.6 |(A \ C) × (B \ A)| = 1

|(A × C) \ (B × A)| = _.6 |(A ∪ B) \ C| = 2

Zad. 3. (9 pkt.) Uniwersum jest zbiorem studentów. Definiujemy następujące predykaty: L(x, y) - y jest lubiany przez x; M(x) - x lubi matematykę; R(x, y) ⇔ x = y

Wyraź w języku rachunku predykatów pierwszego rzędu, korzystając wyłącznie ze zdefiniowanych powyżej predykatów, następujące zdania: (a) Tylko jeden student lubi matematykę. (b) Wszyscy lubią studentów, którzy lubią matematykę. (c) Pewien student jest nielubiany przez wszystkich.

(a) _.∃_x[M(x) ∧ ∀_y(M(y) → R(x, y))]

(b) ∀_x[M(x) → ∀_y(L(y, x))]_.

(c) _. ∃_x[∀_y(~ L(y, x))]

Zad. 4. (8 pkt.) Niech R(A) oznacza liczbę relacji symetrycznych w zbiorze A. Wyznacz:

R({1, 2}) = 2³ R({1, 2, 3}) = 2⁶

R({1, 2, 3, 4}) = _. 2¹⁰ R({1, 2, 3, 4, 5}) = 2¹⁵

Zad. 5. (9 pkt.). Przedstaw przykład relacji równoważności w zbiorze liczb naturalnych, która ma dokładnie dwie klasy abstrakcji - jedną skończoną i jedną nieskończoną.

xRy ⇔ ( x = 1 ∧ y = 1) ∨ ( x > 1 ∧ y > 1)

Zad. 6. (9 pkt.) Na ile sposobów można ułożyć 10-cio literowe słowo z liter {a, b, c, d, e} aby

(a) każda litera wystąpiła dokładnie dwa razy _.10! / 2⁵

(b) każda litera wystąpiła co najmniej raz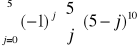

(c) litera „a” wystąpiła dokładnie 5 razy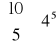

Zad. 7 (6 pkt.) Wyznacz odpowiednie parametry zadanych grafów:

	Liczba chromatyczna	Długość najdłużeszego cyklu	Długość najkrótszego cyklu
K7 - e	6	7	3
K3,5,10	3	16	3
W6	4	6	3
C7 + C4	5	11	3

Zad. 8 (8 pkt.) Udowodnij, że dla każdej liczby naturalnej n zachodzi: 9 | 4ⁿ + 6n - 10. Dowód przedstaw na odwrocie kartki.

(1) Definiujemy P(n) ⇔ 9 | 4ⁿ + 6n - 10

(2) 9 | 0 ⇒ P(1)

(3) P(n) ⇒ 9 | 4ⁿ + 6n - 10 ⇒ 9 | 4(4ⁿ + 6n - 10) ⇒ 9 | 4(4ⁿ + 6n - 10) - 9(2n - 4) ⇒ 9 | 4ⁿ⁺¹ + 6n - 4 ⇒ 9 | 4ⁿ⁺¹ + 6(n + 1) - 10 ⇒ P(n + 1)

Na mocy indukcji mamy ∀_n(P(n))

---