Grupa laboratoryjna: 204 Nr ćwiczenia: 56

W skład grupy wchodzą:

Temat ćwiczenia:

Badanie wpływu temperatury na przewodnictwo elektryczne ciał stałych.

Wydział: Ochrona Środowiska

Semestr: Drugi

Studia: Dzienne-Inżynieskie

Na podstawie doświadczeń stwierdzono, że natężenie prądu I przepływającego przez przewodnik jest wprost proporcjonalne do napięcia U na końcach przewodnika oraz odwrotnie proporcjonalne do oporności przewodnika. Jest to prawo Ohma.

Istotę oporu elektrycznego w przewodnikach wyjaśnia się na gruncie elektronowej teorii budowy materii. Prąd elektryczny płynący w przewodniku w postaci strumienia elektronów napotyka na opór elektryczny. Powodem tego są zderzenia płynących elektronów z dodatnimi jonami metalu, tworzącymi sieć krystaliczną, w wyniku czego elektrony tracą część energii kinetycznej. Wartość oporu przewodnika jest tym większa, im jest dłuższy przewodnik oraz im mniejszy jest jego przekrój. Liczba zderzeń jest tym większa, im więcej swobodnych elektronów wypełnia przestrzeń oraz im większe są wychylenia jonów z położenia równowagi. Amplituda drgań jest uzależniona od temperatury. Wynika stąd, że opór elektryczny wzrasta wraz ze wzrostem temperatury. Dla metali w niezbyt szerokim paśmie temperatur (243K-423K) zależność oporu od temperatury wyraża się wzorem:

Rt=R0(1+T)

R0 - opór elektryczny w temperaturze otoczenia,

T - przyrost temperatury,

- Temperaturowy współczynnik oporności elektrycznej.

Wykresem zależności oporu metali od temperatury jest linia prosta nachylona pod kątem ostrym do osi temperatury co pokazane jest na powyższym wykresie.

Z powyższej zależności wynika, że w temperaturach bliskich zera bezwzględnego opór przewodników maleje do wartości bliskiej zera. Taką właściwość niektórych metali nazywa się nadprzewodnictwem.

Zależność oporu elektrycznego nadprzewodników od temperatury przedstawia wykres zamieszczony obok. Dla bardzo niskich temperatur obszar nadprzewodnictwa zaznaczony jest odcinkiem OM.

Do metali nadprzewodzących zalicza się między innymi ołów, glin, cynk, niob, hafn.

Istnieje jeszcze inna grupa ciał stałych, która wykazuje przewodnictwo w określonych warunkach. Wyjaśnienie przewodnictwa tych ciał opiera się na fizyce kwantowej. Jak wiadomo, struktura większości ciał stałych charakteryzuje się krystaliczną budową. Z powodu bliskiego sąsiedztwa atomów w sieci krystalicznej na elektrony działają siły przyciągania nie tylko własnych jąder lecz także i sąsiednich. W wyniku tych oddziaływań powstają nowe, dozwolone poziomy energetyczne, tworzące odpowiednio szerokie pasma energetyczne. Pasma energetyczne kolejnych warstw powłoki elektronowej są tym szersze im większa jest ich odległość od jądra. Są one też oddzielone od siebie pasmami energii wzbronionej dla elektronów. Zewnętrzne pasmo energetyczne nazywane jest pasmem przewodnictwa.

Jeżeli pasmo walencyjne jest zapełnione w całości, a pasmo przewodnictwa jest puste i jeżeli są one oddzielone odpowiednio szerokim pasmem energii wzbronionej to niemożliwe jest przewodzenie prądu i takie ciała nazywane są izolatorami. Pomiędzy przewodnikami, a izolatorami znajduje się grupa ciał nazywana półprzewodnikami. Aby półprzewodnik mógł przewodzić prąd należy przenieść część elektronów z pasma walencyjnego do pasma przewodnictwa. Proces ten jest możliwy przez ogrzanie ciała, wprowadzenie do niego domieszek czy oświetlanie światłem o odpowiedniej częstości.

Tak więc wraz ze wzrostem temperatury przewodnictwo wzrasta, czyli opór maleje ekspotencjalnie, co pokazuje zależność:

E - szerokość pasma wzbronionego,

k - stała Boltzmana

Rpo -stała oporności zależna od koncentracji nośników ładunku w stanie podstawowym i ich ruchliwości.

W temperaturze zera bezwzględnego półprzewodnik jest w stanie podstawowym, tzn. ma całkowicie zapełnione pasmo walencyjne, a pasmo przewodnictwa jest puste. Tak więc, przewodnictwo może zachodzić poprzez przeniesienie elektronów z pasma zapełnionego do pustego w wyniku podwyższenia jego temperatury.

Logarytmując powyższe równanie otrzymamy liniową zależność lnR od odwrotności temperatury w skali bezwzględnej 1/T:

Wyznaczając parametry prostej korelacji (y=ax+b) dopasowanej do eksperymentalnego wykresu funkcji

R/Ro=f(T) - dla przewodnika - otrzymamy temperaturowy współczynnika oporności, który stanowi współczynnik kierunkowy tej prostej,

lnR=f(1/T) - dla półprzewodnika - szerokość pasma wzbronionego E dla badanego półprzewodnika obliczyć można z wartości współczynnika kierunkowego prostej. Jego wartość jest równa E/k. Wyraz stały prostej korelacji jest równy Rpo.

Przebieg doświadczenia.

1. Odczytujemy temperaturę początkową To oraz mierzymy wartości oporności początkowych Ro badanych elementów.

2. Następnie włączamy grzałkę. czekamy aż temperatura wzrośnie o 10 stopni. Odczytujemy wartość temperatury i oporności. Powtarzamy cykl grzania i pomiarów do osiągnięcia temperatury oleju o wartości 70 - 80 C.

3. Odczytane wartości umieszczamy w tabeli 1, wraz z błędami bezwzględnymi pomiaru wartości oporności i wartościami ilorazu R/Ro dla przewodnika oraz wartościami odwrotności temperatury w skali bezwzględnej.

4. Sporządzamy wykresy

a) R/Ro=f(T) - dla przewodnika

b) lnR=f(1/T) - dla półprzewodnika

c) R=f(T) - dla półprzewodnika.

5. Obliczamy parametry prostych korelacji i przedstawiamy w tabeli 2. Na wykresie c wykreślamy krzywą R=Ro exp(E/kT).

Tabela 1.

	przewodni	k				półprzewo	dnik
t [C]	T [K]	R []	R []]	R/Ro	T [K]	1/T [K ]	R [k]	R [k]
21		17.1			294	0.0034	10
30	9	17.4	0.3	1.017	303	0.0033	7.2	2.8
40	19	18	0.9	1.052	313	0.0032	5.1	4.9
50	29	18.8	1.7	1.099	323	0.0031	3.1	6.9
60	39	19.5	2.4	1.14	333	0.003	2.2	7.8
70	49	20.4	3.3	1.192	343	0.0029	1.5	8.5
80	59	21	3.9	1.228	353	0.0028	1.1	8.9

Temperatura początkowa To wynosi 21C, a opór początkowy Ro wynosi 17.1 dla przewodnika oraz

10 k dla półprzewodnika.

Temperatura bezwzględna w stopniach Kelvina T=273.15+t(C).

Przyrosty oporności wynoszą

dla przewodnika

dla półprzewodnika

Wykres 1 - R/Ro=f(T) - dla przewodnika

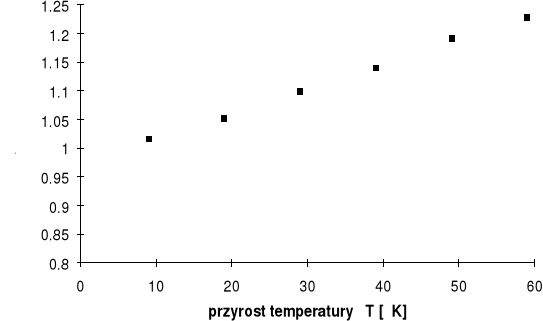
Wykres 2 - lnR=f(1/T) - dla półprzewodnika

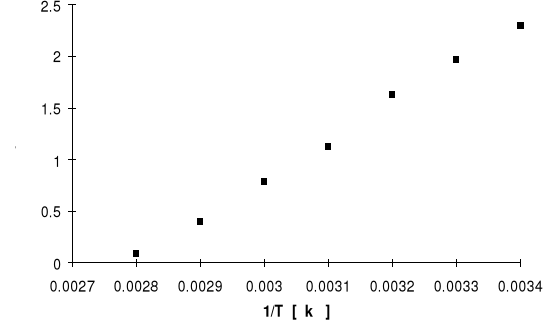
Wykres 3 - R=f(T) - dla półprzewodnika

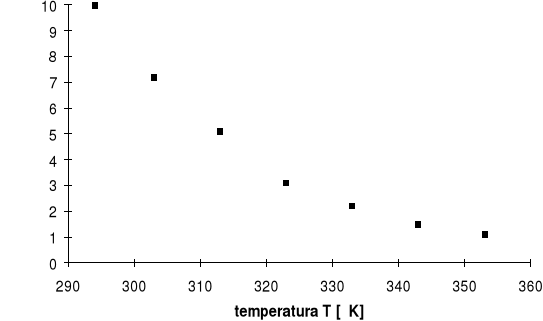
Z wykresu R/Ro=f(T) odczytujemy współczynnik kierunkowy prostej a=0.004058, który równy jest

termicznemu współczynnikowi oporności.

Z wykresu lnR=f(1/T) odczytujemy współczynnik kierunkowy a=3973.73, który odpowiada ilorazowi

E/k i stąd obliczamy szerokość pasma wzbronionego E=a k. Wyraz stały b=-4.24 jest równy lnRpo i stąd

obliczamy Rpo=e .

E=3973.731.380610 =5.48610 J/K

1eV=1.602210 J , stąd E=5.48610 /1.602210 =0.342eV

k

Wszystkie wyniki zapisujemy w tabeli 2 i stanowią one ostateczny wynik doświadczenia, z którego

wynika,że wraz ze wzrostem temperatury przewodnictwo elektryczne maleje w przewodnikach

natomiast w półprzewodnikach rośnie.

Tabela 2.

przewodnik		pół	przewodn	ik
R/Ro	[K ]	Rpo [k]	E/k [K]	E [eV]
1.121	0.004058	0.0144	3973.73	0.342

Badanie wpływu temperatury na przewodnictwo elektryczne ciał stałych

4

---