Marcin Malczewski

Sławomir Mrozik

gr. lab. 212

INFORMATYKA

Ćwiczenie nr 61

WYZNACZANIE ROZKŁADU POTENCJAŁU POLA ELEKTRYCZNEGO METODĄ SONDY PŁOMYKOWEJ

1. Część teoretyczna.

Natężenie pola elektrostatycznego E - wielkość wektorowa opisująca pole definiowane w danym punkcie jako stosunek siły F działającej na umieszczony w tym punkcie spoczywający próbny ładunek (dodatni) +q do wartości tego ładunku.

Kierunek i zwrot wektora E jest taki sam jak kierunek i zwrot siły działającej na dodatni ładunek próbny.

Potencjał pola elektromagnetycznego V definiujemy w danym punkcie pola jako stosunek energii potencjalnej Ep punktowego ładunku q umieszczonego w tym punkcie do tego ładunku.

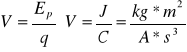
Napięcie elektryczne, U - różnica potencjałów V między dwoma punktami pola elektrycznego. Związek między wartością natężenia pola E a spadkiem potencjału V. Wartość natężenia pola elektrostatycznego E jest równa stosunkowi spadku potencjału V na niewielkim odcinku prostopadłym do powierzchni ekwipotencjonalnej (potencjał ma stałą wartość) do długości L tego odcinka.

Znak "-" wynika stąd, że zwrot wektora E jest przeciwny do spadku potencjału.

2. Część doświadczalna.

W celu dokonania pomiaru wykonujemy następujące czynności:

1. Sprawdzić czy zasilacz WN jest odłączony od sieci .

2. Ustawiamy płytki kondensatora równolegle względem siebie na odległość d = 40 mm .

3. Zapalamy sondę płomykową ( ustawiamy jak najmniejszy płomień ) .

4. Zasunąć przednią szybę.

5. Włączamy zasilacz woltomierza i zasilacz wysokiego napięcia.

6. Przesuwamy sondę do położenia przy którym wskazanie woltomierza wynosi około 600 V.

7. Przesuwamy sondę w kierunku prawej płytki co 3 mm i wykonujemy pomiar potencjału w kolejnych 9 punktach.

8. Wyłączyć zasilacz WN i rozsunąć okładki na odległość d₂ = 80 mm.

9. Powtórzyć czynności jak w punktach 5 - 7, ale pomiary wykonywać co 5 mm.

10. Wyłączyć zasilacz wysokiego i rozsunąć okładki na odległość d₃ = 120 mm.

11. Powtórzyć czynności jak w punktach 5 - 7, ale pomiary wykonywać co 5 mm.

Wyniki pomiarów zestawiamy w tabeli:

D1=40 mm		d2=80 mm		d3=120 mm
U	l	U	l	u	l
V	mm	V	mm	V	mm
600	10	600	21	600	38
880	13	760	26	700	43
1160	16	960	31	780	48
1400	19	1140	36	900	53
1680	22	1340	41	1020	58
1960	25	1560	46	1140	63
2200	28	1780	51	1280	68
2470	31	2000	56	1440	73
2720	34	2220	61	1560	78
		2460	66	1720	83
				2680	71	1890	88
				2920	76	2080	93
						2260	98
								2440	103

Korzystając z tablicy danych:

x	y	x*y	x
10	600	6000	100
13	880	11440	169
16	1160	18560	256
19	1400	26600	361
22	1680	36960	484
25	1960	49000	625
28	2200	61600	784
31	2470	76570	961
34	2720	92480	1156
198	15070	379210	4896

oraz używając wzorów:

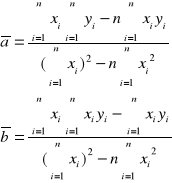
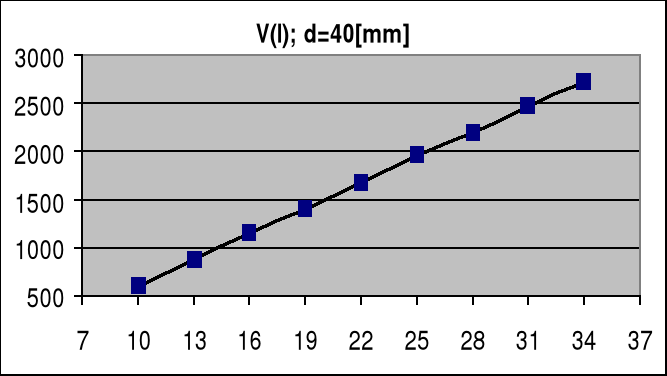
obliczyliśmy a₁, b₁(dla d=40):

a₁=88,3 [V /mm]

b₁=-267,7 [V]

oraz uzyskaliśmy wykres:

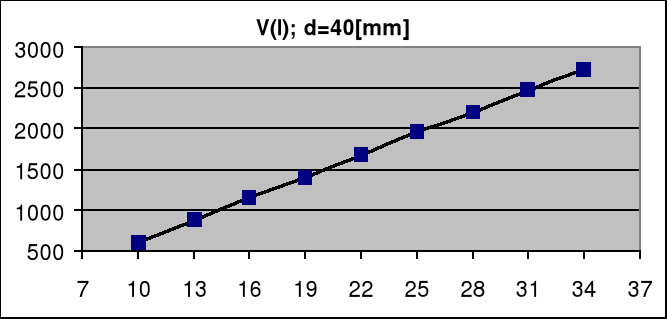
Używając komputera, wyznaczyliśmy współczynniki a₂, b₂ (d=80), a₃, b₃ (d=120) oraz otrzymaliśmy dwa wykresy przedstawiające zależność f(l) = U kolejno dla :

a₂ =42,1 [V /mm]

a₂=0,6 [V /mm]

b₂ =-344,4 [V]

b₂ =33,5 [V]

a₃=28,4 [V /mm]

a₃=0,9 [V /mm]

b₃ =-587,8 [V]

b₃ =65,1 [V]

Obliczanie teoretycznych wartości natężenia pola elektrycznego ( Et ) (dla poszczególnych wartości d i zadanego napięcia między okładkami) oraz względnego odchylenia ( wartości doświadczalnych natężenia pola elektrycznego ( Ed ) od wartości teoretycznych ( Et )

Teoretyczną wartość natężenia pola elektrycznego obliczamy korzystając ze wzoru Et = U / d [ v / m. ]. Obliczamy wartość ΔE wiedząc, że ΔE = Ed - Et ( wartość Ed jest równa współczynnikowi kierunkowemu a ). Wartość błędu obliczamy ze wzoru :

δ=|ΔE|/Et*100%.

d1=40 mm			d2=80 mm			d3=120 mm
Ed [V/mm]	Et [V/mm]	δ [%]	Ed [V/mm]	Et [V/mm]	δ [%]	Ed [V/mm]	Et [V/mm]	δ [%]
88,3	75,0	18	42,1	39,0	7	28,4	26,0	9

---