Grupa laboratoryjna: 204 Nr ćwiczenia: 13

W skład grupy wchodzą:

Temat ćwiczenia:

Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego (Katera)

Wydział: Ochrona Środowiska

Semestr: Drugi

Studia: Dzienne-Inżynieskie

Potencjał pola grawitacyjnego:

Skalarna lub wektorowa funkcja reprezentująca mierzalne pole wektorowe. Pole to otrzymuje się przez obliczając gradient pola skalarnego lub rotacje pola wektorowego. Jedno pole może być opisywane przez kilka funkcji pola różniących się stała dla pola skalarnego lub gradientem dowolnej funkcji skalarnej - dla pola wektorowego. Jest to związane z faktem, ze przy różniczkowaniu tych wielkości wszystkie składowe wektora będącego wynikiem różniczkowania są równe 0.

grad C= [0,0,0]

rot grad(x,y,z)=[0,0,0]

fi= -(GMm/r) ; F= -grad fi

gdzie: G - stała grawitacji, M,m - przyciągające się masy, r - odległość miedzy ich środkami

F - siła przyciągania.

W tym przypadku potencjał jest energia potencjalna. W odniesieniu do ciął w pobliżu pow. Ziemi energie potencjalna cechuje się zwykle inaczej.

fi= -(G Mz m/ Rz + x)=- m g Rz + m g x

gdzie: Mz, Rz - masa i promień Ziemi, x - odleg. od powierzchni Ziemi,

g= (GMz/Rz^2) - przyspieszenie ziemskie, a stała C wybiera się tak, by

fi= mgx

Czasem definiuje się również potencjał:

fi= -(GM/ r) ; E= - grad fi

Oddziaływania grawitacyjne - jest to jedno z czterech podstawowych oddziaływań występujących w przyrodzie . Oddziaływanie grawitacyjne jest odpowiedzialne za występowanie zjawisk przyciągania grawitacyjnego. Charakterystyczna cecha odróżniająca oddziaływania grawitacyjne od innych oddziaływań jest to, ze siła działająca na ciała umieszczone w polu grawitacyjnym jest ściśle proporcjonalna do masy bezwładnej ciała. W rezultacie ruch ciała w polu grawit. nie zależy od jego natury, co po raz pierwszy sprawdził Galileusz.

Moment siły - M - wielkość fizyczna wektorowa równa iloczynowi wektorowemu wektora położenia r punktu, w którym jest zaczepiona siła F, i tej siły M=r
F

Moment siły jest wektorem prostopadłym zarówno do r, jak i do F. Wartość momentu siły jest równa iloczynowi siły i jej ramienia, składowej wektora r prostopadłej do siły F, M=F*d, przy czym ramie siły d=s sin
, gdzie
- kat między wektorami r i F

Wahadłem fizycznym nazywamy bryłę sztywną, mogącą się obracać wokół poziomej osi, nie przechodzącej przez jej środek ciężkości.

Wypadkowa sił ciężkości elementów wahadła jest równa ciężarowi P=mg i jest ona przyłożona do środka ciężkości bryły S. Wahadło jest w równowadze, gdy środek ciężkości znajduje się w punkcie O.

Jeśli wahadło zostanie wychylone o niewielki kąt
z położenia równowagi, to ciężar P można rozłożyć na składowe F1 oraz F. Składowa F1 jest równoważona przez siłę Fz , a składowa F powoduje ruch środka ciężkości w kierunku punktu O. Z tego wynika wzór

F = -Psin
, czyli F = - mgsin
. A jeśli mamy mały kąt to sin
możemy zastąpić wartością kąta i otrzymamy :

F = - mg
.

Moment siły powodujący drgania względem osi obrotu Z, wyrażony wzorem M = Fd po podstawieniu będzie następujący: M= - mgd
. Pod wpływem tego momentu wahadło uzyska przyspieszenie kątowe
. Jest ono zależne od momentu siły M oraz momentu bezwładności I,

M = I
czyli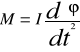
.

Podstawiając już otrzymane wzory otrzymujemy

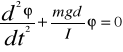
, czyli
, którą można wyrazić wzorem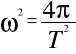

Stąd możemy obliczyć przyspieszenie ziemskie, które równe jest
.

Wahadło rewersyjne stanowi wahadło fizyczne o ustalonych osiach obrotu O1 i O2, które umieszczone są w stałej odległości od siebie (l=O1O2). Położenie masy m jest zmienne, a okres drgań wahadła wyraża się wzorem :

, gdzie I jest momentem bezwładności wahadła, a d jest odległością osi wahadła od jego środka ciężkości. Jeżeli wahadło wykonuje drgania wokół każdej z osi z jednakowym okresem, to odległość między ostrzami jest długością zredukowaną. Aby to stwierdzić, mierzy się czas t określonej ilości n wahnień, zawieszając wahadło na osi O1 przy różnych położeniach masy m. Następnie obraca się wahadło i zawiesza się je na osi O2 i powtarza czynności. Wstawiając otrzymane dane do wykresu otrzymany krzywą przecinającą się w punkcie D. Jeżeli masa m znajduje się w położeniu punktu D, oznacza to że czasy n wahnień względem obu ostrzy są sobie równe, a co za tym idzie okresy drgań są sobie równe. Wynika stąd, że l=O1O2 jest długością zredukowaną wahadła. Znając długość zredukowaną wahadła
można korzystać ze wzoru na okres wahadła matematycznego

Przebieg ćwiczenia.

1. Zostaje zmierzona odległość pomiędzy osiami wahadła (l=O1O2) i oszacowany błąd
l.

2. Wahadło zostaje zawieszone na ostrzu O1, a środek masy zostaje umieszczony na środku pręta.

3. Wykonano serię 10-ciu pomiarów czasu t dziesięciu drgań (n=10) bez zmiany punktu położenia masy. Wyniki zanotowano w tabeli 1 i obliczono z nich wartość średnią t, średni błąd kwadratowy pojedynczego pomiaru St' oraz błąd skorygowany przez współczynnik Studenta Fishera St.

Tabela 1.[s]

t1	t2	t3	t4	t5	t6	t7	t8	t9	t10	t	St'	t n	St
19.93	19.89	19.79	19.55	19.85	19.84	19.92	19.70	19.96	19.72	19.81	0.04	2.262	0.09

4. Następuje seria pomiarów czasu t' 10-ciu wahnień, przy czym masa przesuwana jest od osi O1 w kierunku osi O2 o 5 cm. Wyniki zostają zanotowane w tabeli 2

5. Wahadło zostaje powieszone na drugiej osi, po czym następuje seria pomiarów czasu t" 10-ciu wahnień również przy przesuwanej masie. Wyniki zostają zanotowane w tabeli 2

Tabela 2.

kn	[cm]	0	5	10	15	20	25	30	35	40	45	50	55	60
t'	[s]	20.18	19.90	19.84	19.68	19.42	19.28	19.16	18.85	18.77	18.63	18.51	18.47	18.56
t"	[s]	20.17	20.02	19.62	19.23	19.04	18.65	18.54	18.25	17.96	17.72	17.46	17.33	17.37

kn	[cm]	65	70	75	80	85	90	95
t'	[s]	18.66	18.68	18.90	19.00	19.30	19.53	20.01
t"	[s]	17.40	17.63	18.15	18.83	19.57	19.74

6. Sporządzono wykresy t'=f(kn) i t''=f(kn) w tym samym układzie współrzędnych

7. Z wykresu tego odczytano współrzędne t'0 i t"0

8. Na podstawie uzyskanych wyników obliczono średni czas 10-ciu drgań oraz dokładność
t0, obliczono również okres drgań wahadła T0 i
t'0. Wyniki zanotowano w tabeli 3.

9. Obliczono przyspieszenie ziemskie g i błąd bezwzględny
g. Wyniki zanotowano w tabeli 3.

Tabela 3.

t'0=19.89 [s]	t"0=19.11 [s]	t0=19.5 [s]	t'0=0.39 [s]	t0=0.1 [s]
T0= 2.01 [s]	l= 1 [m]	l=0.005 [m]	g=10.38 [m/s]	g= 0.15 [m/s]

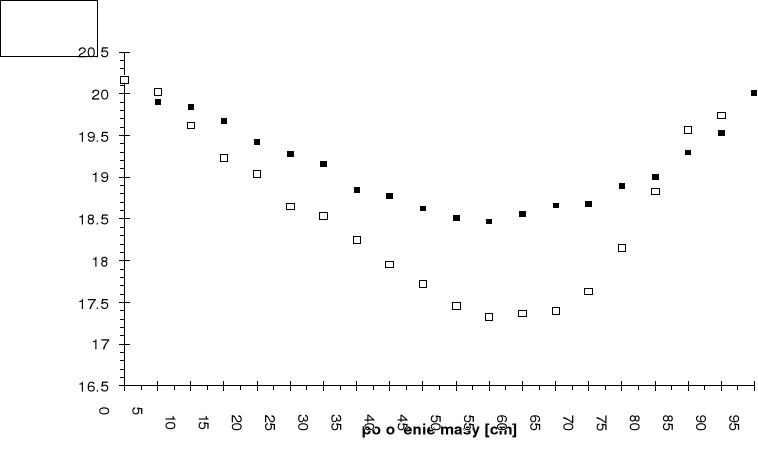
Wyznaczanie przyspieszenia ziemskiego

3

---