Robert WITEK

Grzegorz FRANEK

Łukasz POLAK

Grupa 601

ĆWICZENIE 56

Temat: Badanie wpływu temperatury na przewodnictwo elektryczne ciał stałych.

Opór elektryczny przewodników w temperaturach dużo wyższych od temperatury Debye'a rośnie liniowo wraz ze wzrostem temperatury:

(1)

gdzie: R_o - opór elektryczny przewodnika w temp. otoczenia,

ΔT - przyrost temperatury,

α - temperaturowy współczynnik oporności elektrycznej.

Dla przewodnika w tym zakresie temperatur opór elektryczny maleje eksponencjalnie ze wzrostem temperatury:

(2)

gdzie: E - szerokość pasma wzbronionego,

k - stała Boltzmana,

R_po - stała oporności zależna od koncentracji nośników ładunku
w stopniu podstawowym i ich ruchliwości.

Logarytmując obustronnie równanie (2) otrzymujemy liniowe zależności lnR od odwrotności temperatury w skali bezwzględnej 1/T [K^-1]

(3)

Wyznaczając parametry prostej korelacji y=ax+b dopasowanej do eksperymentalnego wykresu funkcji:

1. R / R_o=f (ΔT) (dla przewodnika) temperaturowy współczynnik oporności obliczyć można z wartości współczynnika kierunkowego tej prostej,

2. ln R=f (1/T) (dla półprzewodnika) szerokość pasma wzbronionego E dla badanego półprzewodnika obliczyć można z wartości współczynnika kierunkowego tej prostej. Jego wartość jest bowiem równa E/k. Wyraz stały prostej korelacji jest równy natomiast wartości ln R_po.

TABELA POMIAROWA:

	PRZEWODNIK				PÓŁPRZEWODNIK
t [^oC]	ΔT [K]	R [Ω]	ΔR	R/Ro	T[K]	1/T [K^-1]	R [kΩ]	ΔR [kΩ]
20	0	17,7	1,77	1	293,15	0,0034	11,15	1,115
30	10	18,0	1,80	1,016	303,15	0,0033	9,61	0,961
40	20	18,8	1,88	1,060	313,15	0,0032	6,46	0,646
50	30	19,7	1,97	1,093	323,15	0,0031	4,10	0,410
60	40	20,4	2,04	1,142	333,15	0,0030	2,72	0,272
70	50	21,1	2,11	1,175	343,15	0,0029	1,88	0,188
80	60	22,0	2,20	1,219	353,15	0,0028	1,36	0,136

Wykorzystując program komputerowy obliczamy współczynniki kierunkowe prostych R/R_o=f (ΔT) - dla przewodnika i lnR=f (1/T) dla półprzewodnika:

PRZEWODNIK: PÓŁPRZEWODNIK:

a= 0,005099 a= 3743,019

b= 0,981151 b= - 10,2251

Wartość pasma wzbronionego półprzewodnika obliczamy z zależności:

E=a ⋅ k

gdzie:

k - stała Boltzmana

a - współczynnik kierunkowy prostej lnR = f (1/T)

E= 3743,019 K ⋅ 8,617342⋅10^-5 eV/K = 0,32 eV

E=0,32 eV

PRZEWODNIK		PÓŁPRZEWODNIK
R/Ro	Rpo [kΩ]	Rpo [kΩ]	E/k [K]	E [eV]
1	2,667	0,036	3743,019	0,32

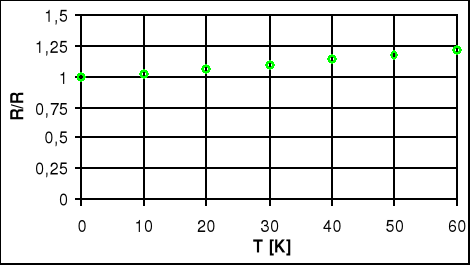
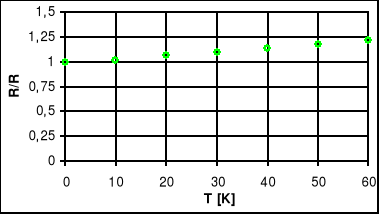
Wykres R/R_o=f(ΔT) - dla przewodnika

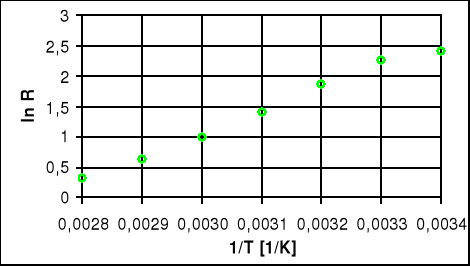
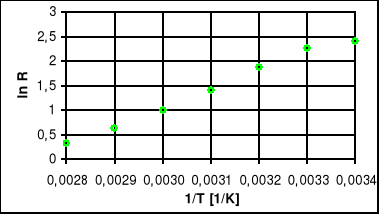
Wykres lnR=f(1/T) - dla półprzewodnika

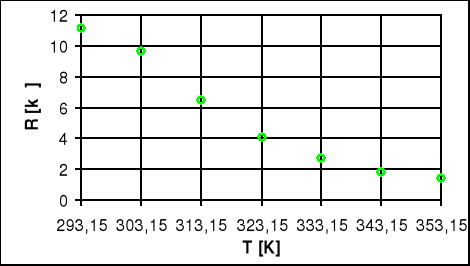
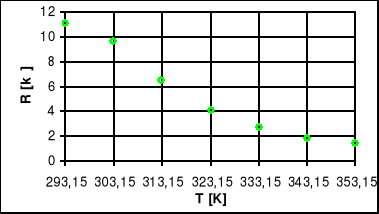
Wykres R=f(T) - dla półprzewodnika

4

ĆWICZENIE NR 56

BADANIE WPŁYWU TEMPERATURY NA PRZEWODNICTWO ELEKTRYCZNE CIAŁ STAŁYCH

---