Zad1
Opisz korelację pomiędzy zmiennymi i oszacuj współczynnik korelacji. Oszacuj wartość parametrów następującego modelu y^=b0+b1*x1. Oceń dobroć dopasowania modelu na podstawie miar S^2, SST, SSR, SSE. Wykonaj test t istotności parametru b1 dla beta1,0 i t0.975,4=2,7764
x 1 1 3 3 5 5
y 2 4 5 9 10 12
Zad2
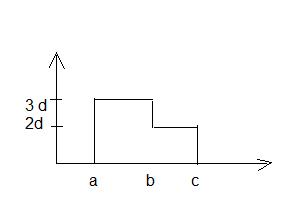
Wzrost pewnej populacji komórek można podzielić na 2 fazy widoczne pod mikroskopem. Wczesna faza rozwoju i późna faza (przed podziałem). Komórka dzieli się na 2 potomne. Na daną populację zadziałano promieniowaniem jonizującym. Wiadomo, że podana dawka promieniowania powoduje śmierć 10% komórek z pierwszej fazie i 30% komórek w późnej fazie. Czas trwania każdej z faz jest zmienną losową o rozkładzie podanym na rysunku poniżej o parametrach a=2 b=5 c=6 a druga faza o rozkładzie normalnym N(5;10). Zaproponuj model opisu dynamiki, naszkicuj schemat modelu i zbadaj jego stabilność.
Zad3
Zbadać stabilność modelu Lotki-Voltery z ograniczoną pojemnością środowiska dla ofiar. Narysować portret fazowy, narysować kilka przykładowych trajektorii, oraz zaznaczyć punkty równowagi na portrecie. Jak wpływa wprowadzenie ograniczonej pojemności środowiska na stabilność modelu porównując go do klasycznego L-V.
Wyszukiwarka
Podobne podstrony:
obrobka 2 termin, Studia, ZiIP, SEMESTR VI, Obróbka ubytkowa
Otyłość rok III semestr VI
pzs, WAT, SEMESTR VI, podstawy zabezpieczeń sieci, Egzamin
psych.mgr.1, WAT, semestr VI, Psychologia
dom0, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR VI, Woiągi
Cwiczenie 1 Zakres obliczeń modelowych 27.02.2013, Polibuda, OŚ, Semestr VI, Gospodarka odpadami
test z fizyki, Energetyka AGH, semestr 6, VI Semestr, Energia Jądrowa, EGZAMIN, EJ
karta technologiczna1, Polibuda (MiBM), Semestr VI, SKOWRON, Nowy folder, VI semestr, Talar, projekt
Pomiar i testy wpsychologii, Psychologia UŚ, Semestr VI, Diagnoza psychologiczna
fundusze strukturalne, Studia - zarządzanie zzdl, semestr VI, innowacje
2 termin-semestr zimowy, Giełdy z farmy
Zestaw A psychologia lic.zaoczne, WAT, semestr VI, Psychologia
Opis formalny-, WAT, semestr VI, Projekt zespołowy
dom1, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR VI, Woiągi
gitg-wyk3, FIR UE Katowice, SEMESTR VI, gieldy, gieldy 1, gieldy
psych.mgr2, WAT, semestr VI, Psychologia
więcej podobnych podstron