Sprawozdanie nr 1 |
Pomiar ciepła zobojętniania. Wyznaczenie stałej kalorymetru.
|
|
|
Grupa
|
Wykonali:
|
Podpis |
Ocena |
Zakres materiału teoretycznego:
zasady termodynamiki,
podstawowe funkcje termodynamiczne,
prawo Hessa,
prawo Kirchoffa,
ciepło reakcji,
ciepła przemian fazowych,
pojemność cieplna,
ciepło molowe,
ciepło właściwe,
rodzaje kalorymetrów,
metody pomiaru zmian temperatury,
ciepło neutralizacji, rozpuszczania,
ciepło molowe ciał stałych, cieczy i gazow.
Wykonanie ćwiczenia.
Przybory i odczynniki:
kalorymetr,
multimetr,
KOH w granulkach,
H2SO4 (ρ = 1,84 [g/cm3]
2 KOH + H2SO4 → K2SO4 = K2SO4 + 2 H2O
2 K+ + 2 OH - + 2 H+ + SO4-2 → 2 K+ + SO4-2 + 2 H2O
W naszym doświadczeniu:
n(KOH) = 0,5 mola,
n(H2SO4) = 0,25 mola, ,
m(KOH) = 26,05 g,
V(H2SO4) = 13,31 cm3
woda w kalorymetrze 2250 [cm3],
woda w zlewce 500 [cm3].
Pomiar zmian temperatury wykonywane w odstępach minutowych.
Wskazania multimetru przeliczono zgodnie ze wzorem:
Y = 82,034 - 53,062 log x Gdzie: x - wynik odczytu [ kΩ]
y - temperatura [C°]
Odczytane wyniki umieszczono w tabelce.
Tabela 1. Pomiar ciepła neutralizacji.
Tabela 2. Pomiar ciepła rozpuszczania.
Ciepło reakcji neutralizacji.
Ponieważ w naszym przypadku kwas, zasada, oraz sól są całkowicie zdysocjowane ciepło zobojętniania jest praktycznie równe ciepłu powstawania wody (mierzone ciepło nie zależy od rodzaju kwasu i zasady).
Biorąc pod uwagę ilość zastosowanych substancji wiemy, że w reakcji przez nas przeprowadzonej wydzieliło się 0,5 [mol] H2O.
Ciepło powstawania wody wynosi: *n = 57,36[kJ/mol]
A więc w naszym przypadku: *n = 28,68 [ kJ]
Wyznaczanie stałej kalorymetru.
*n = ΔH = (msz csz + mw cw) ΔT
*n = K. ΔT
gdzie:
K - stała kalorymetru (pojemność cieplna)
Wyznaczanie przyrostu temperatury ΔT.
TABELA 1
CZAS [min] |
OPÓR [kΩ] |
TEMPERATURA [°C] |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
|
12,91 18,89 12,86 12,85 12,82 12,81 12,73 12,50 12,38 12,27 12,20 12,13 12,07 12,03 12,00 11,96 11,93 11,91 11,89 11,87 11,85 11,84
|
23,08 23,12 23,17 23,19 23,24 23,26 23,40 23,83 24,05 24,25 24,39 24,52 24,63 24,71 24,77 24,84 24,90 24,94 24,98 25,02 25,06 25,07
|
|
metoda analityczna,
ΔT = ΔT' + Σv
gdzie:
ΔT - przyrost temperatury w całym okresie głównym trwania
ΔT' -rzeczywista różnica temperatur spowodowana tylko przebiegiem badanego procesu w okresie głównym.
Σv = vp + (z - 1) vk - suma poprawek na promieniowanie.
vp - średnia różnica temperatur pomiędzy dwoma kolejnymi punktami pomiarowymi okresu początkowego pomiaru kalorymetrycznego.
vk -dla okresu końcowego pomiaru kalorymetrycznego.
z - liczba punktów pomiarowych w okresie głównym pomiaru kalorymetrycznego.
Okres początkowy obejmował 6 pomiarów. Okres główny obejmował 10 pomiarów. okres końcowy obejmował 6 pomiarów.
Lp |
vpi [K] |
vki [K] |
1 2 3 4 5 |
0,04 0,05 0,02 0,05 0,01 |
0,03 0,04 0,04 0,04 0,01 |
vśr p = 0,034
vśr k = 0,03
Σv = vśr p + vśr k
Σv = 0,304 = 0,3 [K]
ΔT' = 1,58 [K]
Otrzymujemy:
ΔT1 = 1,88 [K]
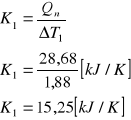
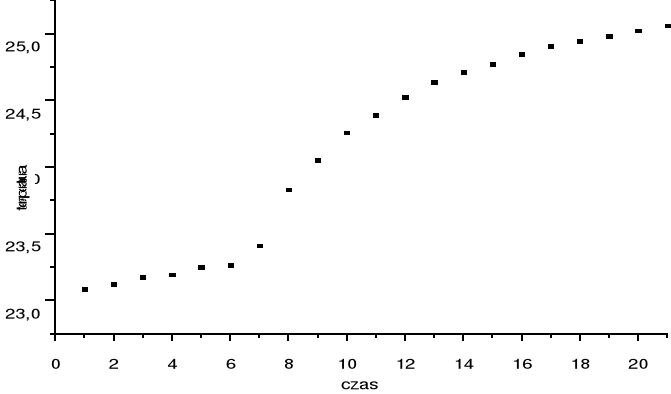
b ) metoda graficzna.
Odczytana z wykresu (metodą stycznych) wartość ΔT2 wynosi 1,35 [K]
więc
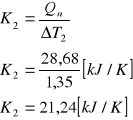
Wyznaczanie wartości średniej i błędu pomiaru.
Nr |
Ki [ kJ/K] |
Ki -Kśr |
(Ki - Kśr)2 |
1 2 |
15,25 21,24
|
-2,995 2,995 |
8,97 8,97 |
Σ=17,94
Kśr = 18,245 [kJ/K]
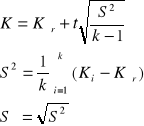
![]()
S2 = 8,97 (wariancja)
S = 2,994 (odchylenie standardowe)
Przyjęto poziom istotności pomiaru α = 0,3
liczba stopni swobody wynosi r = k - 1 = 1
Znaleziono w tablicach rozkładu t = 1,963
Błąd wynosi: ±5,877 [kJ/K]
Błąd względny: 30%
Obliczona wartość:
K = (18,245 ±5,877) [kJ/K]
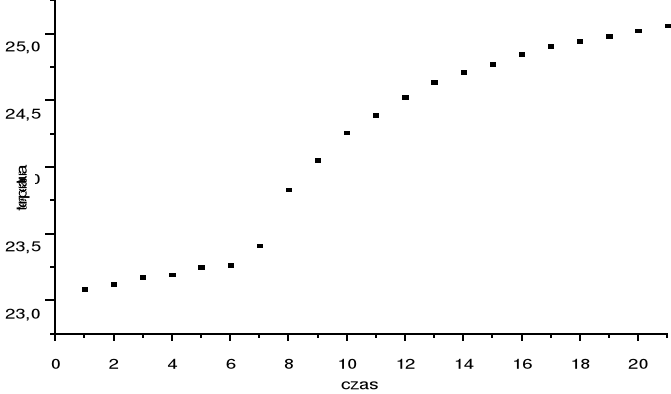
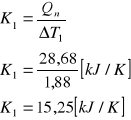
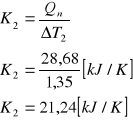
![]()
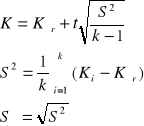
Wyszukiwarka
Podobne podstrony:
Hoffmann, W3 - chemiczny
Wilk, W3 - chemiczny
7214, W3 - chemiczny
5133, W3 - chemiczny
W3 Chemiczne skladniki komorki
Ożyhar, W3 - chemiczny
Oleksyszyn, W3 - chemiczny
Szczygieł, W3 - chemiczny
hoffmann, W3 - chemiczny
5672, W3 - chemiczny
Ożyhar, W3 - chemiczny
Lejczak, W3 - chemiczny
15, W3 - chemiczny
7386, W3 - chemiczny
(), W3 - chemiczny
(), W3 - chemiczny
Oleksyszyn, W3 - chemiczny
9451, W3 - chemiczny
ożychar, Politechnika Wrocławska, W3 - chemiczny
więcej podobnych podstron