1. Oblicz pole całkowite ostrosłupa prawidłowego czworokątnego, którego krawędź podstawy wynosi 5 cm, a długość krawędzi bocznej wynosi 7 cm.

2. Oblicz pole całkowite ostrosłupa prawidłowego pięciokątnego, jeżeli długość dłuższej przekątnej podstawy wynosi 6 cm, a wysokość ściany bocznej ma długość 8 cm.

3. Oblicz pole całkowite ostrosłupa prawidłowego czworokątnego, jeżeli przekątna podstawy ma długość 4 cm, a długość krawędzi bocznej wynosi 6 cm.

4. Oblicz wysokość ściany bocznej w ostrosłupie prawidłowym trójkątnym, którego pole całkowite wynosi 26
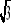
   cm², jeżeli wysokość podstawy wynosi 3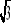
   cm.

5. Oblicz długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego, którego pole całkowite wynosi 30 cm². Wysokość ściany bocznej ma długość 4 cm.

6. Wysokość ostrosłupa prawidłowego czworokątnego ma długość 4 cm, a wysokość ściany bocznej jest nachylona do płaszczyzny podstawy pod kątem 60^o. Oblicz pole całkowite tego ostrosłupa.

7. Oblicz pole całkowite ostrosłupa prawidłowego czworokątnego, którego krawędź podstawy ma długość 6 cm, a wysokość tego ostrosłupa wynosi 4 cm.

8. Oblicz wysokość ostrosłupa prawidłowego czworokątnego, którego pole całkowite wynosi 60 cm², a przekątna podstawy ma długość 4
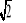
   cm.

9. Oblicz pole całkowite ostrosłupa prawidłowego trójkątnego, jeżeli krawędź podstawy ma długość 3 cm, a wysokość ściany bocznej jest nachylona do płaszczyzny podstawy pod kątem 45^o.

10. Oblicz pole całkowite ostrosłupa prawidłowego pięciokątnego o krawędzi podstawy 6 cm, jeżeli wysokość ściany bocznej jest nachylona do płaszczyzny podstawy pod kątem 30^o.

---