ZAKRES WYMAGAŃ Z MATEMATYKI

W RAMACH PRZYGOTOWAŃ

DO EGZAMINU GIMNAZJALNEGO

ZADANIA TEKSTOWE I PROBLEMY PRAKTYCZNE

TYPOWE ZADANIA Z EGZAMINÓW GIMNAZJALNYCH

Zadania praktyczne. Funkcje, wyra

ż

enia, analiza danych.

−

Prezentacja informacji za pomoc

ą

wyra

ż

e

ń

algebraicznych.

−

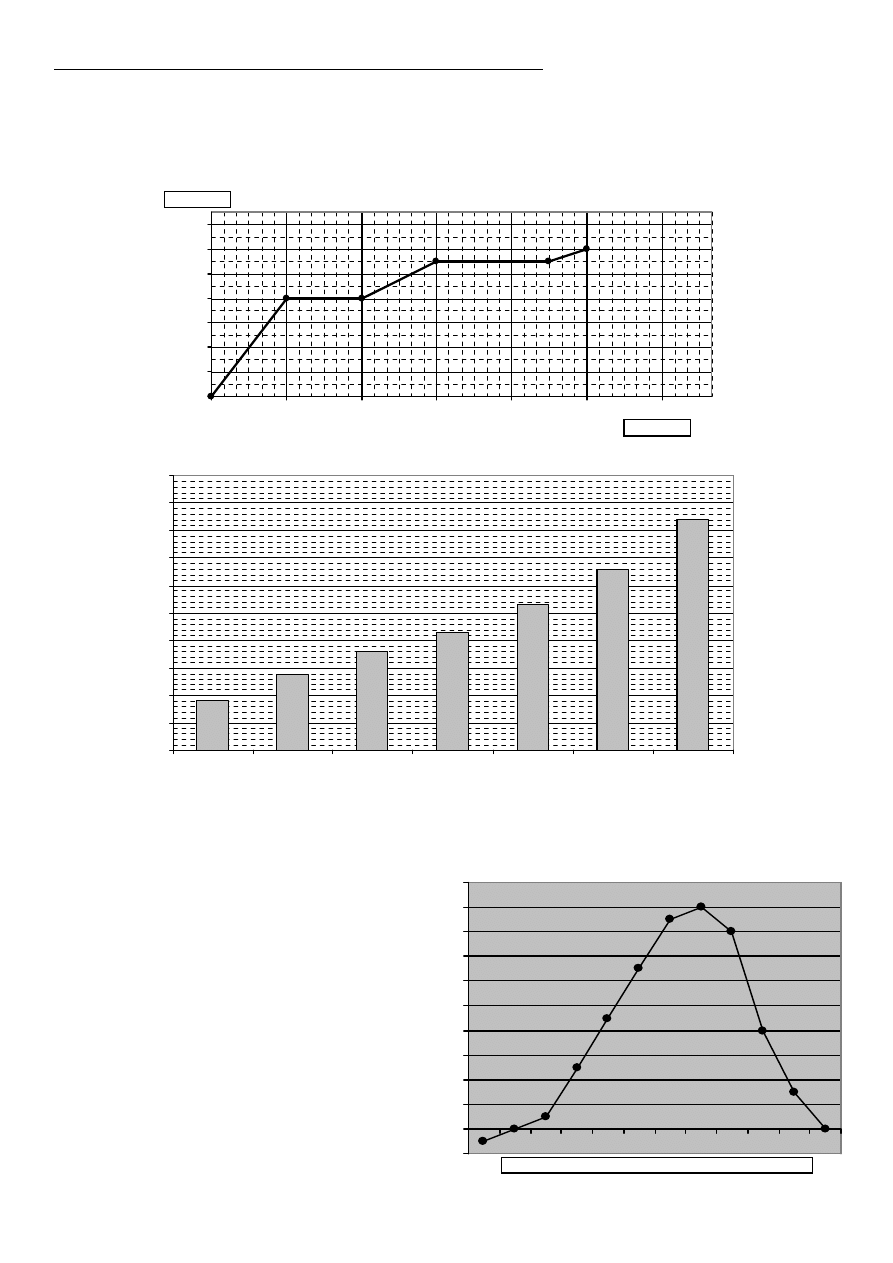
Funkcje i warto

ś

ci liczbowe wyra

ż

e

ń

.

−

Odczytywanie informacji z tabel, wykresów i diagramów.

−

Przekształcanie wzorów i matematyka w zagadnieniach fizycznych.

Zadania praktyczne. Procenty.

−

St

ęż

enia procentowe roztworów, zawarto

ść

procentowa substancji.

−

Oprocentowanie oszcz

ę

dno

ś

ci i kredytów.

−

Podatki, podwy

ż

ki i obni

ż

ki.

−

Analiza diagramów i tabel.

−

Zadania ró

ż

ne.

Zadania praktyczne. Geometria.

−

Zamiana jednostek (równie

ż

u

ż

ywanych w innych dziedzinach ni

ż

geometria)

−

Czytanie mapy.

−

Planimetria zadania ró

ż

ne (tw Pitagorasa, trygonometria oraz inne)

−

Osie symetrii -

ś

rodki symetrii:

−

Stereometria

Zadania praktyczne.

Równania, nierówno

ś

ci, układy równa

ń

i inne…

−

Zadania zwykłe:

−

Zadania z wiekiem

−

Zadania geometryczne

−

Proporcjonalno

ść

−

Odszukiwanie liczb

−

Zadania ró

ż

ne

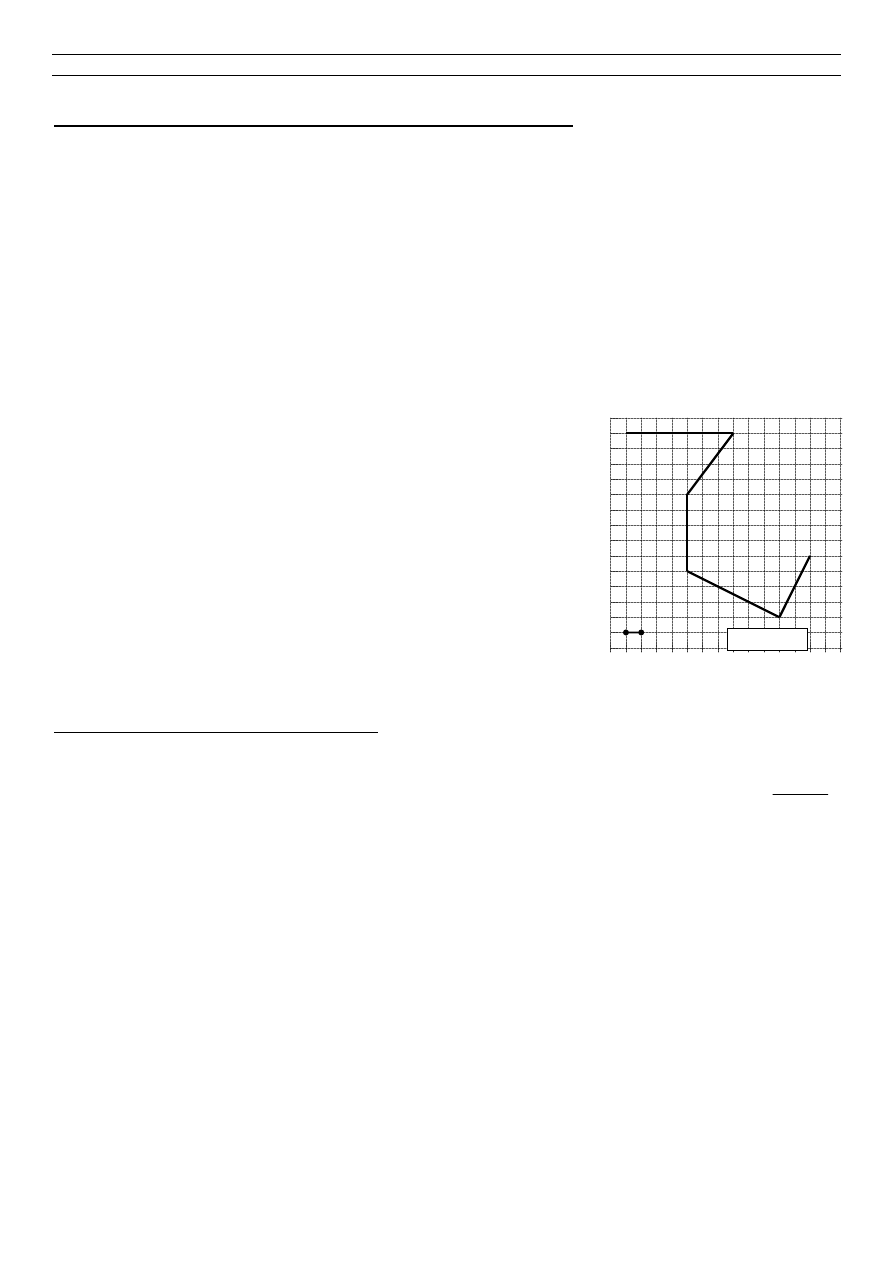
ZADANIA PRAKTYCZNE – FUNKCJE, WYRA

ś

ENIA, ANALIZA DANYCH

PREZENTACJA INFORMACJI ZA POMOC

Ą

WYRA

ś

E

Ń

ALGEBRAICZNYCH

1. Zapisz za pomoc

ą

wyra

ż

enia liczb

ę

o 5 wi

ę

ksz

ą

od połowy iloczynu liczb a i b.

2. Na parkingu stało x samochodów marki Fiat. Samochodów marki Trabant było o trzy wi

ę

cej ni

ż

Fiatów. Na tym

samym parkingu stały równie

ż

3 Fordy. Zapisz za pomoc

ą

wyra

ż

enia algebraicznego ilo

ść

samochodów na

parkingu.

3. W pewnej klasie uczy si

ę

x chłopców oraz y dziewcz

ą

t. Zapisz za pomoc

ą

wyra

ż

enia algebraicznego, które

przedstawiałoby ilo

ść

uczniów w klasie gdyby chłopców było o 4 mniej a dziewcz

ą

t byłoby dwa razy wi

ę

cej.

4. Gimnazjalny zespół muzyczny postanowił zorganizowa

ć

zabaw

ę

szkoln

ą

dla uczniów. Wynaj

ę

cie sali kosztuje 200

zł. Koszt wynaj

ę

cia zostanie podzielony równo mi

ę

dzy uczestników. Oprócz tej kwoty ka

ż

dy uczestnik wpłaci po 5

zł na soki, wod

ę

mineraln

ą

i krakersy. Oznacz przez n liczb

ę

uczestników i napisz wyra

ż

enie algebraiczne równe

kosztowi całej zabawy oraz wyra

ż

enie algebraiczne równe kosztowi uczestnictwa jednego ucznia (ile zapłaci

jeden ucze

ń

). Oblicz koszt uczestnictwa jednego ucznia w zabawie, je

ś

li we

ź

mie w niej udział 100 uczniów.

Oblicz, ilu uczniów wzi

ę

ło udział w zabawie, je

ś

li koszt uczestnictwa jednego ucznia był równy 9 zł?

5. Do Klubu Przyrodnika nale

ż

y a uczniów z klasy I. Uczniów z klasy II nale

ż

y

tyle samo co z klasy I, a z klasy III jest ich m razy wi

ę

cej ni

ż

z klasy I.

Przedstaw za pomoc

ą

wyra

ż

enia algebraicznego, ilu uczniów nale

ż

y do

klubu?

6. Na rysunku 1 zaznaczona jest trasa podró

ż

y. Zapisz jej długo

ść

za pomoc

ą

wyra

ż

enia algebraicznego przyjmuj

ą

c x jako jednostk

ę

.

7. W styczniu sprzeda

ż

samochodów w salonie motoryzacyjnym wyniosła x

złotych. W lutym sprzeda

ż

spadła o 25%, ale ju

ż

w marcu wzrosła dwukrotnie

w porównaniu z miesi

ą

cem wcze

ś

niejszym. Zapisz za pomoc

ą

wyra

ż

enia

sprzeda

ż

samochodów w pierwszym kwartale roku.

8. Wyprodukowan

ą

parti

ę

d

ż

emu pakowano do słoików o pojemno

ś

ciach 500

ml, 0,75 l i 1 l. Najmniejszych słoików było a, słoików

ś

rednich było o 50%

wi

ę

cej ni

ż

małych natomiast słoików du

ż

ych było 300. Zapisz wyra

ż

enie

algebraiczne prezentuj

ą

ce ilo

ść

wyprodukowanego d

ż

emu.

FUNKCJE I WARTO

Ś

CI LICZBOWE WYRA

ś

E

Ń

9. Narysuj wykres funkcji y = 2x – 3. Jakie jest miejsce zerowe tej funkcji?

10. Roczny koszt utrzymania rezerwatu w Białowieskim Parku Narodowym mo

ż

na wyliczy

ć

ze wzoru:

(gdzie k to roczny koszt, d - liczba drzew b

ę

d

ą

cych pomnikami przyrody). Oblicz roczny koszt utrzymania takiego

rezerwatu, je

ś

li w Białowieskim Parku Narodowym ro

ś

nie 1565 pomników przyrody.

11. Obwód prostok

ą

ta wynosi 20 cm. Zapisz za pomoc

ą

wzoru funkcji zale

ż

no

ść

mi

ę

dzy długo

ś

ci

ą

jednego boku,

a drugiego. Narysuj wykres tej funkcji (pami

ę

taj,

ż

e długo

ś

ci mog

ą

by

ć

tylko dodatnie).

12. Obserwuj

ą

c zu

ż

ycie benzyny w swoim samochodzie, pan Nowak stwierdził,

ż

e je

ś

li wystartuje z pełnym bakiem i

b

ę

dzie jechał po autostradzie ze stał

ą

pr

ę

dko

ś

ci

ą

, to zale

ż

no

ść

liczby litrów benzyny w baku (y) od liczby

przejechanych kilometrów (x) wyra

ż

a si

ę

wzorem: y = –0,05x + 45. Ile benzyny zostanie w baku po przejechaniu

200 km? Jak

ą

pojemno

ść

ma bak tego samochodu? Na przejechanie ilu kilometrów wystarczy pełny bak?

Przekształ

ć

tak wzór, aby przedstawiał zale

ż

no

ść

liczby przejechanych kilometrów od zu

ż

ytej benzyny.

13. Jeden m

3

wody kosztuje 2,70 zł. Zapisz wzór, który opisuje zale

ż

no

ść

wysoko

ś

ci opłaty od ilo

ś

ci zu

ż

ytej wody

(przy przyj

ę

tych oznaczeniach: x – ilo

ść

m

3

zu

ż

ytej wody, y – opłata za zu

ż

yt

ą

wod

ę

)? Narysuj wykres tej

zale

ż

no

ś

ci.

14. Wsiadaj

ą

c do taksówki licznik wskazuje osiem złotych (jako opłata za skorzystanie z taksówki), a potem za ka

ż

dy

przejechany kilometr płacimy 2 złote 50 groszy. Zaprezentuj t

ą

zale

ż

no

ść

za pomoc

ą

wzoru funkcji i narysuj jej

wykres. Ile pieni

ę

dzy zapłacimy za przejechanie 15 kilometrów? Jak daleko mo

ż

emy zajecha

ć

za 30 złotych

(około)?

Rysunek 1

x

2

55

32

−

=

d

k

-2

0

2

4

6

8

10

12

14

16

18

20

I

II

III

IV

V

VI

VII

VIII

IX

X

XI

XII

WYKRES TEMPERATURY ROCZNEJ

droga (km)

czas (min)

0

2

4

6

8

10

12

14

0

30

60

90

120

150

180

ODCZYTYWANIE INFORMACJI Z TABEL, WYKRESÓW I DIAGRAMÓW

15. Dwaj chłopcy wybrali si

ę

na wycieczk

ę

rowerow

ą

. Po powrocie do domu sporz

ą

dzili wykres przedstawiaj

ą

cy jej

przebieg. Przeanalizuj wykres i odpowiedz na pytania: Ile metrów przejechali chłopcy w ci

ą

gu pierwszych pół

godziny? Ile w sumie czasu po

ś

wi

ę

cili chłopcy na odpoczynek? Z jak

ą

pr

ę

dko

ś

ci

ą

jechali chłopcy podczas

drugiego odcinka podró

ż

y (po pierwszym odpoczynku)?

16. Przypatrz si

ę

na diagram prezentuj

ą

cy ceny biletów kolejowych na trasach o długo

ś

ciach wi

ę

kszych ni

ż

180 km.

Ile nale

ż

y zapłaci

ć

za trzy bilety do Warszawy (350 km)? Jak

ą

cen

ę

za bilet do Wrocławia (190 km) zapłaci

student korzystaj

ą

cy ze zni

ż

ki 30%?

17. Na wykresie przedstawiono roczny przebieg

temperatury powietrza oraz

ś

rednie temperatury

miesi

ę

czne

(w

stopniach

Celsjusza)

zanotowane

w

jednej

ze

stacji

meteorologicznych

pobrze

ż

a

Bałtyku.

Odpowiedz na pytania: Ile wynosi

ś

rednia

temperatura

w

miesi

ą

cach

wakacyjnych

(czerwiec, lipiec, sierpie

ń

)? Ile wynosi roczna

amplituda

(ró

ż

nica)

temperatury

powietrza

zanotowana przez t

ę

stacj

ę

meteorologiczn

ą

?

C

e

n

a

(

P

L

N

)

27

28

29

30

31

32

33

34

35

36

37

181 - 200

201 - 220

221 - 240

241 - 260

261 - 290

291 - 320

321 - 360

Odległo

ść

(km)

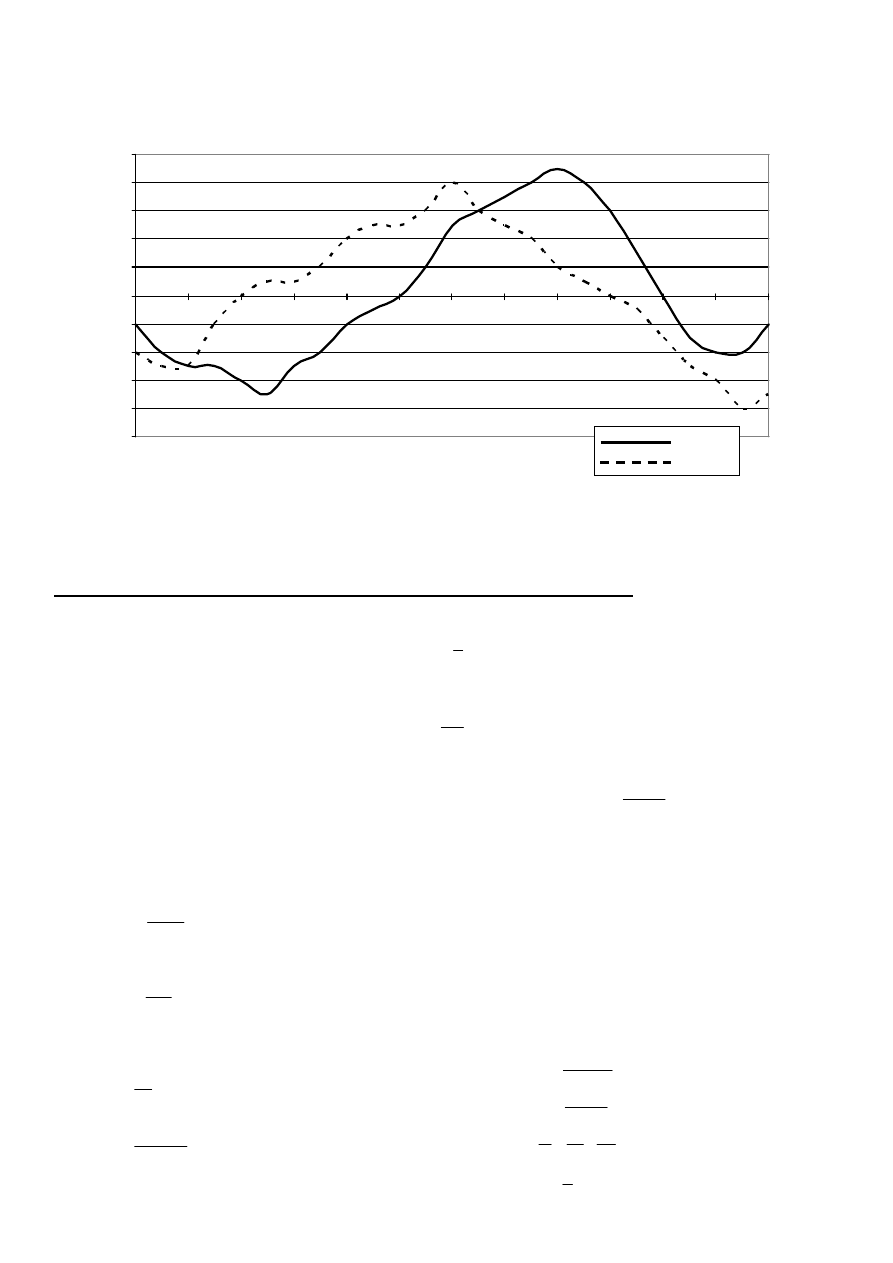
18. Przypatrz si

ę

na wykres przedstawiaj

ą

cy dzienne zmiany temperatury dwóch miastach Polski. Odpowiedz na

pytania: Jak

ą

temperatur

ę

zanotowano 0 8.00 w Krakowie, a jak

ą

w Łodzi? Przez ile godzin notowano wy

ż

sz

ą

temperatur

ę

w Łodzi ni

ż

w Krakowie? Ile wynosiła najwy

ż

sza temperatura dnia w Krakowie, i o której godzinie j

ą

zanotowano? Podaj godzin

ę

, o której zmierzono temperatur

ę

0° w Łodzi.

19. Oblicz

ś

redni

ą

arytmetyczn

ą

liczb: -3, 16, 2, 2, -11.

20. Wska

ż

median

ę

zbioru liczb: {0, 4, 4, 6, -3, -2, 1, 2, 1, 5, -10}.

21. Zapisz za pomoc

ą

wyra

ż

enia algebraicznego

ś

redni

ą

arytmetyczn

ą

liczb: x, 2x i x

2

.

PRZEKSZTAŁCANIE WZORÓW I MATEMATYKA W ZAGADNIENIACH FIZYCZNYCH

22. Pr

ę

dko

ść

w ruchu jednostajnym wyra

ż

a si

ę

wzorem

t

s

v

=

(v – pr

ę

dko

ść

, s – droga, t - czas). Przekształ

ć

wzór do

postaci wzoru przedstawiaj

ą

cego drog

ę

w zale

ż

no

ś

ci od czasu i pr

ę

dko

ś

ci.

23. Spadek swobodny ciała mo

ż

na opisa

ć

wzorem:

2

2

gt

h

=

, gdzie h oznacza wysoko

ść

, z której ciało spada, g -

przyspieszenie ziemskie, a t - czas spadania. Przekształ

ć

wzór tak, aby przedstawiał on czas spadania (t).

24. Wzór na przyspieszenie w ruchu jednostajnie przyspieszonym opisuje wzór

t

v

v

a

1

2

−

=

, gdzie v

1

i v

2

oznaczaj

ą

odpowiednio pr

ę

dko

ś

ci pocz

ą

tkow

ą

i ko

ń

cow

ą

, t oznacza czas natomiast a to przyspieszenie. Przekształ

ć

wzór

tak, aby przedstawiał pr

ę

dko

ść

pocz

ą

tkow

ą

.

25. Przekształ

ć

wzór tak aby otrzyma

ć

wzór na wielko

ść

zapisan

ą

w nawiasie:

)

(

2

k

t

k

r

H

−

=

26. Przekształ

ć

wzór tak aby otrzyma

ć

wzór na wielko

ść

zapisan

ą

w nawiasie:

)

t

(

at

S

2

2

=

27. Przekształ

ć

wzory tak by obliczy

ć

wielko

ść

podan

ą

w nawiasie:

(

)

)

(

)

(

2

)

(

2

2

)

(

2

h

mgh

E

a

h

b

a

P

a

b

a

O

h

ah

P

=

⋅

+

=

+

=

=

)

(

)

(

1

1

1

)

(

2

)

(

3

2

2

2

1

1

1

2

t

m

t

a

S

R

R

R

R

g

s

gt

c

m

x

r

x

x

A

+

=

+

=

−

=

−

=

-10

-8

-6

-4

-2

0

2

4

6

8

10

0:00

2:00

4:00

6:00

8:00

10:00

12:00

14:00

16:00

18:00

20:00

22:00

0:00

KRAKÓW

ŁÓD

Ź

ZADANIA PRAKTYCZNE – PROCENTY

ST

Ęś

ENIA PROCENTOWE ROZTWORÓW, ZAWARTO

ŚĆ

PROCENTOWA SUBSTANCJI

1. Ile soli nale

ż

y rozpu

ś

ci

ć

w wodzie, aby otrzyma

ć

400 gramów roztworu o st

ęż

eniu 10%?

2. Zmieszano ze sob

ą

60 gramów cukru i 240 gramów wody. Jakie jest st

ęż

enie procentowe otrzymanego roztworu?

3. Ile nale

ż

y dosypa

ć

soli do 400 gramów wody, aby otrzyma

ć

roztwór o st

ęż

eniu 20%?

4. 15% wagi buraków stanowi cukier. Ile cukru mo

ż

na uzyska

ć

z 800 kg buraków?

5. St

ęż

enie roztworu kwasu wynosi 5%. Ile czystego kwasu, a ile wody nale

ż

ałoby zmiesza

ć

, aby otrzyma

ć

0,2 litra

roztworu?

6. Do 200 gramów roztworu soli o st

ęż

eniu 5% dosypano jeszcze 50 gramów soli. Jakie st

ęż

enie ma otrzymany

roztwór?

7. W szklance znajduje si

ę

250 g dziesi

ę

cioprocentowego roztworu octu. Marynuj

ą

c grzyby powinni

ś

my u

ż

y

ć

octu o

st

ęż

eniu 5%. Ile nale

ż

y dola

ć

wody do szklanki, aby otrzyma

ć

takie st

ęż

enie?

8. Mleko zawiera 1,5% tłuszczu. Ile gramów tłuszczu znajduje si

ę

w kartonie zawieraj

ą

cym 2 kg mleka?

9. Ile wody nale

ż

ałoby doda

ć

do 1 kg pi

ę

tnastoprocentowego roztworu cukru, aby otrzyma

ć

roztwór o st

ęż

eniu 10%?

10. Zmieszano ze sob

ą

dwa roztwory kwasów o st

ęż

eniach 10% i 20% i w wyniku zmieszania otrzymano 500g

roztworu o st

ęż

eniu 14%. Ile wa

ż

ył ka

ż

dy ze zmieszanych kwasów?

OPROCENTOWANIE OSZCZ

Ę

DNO

Ś

CI I KREDYTÓW

11. Ile wynios

ą

roczne odsetki od kwoty 2000 złotych, zło

ż

onej na koncie w banku, w którym oprocentowanie lokat

wynosi 4,5% w skali roku?

12. Ile pieni

ę

dzy na koncie b

ę

dzie mie

ć

klient, który wpłaci na rok kapitał wynosz

ą

cy 10000 złotych. Bank oferuje

oprocentowanie lokat w wysoko

ś

ci 6% w skali roku.

13. Wpłacaj

ą

c do banku kwot

ę

4000 złotych po roku czasu b

ę

dziemy mie

ć

na koncie 4280 złotych. Oblicz, jakie jest

oprocentowanie lokat w tym banku?

14. Stopa procentowa lokat w banku X wynosi 20%. Oblicz, ile pieni

ę

dzy b

ę

dziesz mie

ć

na koncie po dwóch latach

oszcz

ę

dzania wpłacaj

ą

c 5000 złotych?

15. W pewnym banku roczne odsetki od kapitału 800 złotych wynosz

ą

60 złotych. Oblicz, jakie oprocentowanie lokat

proponuje ten bank?

16. Kupuj

ą

c aparat cyfrowy na raty, klient zdecydował si

ę

na 12 miesi

ę

cznych rat. Wiadomo,

ż

e aparat kosztuje 1200

złotych, lecz do ka

ż

dej raty nale

ż

y jeszcze doliczy

ć

10% odsetek. Oblicz, ile klient b

ę

dzie musiał jeszcze spłaci

ć

pieni

ę

dzy, je

ś

li do tej pory udało mu si

ę

spłaci

ć

pi

ęć

rat.

17. Ile na koncie ma obecnie pan Kowalski, je

ś

li trzy lata temu wpłacił 500 złotych, a oprocentowanie lokat wynosiło

6% w skali roku (wynik zaokr

ą

glij)? O ile procent wi

ę

cej pieni

ę

dzy ma na koncie Kowalski w porównaniem z

kwot

ą

, któr

ą

wpłacał trzy lata temu?

18. Firma BENATA po

ż

yczyła w Banku Kredytowym 20000 złotych na remont i modernizacj

ę

zakładu na okres dwóch

lat. Odsetki w stosunku rocznym wynosz

ą

30%. Jak

ą

kwot

ę

b

ę

dzie musiała wpłaci

ć

ta firma do banku?

PODATKI, PODWY

ś

KI I OBNI

ś

KI

19. Ka

ż

dy pracownik musi zapłaci

ć

podatek od wynagrodzenia w wysoko

ś

ci 30%. Ile musi zapłaci

ć

podatku

pracownik, którego pensja (brutto) wynosi 2000 złotych? Jaka wypłat

ę

(netto) otrzyma ten pracownik?

20. Po sezonie ceny w sklepie obni

ż

ono o 20%. Ile nale

ż

y zapłaci

ć

za spodnie, które przed obni

ż

k

ą

kosztowały 120

złotych?

21. Ceny akcji firmy X wzrosły w ci

ą

gu dnia o 2%. Ile kosztuje teraz akcja firmy, je

ś

li wczoraj płacono za jedn

ą

2,5 zł?

22. Cena nart w sklepie MAX SPORT wzrosła z 800 złotych do 920. O ile procent nast

ą

piła podwy

ż

ka?

23. Cen

ę

kurtek podwy

ż

szono przed sezonem o 10%, a po sezonie obni

ż

ono o 10%. Ile kosztuje po sezonie kurtka,

która przed sezonem kosztowała 400 złotych?

24. Podatek VAT wynosi 23% ceny netto wi

ę

kszo

ś

ci produktów i usług. Ile podatku (około) nale

ż

y zapłaci

ć

od ceny

telewizora sprzedanego za 1800 złotych. Uwaga! Cena sprzeda

ż

y, to cena brutto, czyli cena powstała przez

dodanie do ceny netto podatku VAT?

25. Ceny w sklepie obni

ż

ono o 5%. Ile kosztował dawniej odtwarzacz DVD, który obecnie kosztuje 570 złotych?

26. Akcje firmy BUZER zanotowały spadek o 5% a nast

ę

pnie wzrosły o 4%. Ile kosztuj

ą

obecnie akcje tej firmy, je

ś

li

wcze

ś

niej trzeba było za nie zapłaci

ć

12 złotych (wynik podaj z dokładno

ś

ci

ą

do jednego grosza).

27. Legitymacja studencka uprawnia do przejazdów kolej

ą

korzystaj

ą

c ze zni

ż

ki 40% od ceny biletu. Przeanalizuj

cennik i odpowiedz na poni

ż

sze pytania (cennik i zasady nie pokrywaj

ą

si

ę

z PKP):

Długo

ść

trasy

Ceny biletów poci

ą

g zwykły

Ceny biletów poci

ą

g po

ś

pieszny

Klasa 1

Klasa 2

Klasa 1

Klasa 2

0 – 50 km

10 zł

8 zł

15 zł

10 zł

51 – 100 km

15 zł

12 zł

20 zł

15 zł

101 – 150 km

20 zł

16 zł

25 zł

18 zł

151 – 200 km

25 zł

20 zł

30 zł

22 zł

201 – 250 km

32 zł

25 zł

35 zł

27 zł

UWAGA: Ceny biletów poci

ą

gów ekspresowych równaj

ą

si

ę

cenom

obowi

ą

zuj

ą

cym dla poci

ą

gów po

ś

piesznych z t

ą

ró

ż

nic

ą

,

ż

e do ka

ż

dego biletu

nale

ż

y wykupi

ć

miejscówk

ę

w cenie 10 złotych (miejscówki nie s

ą

obj

ę

te zni

ż

k

ą

)

Pytanie 1: Ile pieni

ę

dzy zapłaci student na trasie Katowice – Kraków (78 km) poci

ą

giem zwykłym w wagonie

klasy drugiej?
Pytanie 2: Ile kosztuje bilet na trasie Kraków Zakopane (135 km) dla studenta, który zdecyduje si

ę

wykupi

ć

bilet na poci

ą

g ekspresowy w wagonie klasy pierwszej.

28. Przeczytaj cennik biletów do kina i odpowiedz na pytanie:

Która grupa zapłaci wi

ę

cej za bilety do kina: Pierwsza, w której jest dwóch dorosłych i pi

ę

cioro dzieci, czy

druga, w której jest jeden dorosły i dziesi

ę

cioro dzieci?

ANALIZA DIAGRAMÓW I TABEL


29. Diagram przedstawia skład szynki. Odpowiedz na pytania:

25%

35%

30%

10%

Białko

Tłuszcze

Woda

Sole mineralne

Pytanie 1: Ile białek znajduje si

ę

w 2,5 kg szynki?

Pytanie 2: Ile soli mineralnych zawiera 20 dag szynki?
Pytanie 3: Ile mo

ż

na zje

ść

szynki, aby nie dostarczy

ć

do organizmu wi

ę

cej ni

ż

0,7 dag tłuszczu?

30. Tabela przedstawia zmiany ilo

ś

ci mieszka

ń

ców dwóch miast w poszczególnych latach:

Rok

Nowy Bór

Stary Bór

1980

125 tys.

112 tys.

1990

143 tys.

142 tys.

2000

165 tys.

177 tys.

Odpowiedz na pytania (wyniki zaokr

ą

glij z dokładno

ś

ci

ą

do jednego procentu):

Pytanie 1: O ile procent wzrosła ilo

ść

mieszka

ń

ców Nowego Boru w latach 1980 – 1990?

Pytanie 2: O ile procent mniej mieszka

ń

ców liczył w 2000 roku Nowy Bór w porównaniu ze Starym Borem?

KINO APOLLO – CENY BILETÓW:

BILET NORMALNY – 10 złotych
BILET ULGOWY (dzieci do lat 15) – 8 złotych

Grupy powy

ż

ej 10 osób – zni

ż

ka 40%

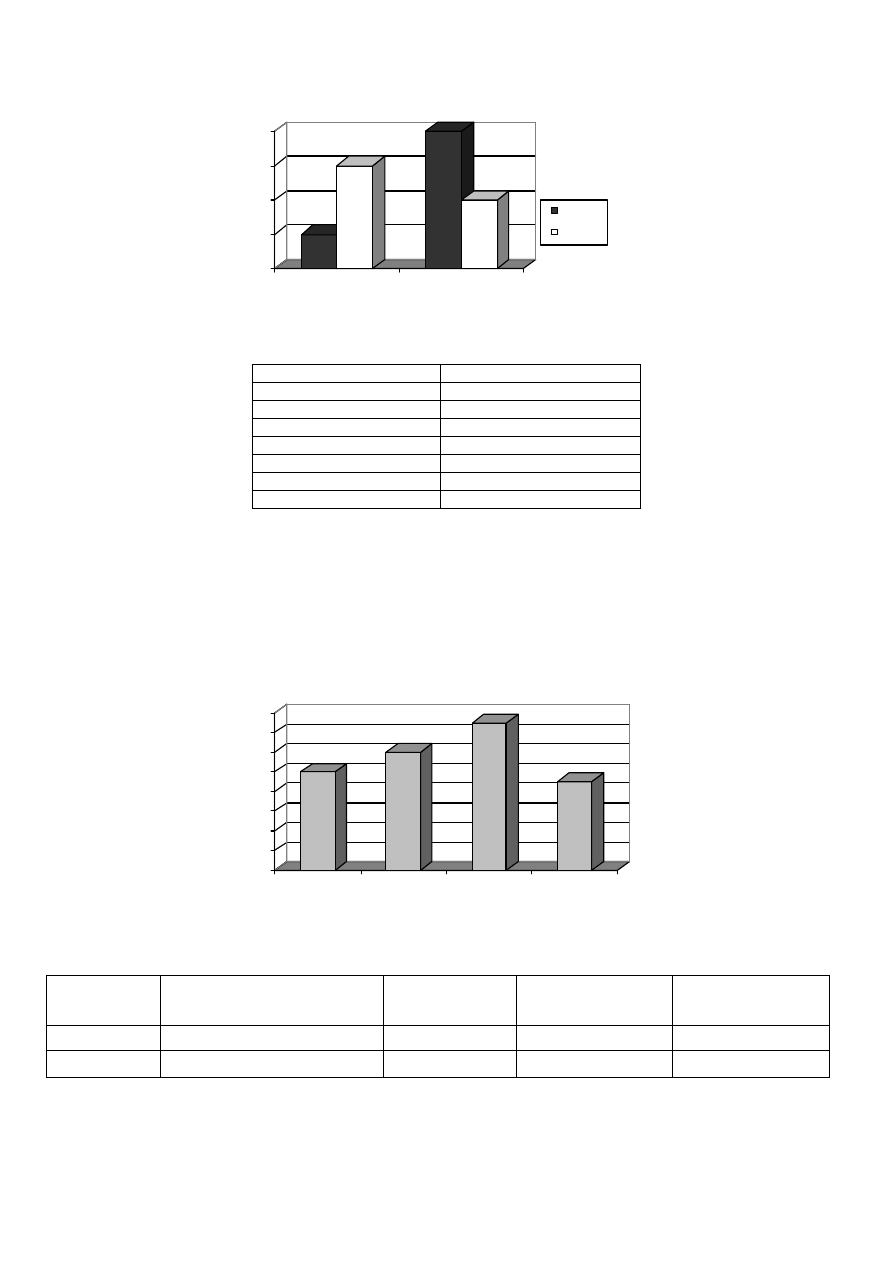
31. Diagram przedstawia wyniki głosowania na dwóch kandydatów w wyborach na burmistrza: Wiedz

ą

c,

ż

e Miasto 1

ma 100 tys. mieszka

ń

ców, a Miasto 2 ma 200 tys. mieszka

ń

ców oblicz, kto wygrał wybory?

32. Tabela przedstawia powierzchnie poszczególnych kontynentów:

Kontynent

Powierzchnia

Europa

9 763 000 km

2

Afryka

29 853 000 km

2

Azja

44 406 000 km

2

Ameryka Północna

24 298 000 km

2

Ameryka Południowa

17 684 000 km

2

Australia I Oceania

8 936 000 km

2

Antarktyda

13 176 000 km

2

Polecenie 1: Zaokr

ą

glij powierzchnie kontynentów z dokładno

ś

ci

ą

do jednej dziesi

ą

tej miliona.

Polecenie 2: Ile razy (w przybli

ż

eniu) powierzchnia Azji jest wi

ę

ksza od Europy?

Polecenie 3: Ile procent powierzchni wszystkich l

ą

dów zajmuje kontynent Afryka

ń

ski?

Polecenie 4:O ile procent wi

ę

ksza jest powierzchnia Azji ni

ż

Ameryki Południowej?

33. Diagram przedstawia ilo

ść

uczniów klas pierwszych pewnej szkoły w poszczególnych latach. Przeanalizuj

diagram i odpowiedz na pytania:

Pytanie 1: O ile procent wi

ę

cej pierwszoklasistów uczyło si

ę

w tej szkole w 2002 roku ni

ż

w 2001?

Pytanie 2: O ile procent zmalała liczba pierwszoklasistów w latach 2003 – 2004?

34. Tabela przedstawia rozkład zagospodarowania terenów dwóch wsi na polskim Podhalu. Przypatrz si

ę

danym i

odpowiedz na pytania:

Wie

ś

Powierzchnia całkowita w km

2

Lasy

Pola uprawne

Ł

ą

ki

D

ę

bno

12

25%

40%

20%

Grywałd

8

30%

25%

25%

Pytanie 1: Jak

ą

powierzchni

ę

w hektarach maj

ą

lasy D

ę

bna, a jak

ą

Grywałdu?

Pytanie 2: O ile punktów procentowych wi

ę

cej pól uprawnych jest na terenie D

ę

bna ni

ż

Grywałdu?

Pytanie 3: W której wsi wi

ę

ksz

ą

powierzchni

ę

zajmuj

ą

ł

ą

ki?

0%

20%

40%

60%

80%

Kowalski

Nowak

Miasto 1

Miasto 2

0

10

20

30

40

50

60

70

80

2001

2002

2003

2004

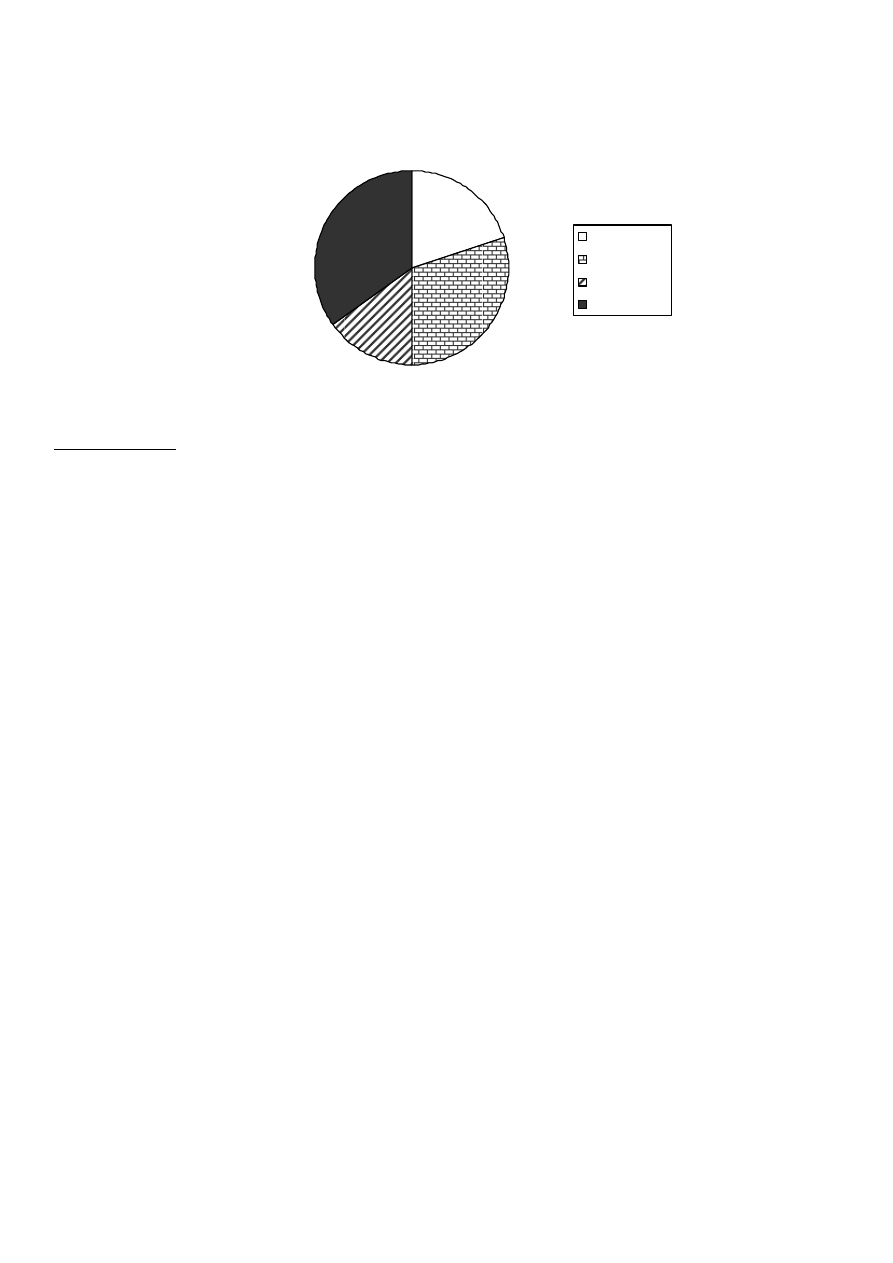
35. Diagram kołowy prezentuje procentowy rozkład tematyki ksi

ąż

ek w ksi

ę

garni. Przeanalizuj diagram i odpowiedz

na pytania:

Pytanie 1: Ile procent zbiorów zajmuj

ą

ksi

ąż

ki przyrodnicze?

Pytanie 2: O ile punktów procentowych wi

ę

cej jest ksi

ąż

ek przyrodniczych ni

ż

kryminałów?

Pytanie 3: Ile ksi

ąż

ek jest w ksi

ę

garni, je

ś

li znajduje si

ę

tam 450 kryminałów?

ZADANIA RÓ

ś

NE

36. Na kolonii letniej podczas dnia sportu 30% dzieci wzi

ę

ło udział w zawodach pływackich, a o czterech uczniów

mniej uczestniczyło w zawodach lekkoatletycznych. Pozostałych dwudziestu czterech uczniów grało w piłk

ę

no

ż

n

ą

. Ile dzieci uczestniczyło w tych zaj

ę

ciach sportowych?

37. Prostok

ą

t ma wymiary 4 cm i 12 cm. O ile procent zwi

ę

kszy si

ę

pole prostok

ą

ta, je

ś

li ka

ż

dy z jego boków

zwi

ę

kszymy o 25%?

38. W równoległoboku miara k

ą

ta ostrego stanowi 20% miary k

ą

ta rozwartego. Znajd

ź

miary tych k

ą

tów.

39. W szkole uczy si

ę

780 uczniów. Dziewcz

ą

t jest o 60% wi

ę

cej ni

ż

chłopców. Ile dziewcz

ą

t a ile chłopców uczy si

ę

w tej szkole?

40. Pieni

ą

dze z wypłaty pan Nowak przeznaczył na ró

ż

ne potrzebne wydatki. 40% pensji pochłon

ę

ły opłaty za

mieszkanie. Dwa razy mniejsz

ą

sum

ę

przeznaczył na zakup nowego magnetofonu, a 40 złotych stanowiła rata

spłacana za kupiony w zeszłym roku telewizor. W chwili obecnej pozostało panu Nowakowi 600 złotych. Ile
wynosiła pensja pana Nowaka?

41. Inflacja w Polsce w roku 2000 wynosiła 6,4%, a w roku 2001 5,6%. O ile punktów procentowych zmniejszyła si

ę

inflacja w tych latach?

42. Ostrosłup i graniastosłup maj

ą

identyczne podstawy w kształcie kwadratu o boku 10 cm i takie same wysoko

ś

ci

równe 12 cm. O ile procent obj

ę

to

ść

ostrosłupa jest mniejsza od obj

ę

to

ś

ci graniastosłupa?

43. Wła

ś

ciciel sklepu ze sprz

ę

tem sportowym zakupił w hurtowni 10 rowerów, ka

ż

dy w cenie 500 złotych. Ustalaj

ą

c

cen

ę

detaliczn

ą

rowerów wła

ś

ciciel doda do ceny hurtowej 30% mar

ż

y. Ile zarobi na sprzeda

ż

y wszystkich

rowerów, je

ś

li podatek od ka

ż

dego sprzedanego towaru wynosi 20% (licz

ą

c z ceny sprzeda

ż

y)?

44. Jacek i Staszek zbieraj

ą

widokówki. Jeszcze wczoraj Staszek miał dwa razy mniej pocztówek ni

ż

Jacek, ale dzi

ś

maj

ą

tyle samo, gdy

ż

Jacek sprzedał na giełdzie 15 sztuk, a Staszek powi

ę

kszył swoj

ą

kolekcj

ę

a

ż

o 70%. Ile

widokówek miał wczoraj ka

ż

dy z chłopców?

45. 20% całej ksi

ąż

ki stanowi rozdział pierwszy, a rozdział drugi ma o 8 stron wi

ę

cej, rozdział trzeci to 30% całej

ksi

ąż

ki, natomiast ostatni rozdział ma tyle samo co drugi. Ile stron ma ksi

ąż

ka?

46. 20% uczniów klasy było na wakacjach nad morzem. 15% pozostałych uczniów sp

ę

dziło wakacje w górach. W

ś

ród

pozostałych uczniów siedmiu wybrało si

ę

nad jeziora, a dziesi

ę

ciu pozostało w domach. Ilu uczniów liczyła ta

klasa?

47. Trzem laureatom ( I, II, III miejsce) Konkursu Wiedzy o Unii Europejskiej ufundowano nagrody pieni

ęż

ne. Nagroda

II była o 20% mniejsza od I, a III stanowi 60% warto

ś

ci I. Na nagrody przeznaczono ł

ą

cznie 120 euro. Oblicz, ile

euro dostał ka

ż

dy laureat tego konkursu. Zapisz obliczenia.

48. Turysta miał do przebycia długa tras

ę

. Pierwszego dnia pokonał całej trasy. Drugiego dnia udało mu si

ę

pokona

ć

60% pozostałej cz

ęś

ci trasy. Na trzeci dzie

ń

zostało mu jeszcze do przej

ś

cia 32 km. Jakiej długo

ś

ci była trasa?

20%

30%

15%

Przygodowe

Kryminały

Lektury

Przyrodnicze

ZADANIA PRAKTYCZNE – GEOMETRIA

ZAMIANA JEDNOSTEK (równie

ż

u

ż

ywanych w innych dziedzinach ni

ż

geometria)

1. Zamie

ń

jednostki długo

ś

ci:

3 m = …………………..…… cm
4,6 dm = ………………..….. cm
0,4 km = ……………………….m
5 cm = ………………………..dm
67,5 mm = …………………...cm
8000000 cm = ……………… km
4600 m = ……………………..km

2. Zamie

ń

jednostki pola:

30 cm

2

= …………………….. dm

2

680 m

2

= …………………………a

9 ha = …………………….………a
4000 cm

2

= …………………...dm

2

5,7 dm

2

= ……………….…… cm

2

89,5 cm

2

=………………..…….m

2

0,006 km

2

= …………….……...ha

3. Zamie

ń

jednostki obj

ę

to

ś

ci:

20 l =…………………………. dm

3

1500m

3

= ……………………. dm

3

36700 ml =……………..…………l
0,07 cm

3

=…………………….mm

3

30000 l = ………………………..m

3

0,00056 m

3

= …………….….. cm

3

600 l = ……………………………hl

4. Zamie

ń

jednostki czasu:

3,5 godziny ile to minut?
40 minut, jaka to cz

ęść

godziny?

1380 sekund, ile to minut?
Dwie doby i 7 godzin, ile to godzin?
0,25 minuty, ile to sekund?
5,2 godziny ile to minut?
0,04 godziny ile to sekund?

5. Zamie

ń

jednostki masy:

67 dag = ………………………….g
0,3 kg = ………………..………dag
12 t = ………………..…………..kg
0,09 g = ……………………….dag
8,65 dag = …………..…………..g
6500000 kg = ………..…………..t
5 g = ……………….……………kg

6. Zamie

ń

jednostki monetarne:

4,60 zł = ……………….………..gr
7 gr = …………………..………..zł
450 gr = …………………………zł
9,6 zł = …………..……………..gr

CZYTANIE MAPY


7. Najdłu

ż

sza rzeka w Polsce, Wisła ma 1047 km długo

ś

ci. Jaka jest jej długo

ść

na mapie w skali 1:3000000? Wynik

podaj w przybli

ż

eniu z dokładno

ś

ci

ą

do jednego milimetra.

8. Ile razy powierzchnia Parku Kampinoskiego na mapie w skali 1 : 500000 jest mniejsza od rzeczywistej

powierzchni tego parku? Wynik przedstaw za pomoc

ą

notacji wykładniczej.

9. Odległo

ść

mi

ę

dzy miejscowo

ś

ciami Babimost i Kargowa wynosi 12 km. Na mapie ta odległo

ść

to 3 cm. O ile

kilometrów s

ą

oddalone od siebie dwie inne miejscowo

ś

ci, je

ż

eli na tej samej mapie odległo

ść

mi

ę

dzy nimi wynosi

4 cm?

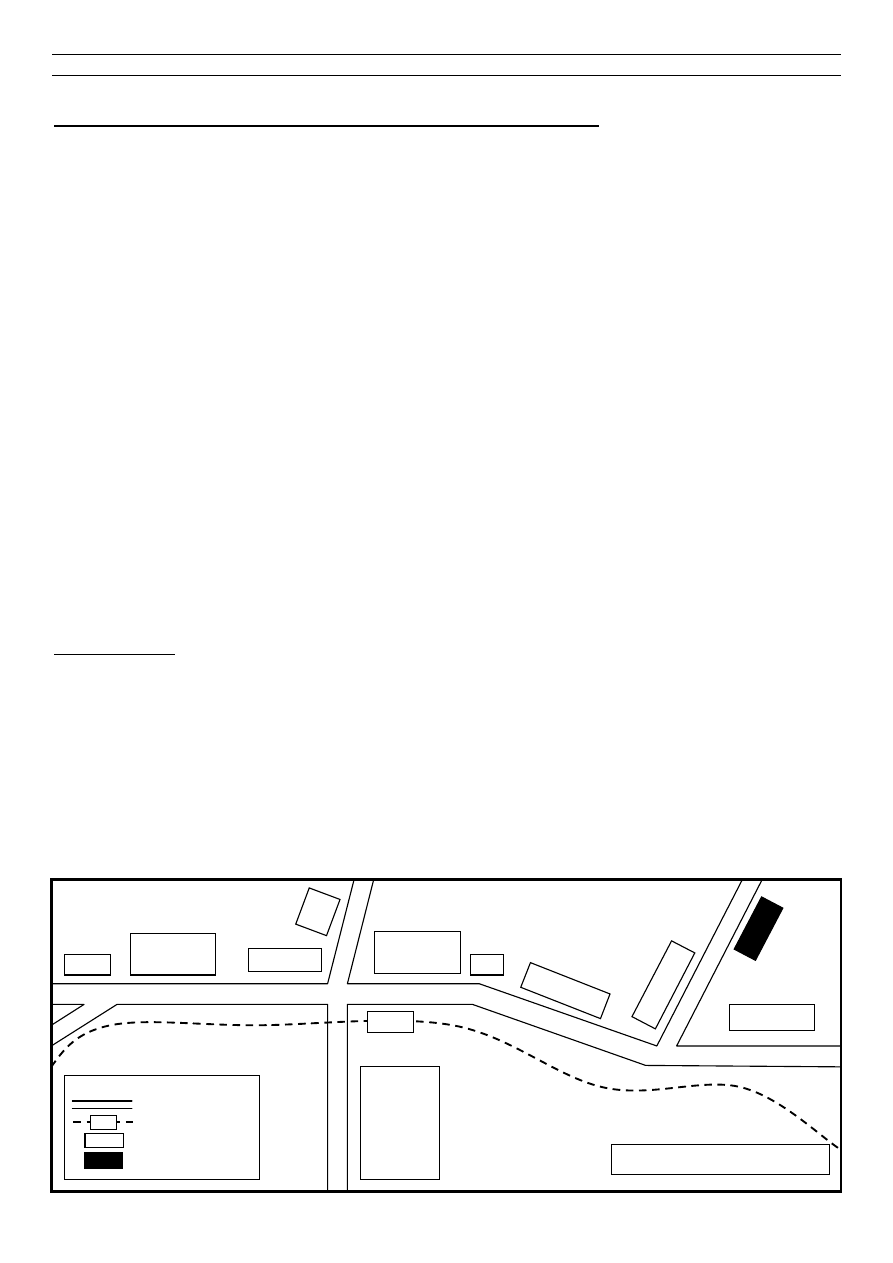
10. Tury

ś

ci po wyj

ś

ciu z dworca zatrzymali si

ę

na skrzy

ż

owaniu. Chc

ą

doj

ść

do schroniska. Jak

ą

odległo

ść

musz

ą

pokona

ć

? Wykonaj pomiar za pomoc

ą

linijki. Wynik mo

ż

na zaokr

ą

gli

ć

.

Legenda:
ulice
poci

ą

g, stacje

budynki
schroniska

Skala mapy 1 : 10000

PLANIMETRIA ZADANIA RÓ

ś

NE (TW PITAGORASA, TRYGONOMETRIA ORAZ INNE)

11. Trawnik, który ma kształt prostok

ą

ta o wymiarach 45 m i 20 m, postanowiono przedzieli

ć

kwiatow

ą

grz

ą

dk

ą

.

Rozwa

ż

ano dwa projekty (rysunek 2).

Granice mi

ę

dzy trawnikami i grz

ą

dk

ą

biegn

ą

wzdłu

ż

linii prostych i maj

ą

by

ć

umocnione kraw

ęż

nikami. Przed

posadzeniem kwiatów trzeba wysypa

ć

na grz

ą

dk

ę

warstw

ę

ziemi próchniczej grubo

ś

ci 20 cm. Przyj

ę

to projekt I.

Oblicz ł

ą

czn

ą

długo

ść

kraw

ęż

ników potrzebnych do oddzielenia grz

ą

dki od trawnika. Ile metrów sze

ś

ciennych

próchniczej ziemi trzeba wysypa

ć

na grz

ą

dk

ę

? Jakie byłyby, w porównaniu z projektem I, koszty zakupu ziemi

próchniczej a jakie kraw

ęż

ników, gdyby wybrano projekt II (mniejsze, wi

ę

ksze, czy takie same)?

12. Z portu wypłyn

ę

ły jednocze

ś

nie dwa statki badawcze: jeden na północ z pr

ę

dko

ś

ci

ą

24 w

ę

złów, drugi na wschód z

pr

ę

dko

ś

ci

ą

18 w

ę

złów (jeden w

ę

zeł jest to jedna mila morska (na godzin

ę

). Jaka b

ę

dzie odległo

ść

mi

ę

dzy

statkami po 1 godzinie

ż

eglugi?

13. Obwód pnia jednego z d

ę

bów na pewnej wysoko

ś

ci nad ziemi

ą

wynosi 7,85 m. Oblicz promie

ń

przekroju pnia na

tej wysoko

ś

ci.

14. Uczestnicy w

ę

drówki maj

ą

i

ść

w kierunku południowo-wschodnim. Igła busoli wskazuje kierunek północny. Ile

stopni ma k

ą

t rozwarty, którego ramionami s

ą

igła busoli i kierunek w

ę

drówki?

15. W rozpadlinie skalnej powstało jeziorko, którego powierzchnia ma kształt koła o

ś

rednicy 20 m. Oblicz pole powierzchni tego koła. Podaj wynik przybli

ż

ony.

16. Koło rowerowe o obwodzie 2 metrów wykonuje na pewnym odcinku drogi 550

obrotów. Ile pełnych obrotów wykona na tej samej drodze koło o obwodzie 1,5
metra?

17. Z trapezu równoramiennego wyci

ę

to koło o

ś

rednicy przystaj

ą

cej do wysoko

ś

ci

(rysunek 3). Rami

ę

trapezu ma długo

ść

równ

ą

krótszej podstawie. Przyjmuj

ą

c,

ż

e a = 5 cm, h = a – 1, b = 2a, oblicz pole zamalowanej figury. Wynik przedstaw

z dokładno

ś

ci

ą

do jedno

ś

ci.

18. Na jakiej wysoko

ś

ci siedzi ptak na rysunku 4?

19. Oblicz, na jakiej wysoko

ś

ci znajduje si

ę

dach domu o który oparta jest drabina długo

ś

ci 12 m (patrz rysunek 5)

Z – ziemia próchnicza
K – kwiaty

Rysunek 1

Z K Z

Z K Z

PROJEKT 1

PROJEKT 2

5 m 15 m

5 m 30 m

5 m 20 m

5 m 20 m

Rysunek 2

Rysunek 3

b

h

a

Rysunek 4

30°

12 m

9 m

1 m

Rysunek 5

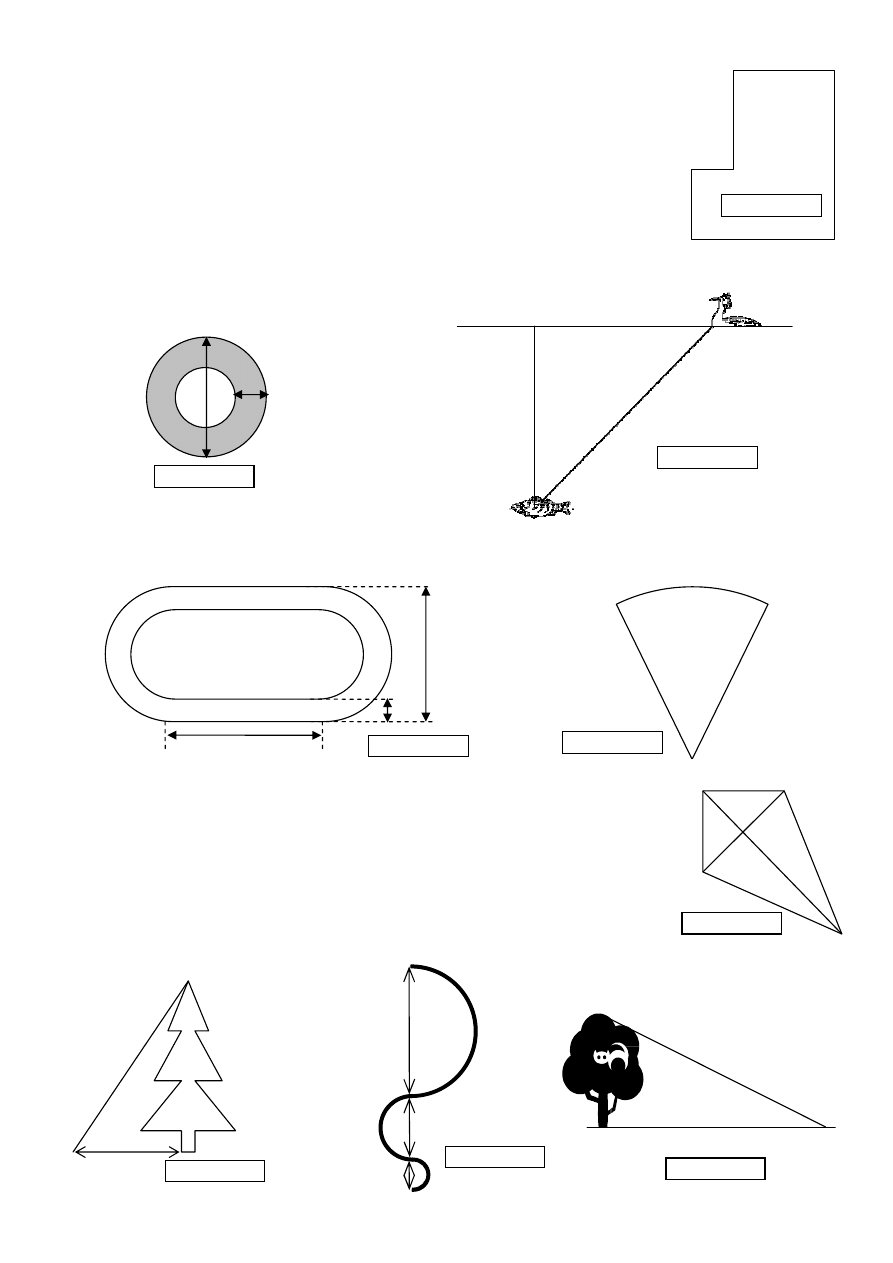
Rysunek 11

S

B

C

A

D

20. Rysunek 6 przedstawia plan podłogi jadalni w hotelu. Oblicz koszt wymiany podłogi,

je

ż

eli firma budowlana otrzymała 85 zł za wykonanie remontu 1 m

2

powierzchni.

21. Prostok

ą

tny trawnik o wymiarach 4 m na 5 m otoczono alejk

ą

, której szeroko

ść

wynosiła jeden metr. Oblicz powierzchni

ę

tej alejki. Ile asfaltu nale

ż

y poło

ż

y

ć

na tej

alejce, je

ś

li na jeden metr kwadratowy powierzchni potrzebne jest 35 litrów asfaltu?

22. Na miejscu dawnego skrzy

ż

owania postanowiono wybudowa

ć

rondo, którego

wymiary (w metrach) podane s

ą

na rysunku. Oblicz, na jakiej powierzchni trzeba

wyla

ć

asfalt (obszar zacieniowany na rysunku 7). W swoich obliczeniach za

π

podstaw 3)

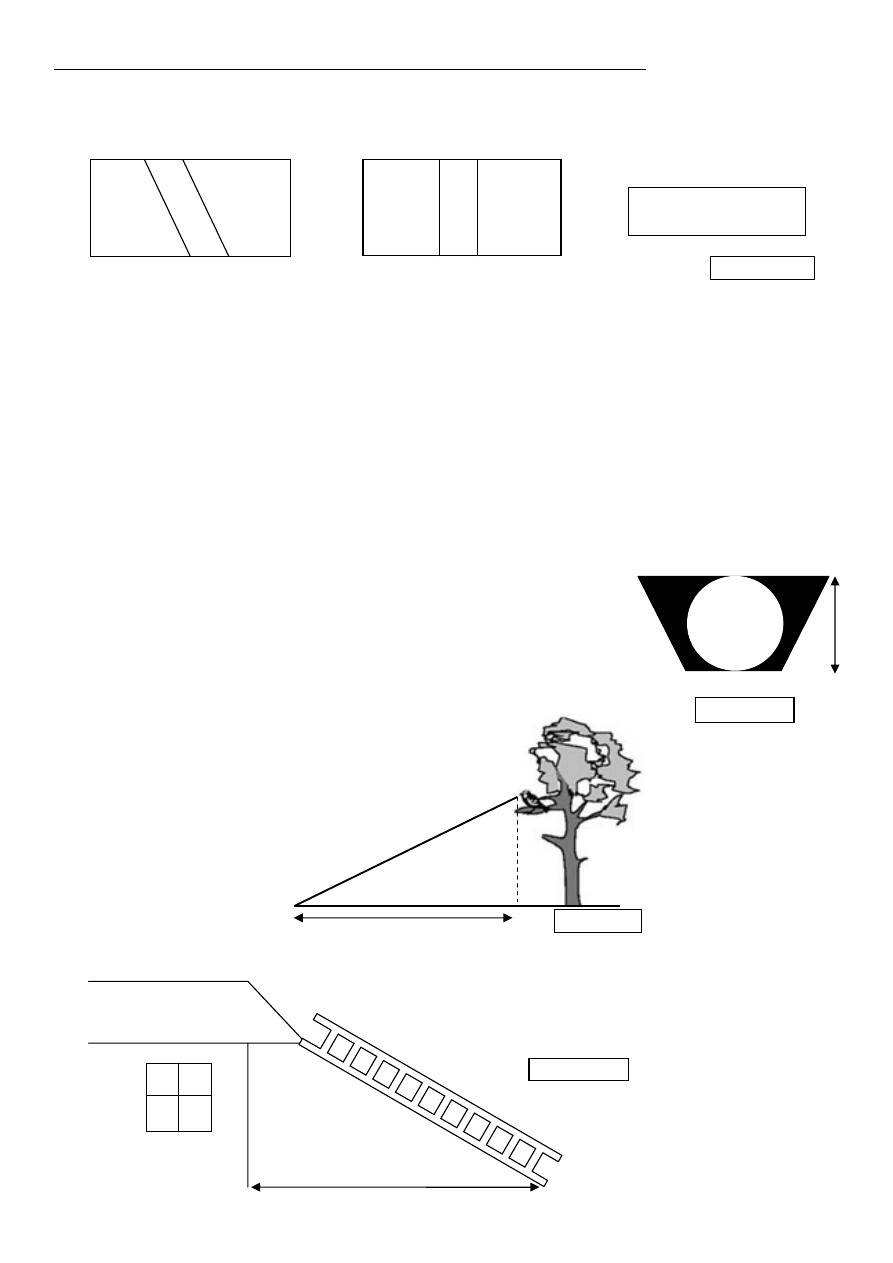
23. Perkoz spostrzegł ryb

ę

. Oblicz, korzystaj

ą

c z rysunku 8 odległo

ść

d, pomi

ę

dzy

ptakiem a ryb

ą

.

24. Oszacuj powierzchni

ę

bie

ż

ni stadionu oraz rzutni do rzutu oszczepem, przedstawionych na rysunkach 9 i 10.

25. Przed przyst

ą

pieniem do budowy latawca Janek rysuje jego model (rysunek 11). Model

ten przedstawiono na rysunku w skali 1:10. Oblicz pole powierzchni latawca
zbudowanego przez Janka, wiedz

ą

c,

ż

e długo

ś

ci odcinków AC i BD równe s

ą

odpowiednio 4 cm i 2 cm, oraz AC

⊥

BD i S –

ś

rodek BD. Zapisz obliczenia.

26. Oblicz wysoko

ść

drzewa na rysunku 12.

27. Na rysunku 13 przedstawiono tor jazdy narciarza. Oblicz, jak

ą

długo

ść

ma trasa

przejechana slalomem przez narciarza. Wynik podaj z dokładno

ś

ci

ą

do jedno

ś

ci.

28. Oblicz wysoko

ść

drzewa, na które wyszedł kot. Skorzystaj z pomiarów zilustrowanych

na rysunku 14.

8 m


8 m




7 m

12 m

Rysunek 6

2

8

m

7 m

Rysunek 7

8 m

6 m

d

Rysunek 8

Rysunek 9

10 m

100 m

60 m

80 m

40

°

Rysunek 10

Rysunek 12

8 m

60

°

800 m

400 m

200 m

Rysunek 13

Rysunek 14

18 m

30

°

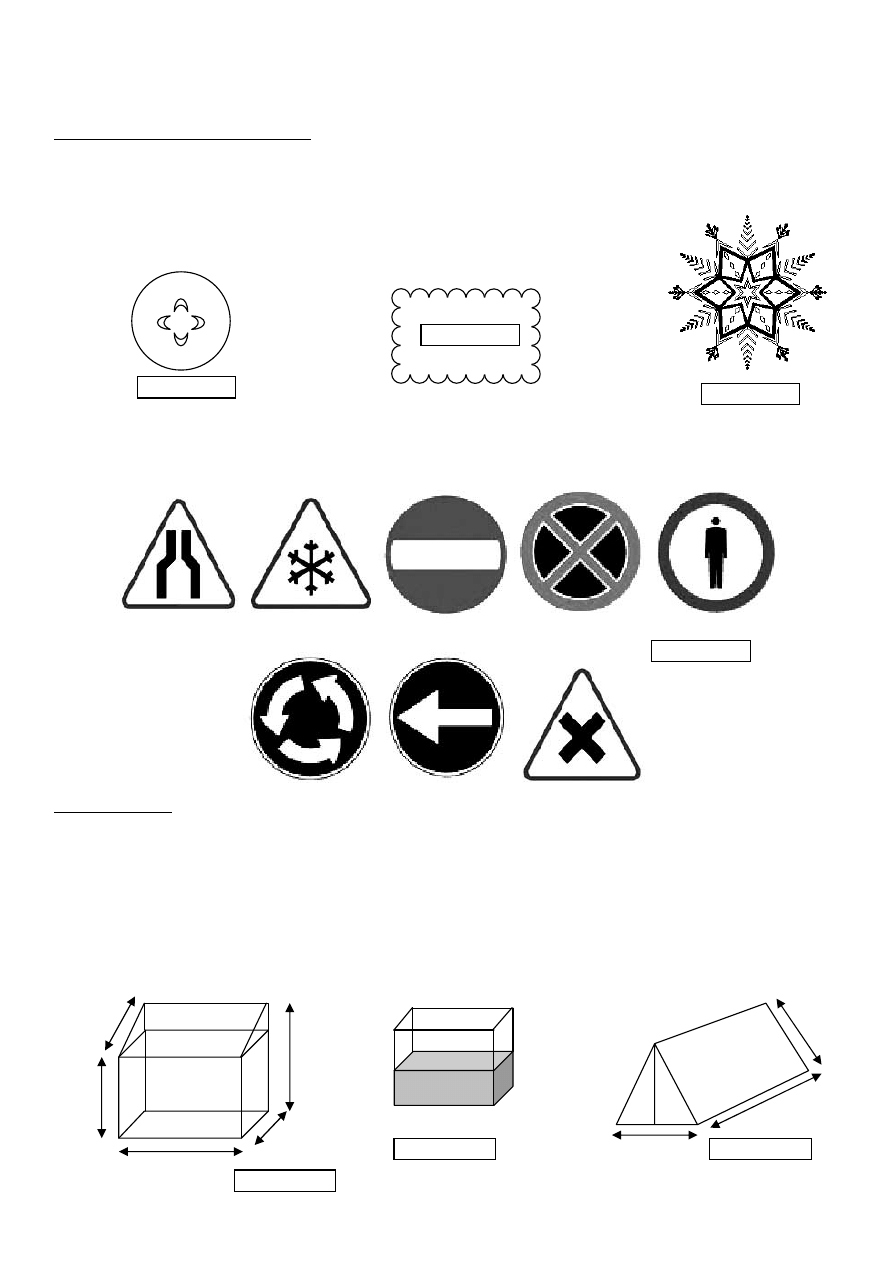
29. W parku na klombie rosn

ą

kwiaty. Klomb ma kształt trapezu równoramiennego, którego boki maj

ą

5 m, 4 m, 5 m i

10 m. Ile kwiatów ro

ś

nie na tej działce, je

ś

li na ka

ż

dym metrze kwadratowym posadzono po 35 kwiatów.

OSIE SYMETRII -

Ś

RODKI SYMETRII

30. Rysunek 15 przedstawia meduz

ę

chełbi modrej. Ile osi symetrii ma narysowana meduza?

31. Ile osi symetrii ma znaczek pocztowy na rysunku 16?

32. Ile osi symetrii ma płatek

ś

niegu przedstawiony na rysunku 17 ?

33. Narysuj osie symetrii (je

ś

li istniej

ą

) poszczególnych znaków drogowych. Który z poni

ż

szych znaków jest

ś

rodkowosymetryczny (rysunek 18)?

STEREOMETRIA

34. Na rysunku 19 przedstawiony jest schemat budowy karmnika dla ptaków. Oblicz, jak

ą

ł

ą

czn

ą

długo

ść

b

ę

d

ą

miały

listewki potrzebne do zbudowania kraw

ę

dzi tego karmnika.

35. Akwarium, w którym Marek hoduje rybki, ma wymiary 5 dm, 8 dm, 6 dm. Marek wlewa do niego wod

ę

przepływaj

ą

c

ą

przez kran z szybko

ś

ci

ą

8 dm

3

na minut

ę

. Do jakiej wysoko

ś

ci woda w akwarium b

ę

dzie si

ę

ga

ć

po

10 minutach (rysunek 20)?

36. Oblicz ile litrów powietrza mo

ż

e pomie

ś

ci

ć

namiot na rysunku 21. Wynik podaj w przybli

ż

eniu z dokładno

ś

ci

ą

do

jednego litra?

Rysunek 16

Rysunek 15

Rysunek 17

Rysunek 18

Rysunek 19

25 cm

30 cm

30 cm

20 cm

4

5

c

m

6 dm

5 dm

8 dm

Rysunek 20

1,2 m

2,5 m

1,2 m

Rysunek 21

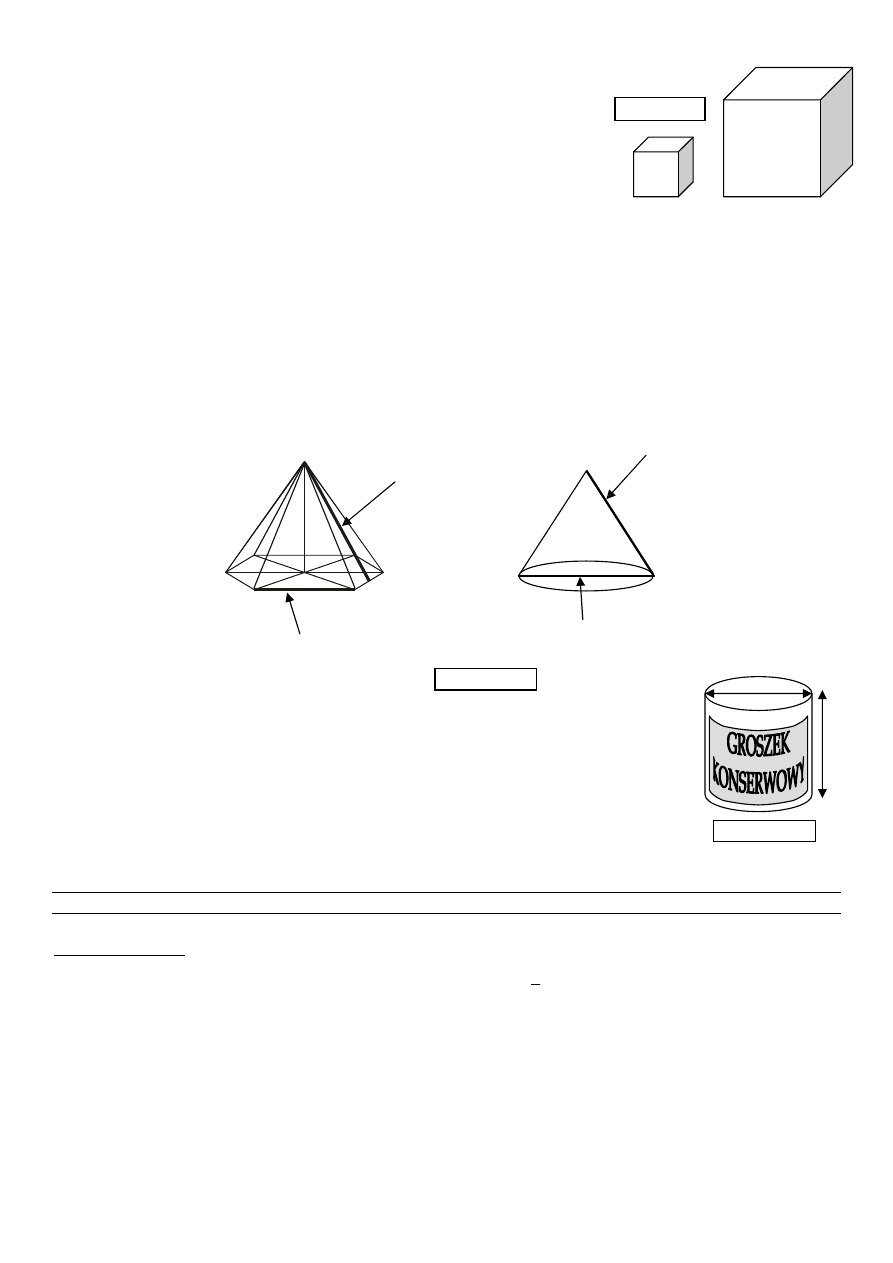
37. Do naczynia w kształcie prostopadło

ś

cianu o wymiarach: 3 dm; 1,5 dm i 1,2

dm, wypełnionego całkowicie wod

ą

, wło

ż

ono sze

ś

cienn

ą

ołowian

ą

kostk

ę

,

której pole powierzchni całkowitej jest równe 600 cm

2

. Oblicz, ile litrów wody

pozostało w naczyniu po wło

ż

eniu kostki. Pami

ę

taj o jednostkach.

38. Ile razy wi

ę

cej wa

ż

y wi

ę

ksza kostka sze

ś

cienna od małej na rysunku 22?

39. Jeden m

3

puszystego

ś

niegu wa

ż

y 0,1 t. Ile ton

ś

niegu trzeba usun

ąć

z

uliczki, której długo

ść

wynosi 250 m, szeroko

ść

10 m, a warstwa

ś

niegu ma

0,5 m grubo

ś

ci?

40. W czasie prac wykopaliskowych wydobyto 45 m

3

ziemi, z której usypano kopiec w kształcie sto

ż

ka. Jego pole

podstawy jest równe 54 m

2

. Oblicz wysoko

ść

kopca.

41. Podstaw

ą

piramidy egipskiej jest kwadrat o boku 40 m. Wysoko

ść

piramidy wynosi 30 m. Oblicz, ile ton kamieni

zu

ż

yto do budowy tej piramidy, je

ś

li głaz o obj

ę

to

ś

ci 1 m

3

wa

ż

y 800 kg?

42. Ile cm

3

obj

ę

to

ś

ci b

ę

dzie mie

ć

kulka z plasteliny o

ś

rednicy 6 cm?

43. Na zabaw

ę

karnawałow

ą

Beata wykonała kartonowe czapeczki w kształcie brył narysowanych poni

ż

ej (rysunek

23). Ile papieru zu

ż

yła na ka

ż

d

ą

z czapeczek? Na któr

ą

czapeczk

ę

zu

ż

yła wi

ę

cej papieru?

44. Jaka jest obj

ę

to

ść

puszki z groszkiem konserwowym (rysunek 24)? Wynik podaj

w przybli

ż

eniu z dokładno

ś

ci

ą

do mililitra.

ZADANIA PRAKTYCZNE – RÓWNANIA, NIERÓWNO

Ś

CI, UKŁADY RÓWNA

Ń

I INNE…

ZADANIA ZWYKŁE

1. Po przej

ś

ciu 3 km od miejsca startu Michał obliczył,

ż

e przebył ju

ż

3

2

drogi do obozu. Ile kilometrów wynosiła cała

droga?

2. Jad

ą

c w góry Jacek wzi

ą

ł ze sob

ą

110 złotych. Na lody wydał trzy razy wi

ę

cej ni

ż

na słodycze. Na napoje wydał o

10 złotych wi

ę

cej ni

ż

na słodycze. Na upominki wydał 15 złotych. Oblicz ile pieni

ę

dzy wydał na lody, je

ś

li do domu

przywiózł zaoszcz

ę

dzone podczas wycieczki 10 złotych?

3. W klasie uczy si

ę

26 uczniów. Chłopców jest o czterech wi

ę

cej ni

ż

dziewcz

ą

t. Ile jest w tej klasie dziewcz

ą

t, a ilu

chłopców?

4. Ania zebrała w albumie ł

ą

cznie 98 zdj

ęć

i widokówek z wakacji. Zdj

ęć

było o 42 wi

ę

cej ni

ż

widokówek. Ile było w

albumie zdj

ęć

, a ile widokówek?

5. Jacek i Paweł zbieraj

ą

znaczki. Jacek ma o 30 znaczków wi

ę

cej ni

ż

Paweł. Razem maj

ą

350 znaczków. Ile

znaczków ma Paweł?

Rysunek 22

6 cm

2 cm

Rysunek 23

30 cm - długo

ść

tworz

ą

cej

długo

ść

ś

rednicy 20 cm

30 cm - wysoko

ść

ś

ciany bocznej

10 cm - długo

ść

kraw

ę

dzi podstawy

w kształcie sze

ś

ciok

ą

ta foremnego

1

0

c

m

8 cm

Rysunek 24

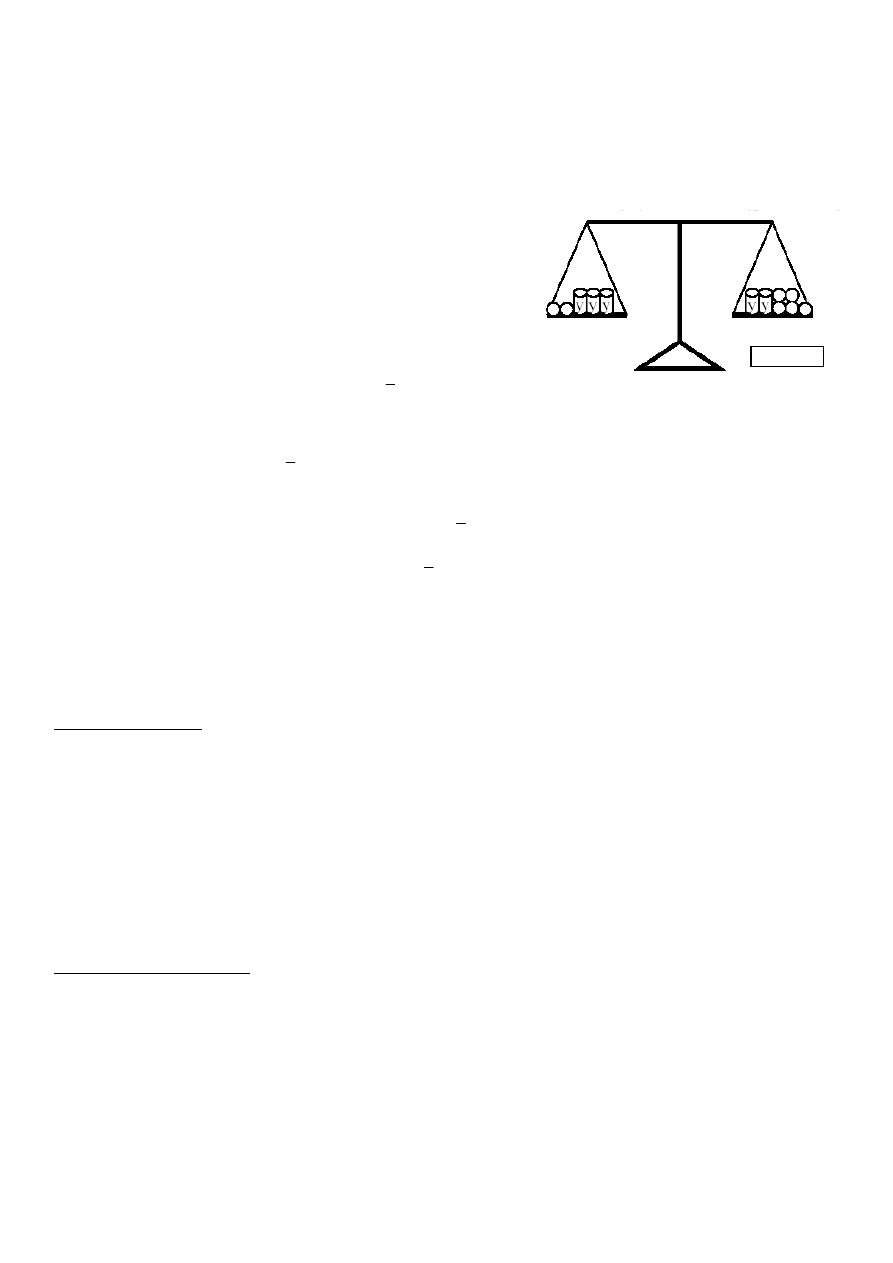
6. Paweł kupił australijski znaczek i 3 znaczki krajowe. Ka

ż

dy znaczek krajowy kosztował tyle samo. Za wszystkie

znaczki zapłacił 16 zł. Ile kosztował znaczek australijski, je

ś

li był pi

ę

ciokrotnie dro

ż

szy ni

ż

znaczek krajowy?

7. Za 5 bułek i jogurt zapłacono 3 złote 70 groszy, a za 3 bułki i dwa jogurty cena wyniosła 3 złote i 90 groszy. Ile

kosztuje bułka, a ile jogurt?

8. Do pracowni komputerowej zakupiono 8 nowych monitorów i 6 drukarek za ł

ą

czn

ą

kwot

ę

9400 zł. Drukarka była o

300 zł ta

ń

sza ni

ż

monitor. Oblicz cen

ę

monitora oraz drukarki.

9. W dwóch miastach mieszka w sumie około 300 tys. osób. W pierwszym z tych miast

ż

yje o około 36 tysi

ę

cy

wi

ę

cej osób ni

ż

w drugim. Oblicz ile mieszka

ń

ców liczy ka

ż

de

z tych miast?

10. W Białowieskim Parku Narodowym

ż

yj

ą

obecnie 542

ż

ubry,

przy czym po polskiej stronie jest ich o 88 mniej ni

ż

po

białoruskiej. Oblicz, ile

ż

ubrów

ż

yje po stronie polskiej?

11. Przypatrz si

ę

na rysunek 1 (obok) i znajd

ź

wag

ę

walca

wiedz

ą

c,

ż

e jest on ci

ęż

szy od kulki o 10 dag. Oznacz przez y

wag

ę

walca, a przez x – wag

ę

kulki.

12. Janek robił zakupy. Za jabłka zapłacił

5

1

posiadanych

pieni

ę

dzy, za mandarynki 2 złote wi

ę

cej, a za słodycze zapłacił dwa razy tyle co za jabłka. Po zapłaceniu

rachunku zostało mu 2 złote reszty. Oblicz, ile pieni

ę

dzy miał Jacek?

13. Marcin przebywa autobusem

4

3

drogi do jeziora, a pozostał

ą

cz

ęść

piechot

ą

. Oblicz odległo

ść

mi

ę

dzy domem

Marcina a jeziorem, je

ż

eli trasa, któr

ą

przebywa pieszo, jest o 8 km krótsza ni

ż

trasa, któr

ą

przebywa autobusem.

14. Darek jest o 20 kg ci

ęż

szy od Basi, a waga Basi wynosi

4

3

wagi Darka. Ile wa

ż

y Darek, a ile Basia?

15. W zawodach wzi

ę

li udział uczniowie klas trzecich.

4

1

wszystkich uczniów grała w piłk

ę

no

ż

n

ą

, natomiast co pi

ą

ty

ucze

ń

wzi

ą

ł udział w rozgrywkach siatkarskich. Pozostali uczniowie – w sumie 33 osoby – wzi

ę

li udział w

zawodach lekkoatletycznych. Ilu uczniów wzi

ę

ło udział w zawodach?

16. Krzy

ś

postanowił,

ż

e ze swojego kieszonkowego b

ę

dzie odkładał co tydzie

ń

15 złotych. Aby kupi

ć

desk

ę

snowboardow

ą

musiałby uzbiera

ć

co najmniej 470 złotych. Ile czasu trwałoby zebranie tej kwoty? Ile to miesi

ę

cy?

Czy jest to wi

ę

cej ni

ż

rok?

ZADANIA Z WIEKIEM

17. Piotr jest o cztery lata starszy od Kasi. Sze

ść

lat temu był od niej trzykrotnie starszy. Ile lat ma Piotr, a ile Kasia?

18. Maciek i Małgosia maj

ą

w sumie 18 lat. Za sze

ść

lat Maciek b

ę

dzie od Małgosi dwukrotnie starszy. Ile lat ma teraz

Maciek, a ile Małgosia?

19. Jacek jest o trzy lata starszy od Ani. Osiem lat temu był od niej dwukrotnie starszy. Ile lat ma Jacek a ile Ania?

20. Piotrek jest trzykrotnie starszy od Ani. Za pi

ęć

lat b

ę

dzie od niej dwukrotnie starszy. Ile lat ma teraz Piotrek, a ile

Ania?

21. Dwaj bracia – Bogdan i Adrian maj

ą

w sumie 16 lat. Gdyby Adrian urodził si

ę

rok pó

ź

niej byłby dwukrotnie

młodszy od brata. Oblicz, ile lat ma ka

ż

dy z chłopców?

ZADANIA GEOMETRYCZNE

22. W trójk

ą

cie prostok

ą

tnym ró

ż

nica miar dwu k

ą

tów ostrych wynosi 28°. Jakie miary maj

ą

k

ą

ty tego trójk

ą

ta?

23. W trójk

ą

cie równoramiennym ró

ż

nica dwóch k

ą

tów wynosi 32°. Oblicz miary tych k

ą

tów.

24. Jeden bok prostok

ą

ta jest pi

ę

ciokrotnie dłu

ż

szy od drugiego. Oblicz pole tego prostok

ą

ta wiedz

ą

c,

ż

e jego obwód

wynosi 48 cm.

25. Jeden bok prostok

ą

ta jest trzykrotnie dłu

ż

szy od drugiego. Oblicz pole tego prostok

ą

ta wiedz

ą

c,

ż

e jego obwód

wynosi 24 cm. W rozwi

ą

zaniu wykorzystaj odpowiedni układ równa

ń

.

26. Jedna podstawa trapezu ma 6 cm, a wysoko

ść

4 cm. Jaka powinna by

ć

długo

ść

drugiej podstawy, aby pole było

wi

ę

ksze ni

ż

18 cm

2

?

Rysunek 1

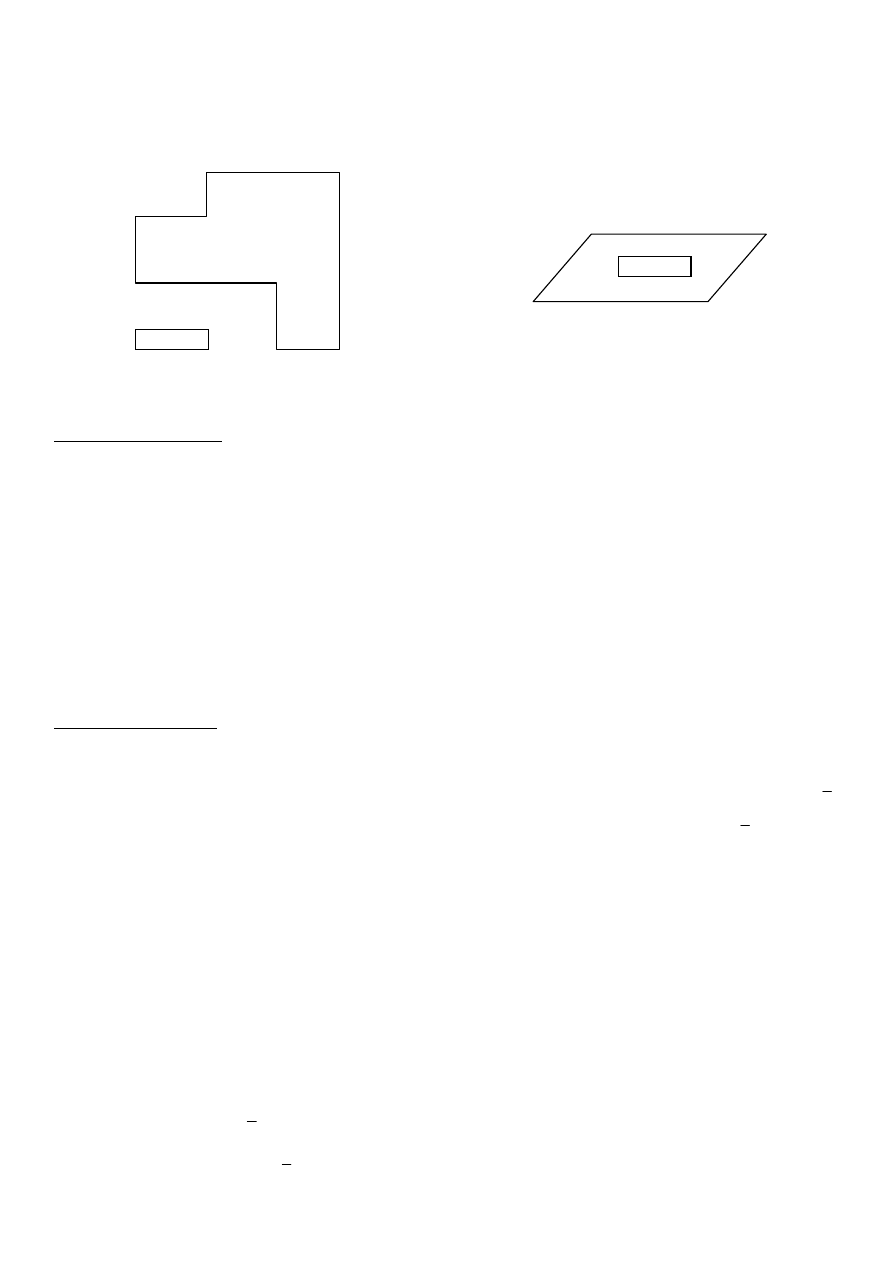
27. Odcinek podzielono w stosunku 3 : 2. Jak

ą

długo

ść

miał cały odcinek, je

ś

li jedna cz

ęść

jest o 8 cm dłu

ż

sza od

drugiej?

28. Znajd

ź

obwód równoległoboku przedstawionego na rysunku 2.

29. Oblicz długo

ść

boku x wiedz

ą

c,

ż

e obwód narysowanej figury (rysunek 3) wynosi 44 cm.

PROPORCJONALNO

ŚĆ

30. Na pomalowanie 4 m

2

ś

ciany potrzeba 0,5 litra farby. Czy wystarczy puszka farby o pojemno

ś

ci 2 litrów na

pomalowanie powierzchni

ś

ciany o wymiarach 6 m i 2,5 m?

31. Samochód jad

ą

c ze stał

ą

pr

ę

dko

ś

ci

ą

80 km/h pokona tras

ę

w 1,5 h. Ile czasu wyniesie czas przejazdu tej samej

trasy samochodem jad

ą

cym z pr

ę

dko

ś

ci

ą

ś

redni

ą

równ

ą

50 km/h (wynik podaj w minutach).

32. Aby napełni

ć

akwarium o pojemno

ś

ci 60 litrów nale

ż

y nalewa

ć

wod

ę

przez 4 minuty. Jak długo napełnialiby

ś

my

wann

ę

o obj

ę

to

ś

ci 370 litrów, je

ś

li przepływ wody byłby taki sam jak podczas napełniania akwarium?

33. Wyprodukowany napój nale

ż

y rozla

ć

do butelek. Je

ś

li producent zdecydowałby si

ę

na sprzeda

ż

napoju w

butelkach dwulitrowych, to musiałby ich przygotowa

ć

450. Oblicz, ile potrzebowałby butelek o obj

ę

to

ś

ci 1,5 litra,

gdyby zdecydował si

ę

na tak

ą

form

ę

sprzeda

ż

y?

34. Za 4,6 kg wołowiny nale

ż

y zapłaci

ć

w hurtowni 26 złotych i 80 groszy. Ile mi

ę

sa wołowego mo

ż

na byłoby kupi

ć

za

100 złotych?

ODSZUKIWANIE LICZB

35. Znajd

ź

liczb

ę

wiedz

ą

c,

ż

e jest ona mniejsza o 22 od swojej trzeciej wielokrotno

ś

ci.

36. Gdyby do licznika i mianownika pewnego ułamka doda

ć

liczb

ę

2, to po skróceniu otrzymaliby

ś

my liczb

ę

5

1

.

Dodaj

ą

c do licznika i mianownika szukanego ułamka liczb

ę

1, otrzymaliby

ś

my po skróceniu

6

1

. Znajd

ź

ten

ułamek.

37. Jedna liczba jest o 5,6 wi

ę

ksza od drugiej. Znajd

ź

te liczby, je

ś

li ich suma wynosi 10,1.

38. Suma cyfr liczby dwucyfrowej wynosi 10. Gdy w liczbie tej przestawimy cyfry to otrzymamy liczb

ę

o 18 wi

ę

ksz

ą

.

Znajd

ź

t

ę

liczb

ę

.

39. Suma cyfr liczby dwucyfrowej wynosi 6. Gdy w liczbie tej przestawimy cyfry to otrzymamy liczb

ę

o 36 mniejsz

ą

.

Znajd

ź

t

ę

liczb

ę

. W rozwi

ą

zaniu wykorzystaj odpowiedni układ równa

ń

.

40. Małgosia dostała w tym półroczu nast

ę

puj

ą

ce oceny z matematyki: dwie dopuszczaj

ą

ce, jedn

ą

dostateczn

ą

i

jedn

ą

ocen

ę

dobr

ą

. Oblicz, ile powinna otrzyma

ć

ocen bardzo dobrych, aby

ś

rednia arytmetyczna ocen z

matematyki wynosiła co najmniej 4?

41. W pewnej liczbie trzycyfrowej suma cyfr wynosi 17. Cyfra jedno

ś

ci jest trzy razy wi

ę

ksza od cyfry setek, natomiast

cyfra dziesi

ą

tek jest o 2 wi

ę

ksza od cyfry setek. Znajd

ź

t

ą

liczb

ę

.

42. Felek Korniszon urodził si

ę

XX wieku. Znajd

ź

rok urodzin Felka wiedz

ą

c,

ż

e suma cyfr roku urodzenia wynosi 20,

a cyfra jedno

ś

ci stanowi

4

1

cyfry dziesi

ą

tek.

43. Stosunek dwóch liczb wynosi

3

1

, a ich ró

ż

nica wynosi 16. Ile wynosi iloczyn tych liczb?

44.

Ś

rednia arytmetyczna liczb n i k wynosi 4,5, a ich ró

ż

nica wynosi 13. Znajd

ź

te liczby.

x + 3

2y - 3

x - 1

3y - 5

Rysunek 3

Rysunek 2

4 cm

4 cm

10 cm

x

ZADANIA RÓ

ś

NE

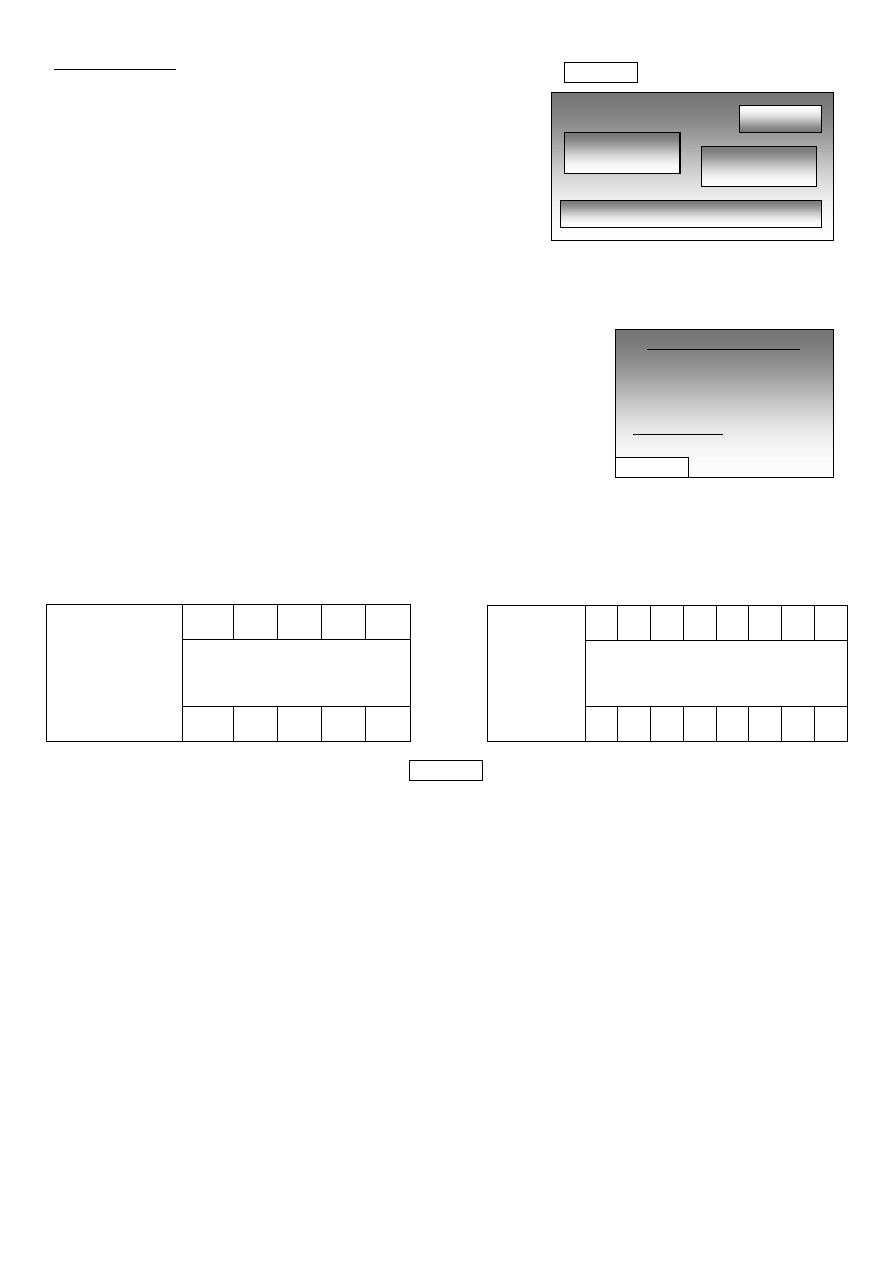
45. Przypatrz si

ę

na informacje zawarte na bilecie (rysunek 4) i oblicz,

ile wynosi

ś

redni koszt przejechania 100 km na trasie z Gdyni do

Warszawy.

46. Przez rezerwat le

ś

no - wydmowy w Słowi

ń

skim Parku Narodowym

prowadz

ą

cztery szlaki turystyczne z Rowów do Łeby. Na ile

sposobów turysta mo

ż

e zaplanowa

ć

wycieczk

ę

na trasie Rowy -

Łeba - Rowy, je

ś

li z Łeby do Rowów nie chce wraca

ć

tym samym

szlakiem, którym szedł z Rowów do Łeby?

47. Maciek z rodzicami planuje wakacyjny wyjazd. Biuro podró

ż

y oferuje 14-dniowy pobyt na Mazurach dla 3-

osobowej rodziny w cenie 2100 zł (noclegi + wy

ż

ywienie). Za 16-dniowe wczasy 3-osobowej rodziny w

Zakopanem trzeba zapłaci

ć

2775 zł, przy czym 12% tej kwoty stanowi

ą

koszty dojazdu. Oblicz, ile trzeba zapłaci

ć

za ka

ż

dy dzie

ń

pobytu jednej osoby na Mazurach, a ile w Zakopanem. Wynik zaokr

ą

glij do pełnych złotych.

48. Stosunek ceny biletu kolejowego pierwszej klasy do ceny biletu drugiej klasy

wynosi 3:2. O ile złotych dro

ż

szy byłby bilet pierwszej klasy od biletu drugiej

klasy, za który nale

ż

y zapłaci

ć

17,50 PLN?

49. Uczniowie zaplanowali wycieczk

ę

kolejk

ą

linow

ą

. Postanowili,

ż

e wyjad

ą

autobusem mi

ę

dzy 8

00

a 10

00

. Andrzej miał ustali

ć

, o której godzinie powinni

wyjecha

ć

, aby na stacji kolejki nie czeka

ć

dłu

ż

ej ni

ż

10 min. Czas przejazdu

autobusu wynosi 22 min. Jak

ą

godzin

ę

wyjazdu powinien Andrzej

zaproponowa

ć

kolegom (skorzystaj z informacji na rysunku 5)?

50. Narciarz ma do wyboru dwa rodzaje karnetów: M uprawniaj

ą

cy do 10

wjazdów i D uprawniaj

ą

cy do 16 wjazdów. Oblicz, jaki jest koszt jednego przejazdu narciarza, który zakupił karnet

M, a jaki jest koszt jednego przejazdu narciarza, który zakupił karnet D? Kto płaci wi

ę

cej za jeden przejazd i ile

wynosi ró

ż

nica w cenie (skorzystaj z informacji zawartych na rysunku 6)?

KARNET

M

1

2

3

4

5

Wyci

ą

g krzesełkowy „Baca”

Cena: 26 zł

10

9

8

7

6

KARNET

D

1

2

3

4

5

6

7

8

Wyci

ą

g krzesełkowy „Baca”

Cena: 40 zł

1
6

1
5

1
4

1
3

1
2

1
1

1
0

9

Od Gdynia Główna do Warszawa Centralna

KLASA 1

Odległo

ść

: 350 km

Cena: 53,18 PLN

BILET – POCI

Ą

G

EKSPRESOWY

Rysunek 4

Rysunek 6

Rozkład jazdy autobusów:

6.02, 6.40, 7.07, 7.47, 8.14, 8.54,

9.01, 9.39, 10.46, 11.53, 12.00,

13.07, 14.14, 14.52, 15.21,15.59
16.06, 16.44, 17.13, 18.20,19.27

Odjazdy kolejki

od 7.00 do 16.00

co pół godziny

Rysunek 5