dr Anna Barbaszewska-Wiśniowska

ZAGADNIENIA Z MATEMATYKI DLA STUDENTÓW I ROKU WIMiR

Semestr letni 2012/2013

1. Liczby zespolone - cztery postacie. Moduł, argument, sprzężenie - definicje i własności. Interpretacja geometryczna.

2. Własności działań na liczbach zespolonych.

3. Potęgowanie liczb zespolonych. Wzór de Moivre'a. Zastosowanie do wyprowadzenia wzorów na
   .

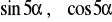
4. Pierwiastkowanie. Różne sposoby obliczania pierwiastków.

5. Obliczenie
   ,
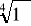
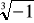
   - różnymi sposobami.

6. Rozwiązywanie równań w dziedzinie zespolonej.

7. Ogólne pojęcie metryki, kula, sfera

8. Metryka zespolona. Zastosowanie do interpretacji graficznej równań i nierówności z modułem.

9. Działania na macierzach.

10. Macierz odwrotna. Definicja. Rózne sposoby obliczania.

11. Równania macierzowe. Przykład.

12. Układy równań liniowych jednorodnych i niejednorodnych - postać macierzowa układu.

13. Tw. Kroneckera-Capellego.

14. Tw. Cramera.

15. Własności układów jednorodnych.

16. Interpretacja geometryczna w
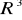
    pewnych układów - wzajemne położenie płaszczyzn.

17. Równanie płaszczyzny w
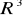
    - wyprowadzenie. Postacie.

18. Równanie prostej w
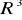
    - wyprowadzenie. Postacie.

19. Rzuty na prostą i płaszczyznę.

20. Elementy przestrzeni wektorowej. Liniowa niezależność, baza, ogólny iloczyn skalarany.

21. Odwzorowanie liniowe. Macierz odwzorowania. Rownania liniowe w przestrzeniach wektorowych.

22. Funkcje wielu zmiennych - dziedzina, wykres, zbiór wartości, warstwica, granice i ciągłość - zastosowanie współrzędnych biegunowych. Przykłady.

23. Pochodne cząstkowe pierwszego i wyższych rzędów. Twierdzenie o pochodnych mieszanych. Przykłady.

24. Pochodne kierunkowe: definicja, związek z gradientem, przykład obliczania.

25. Twierdzenie o postaci różniczki, wartość różniczki na i-tym wersorze bazy kanonicznej. Gradient - związek z różniczką. Przykład.

26. Różniczka drugiego rzędu, macierz Hessego, określoność dodatnia i ujemna, półokreśloność - dla funkcji dwóch, trzech i większej liczby zmiennych. Przykłady.

27. Warunek konieczny istnienia ekstremum funkcji wielu zmiennych. Przykład, że nie jest to warunek wystarczający.

28. Warunek wystarczający istnienia ekstremum funkcji wielu zmiennych. Przykłady.

29. Zastosowanie różniczek do obliczeń przybliżonych.

30. Płaszczyzna styczna i prosta normalna do powierzchni w
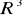
    i przypadek szczególny kiedy powierzchnia jest wykresem funkcji dwóch zmiennych - analogia do wzoru na prostą styczną do wykresu dla funkcji jednej zmiennej

31. Wyjaśnij pojęcia: całka ogólna równania różniczkowego, całka szczególna równania różniczkowego, rozwiązanie explicite, rozwiązanie implicite, całka syngularna, krzywa całkowa.

32. Wymień wszystkie poznane typy równań różniczkowych, podaj ich postać ogólną i zilustruj dwoma przykładami.

33. Równanie rozpadu promieniotwórczego. Wyprowadzenie wzoru na
    .

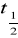
34. Równania różniczkowe o zmiennych rozdzielonych i równania do nich sprowadzalne.

35. Cztery równania „indywidualne”. Omówienie szczegółowe dwu przypadków.

36. Równania różniczkowe liniowe rzędu I (lj, lnj) - tw. O postaci rozwiązania.

37. Tw. o postaci rozwiązania równania różniczkowego lnj rzędu II.

38. Równania różniczkowe lj rzędu II o stałych współczynnikach - sposoby znajdowania dwu całek szczególnych l.n. w trzech przypadkach. Uogólnienie sytuacji dla równań wyższych rzedów.

39. Porównaj (wskaż podobieństwa i różnice) metody wariacji stałych dla równań rzędu I oraz rzędu II.

40. Metoda przewidywań.

41. Metoda wariacji stałych dla równań II rzędu.

42. Zastosowanie liczb zespolonych w rozwiązywaniu równań różniczkowych

43. Zastosowanie twierdzenia Cramera do rozwiązywania równań różniczkowych

44. Elipsa - podejście geometryczne, analityczne (kartezjańskie, parametryczne, różniczkowe, zespolone).

45. Okrąg, jako szczególny przypadek elipsy. Równania różniczkowe rodziny okręgów

46. Całka oznaczona Riemana. Definicja, własności. Tw. Newtona-Leibnitza. (z I semestru)

47. Całka niewłaściwa. Definicja. Przykłady zastosowań do obliczania pól figur nieskończonych. Przykłady całek zbieżnych i rozbieżnych. (z I semestru)

48. Całka podwójna - analogie i różnice z całką Riemana (pojedynczą). Interpretacja geometryczna.

49. Twierdzenie o całkowaniu w obszarach normalnych, całki iterowane - dwa przykłady.

50. Kiedy i jak możemy dokonać zmiany kolejności całkowania? Dwa przykłady.

51. Pole powierzchni figury płaskiej - obliczanie z zastosowaniem całki pojedynczej i podwójnej. Uzasadnienie wzoru z wykorzystaniem całki podwójnej.

52. Przykłady obliczania objętości bryły za pomocą całki podwójnej. Dla jakich brył możemy użyć całki pojedynczej.

53. Twierdzenie o zmianie zmiennych w całce podwójnej (jakobian przekształcenia z R2 → R2 - związek z odpow. twierdzeniem dla całki pojedynczej. Przykłady.

---