Kulawik Bartosz
Gr. 23 IIID

Analiza i Identyfikacja Sygnałów
Sprawozdanie - laboratorium 1

1. Ćwiczenie 1
   Układ równań: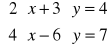
   

1. Rozwiąż numerycznie podany układ równań
   A=[2 3; 4 -6];

B=[4; 7];

X=A\B
X =

1.8750

0.0833

2. Rozwiąż graficznie podany układ równań
   
   
   x=-10:0.01:10;
   y1=(4-2*x)/3;
   y2=(-7+4*x)/4;
   plot(x,y1,'r',x,y2,'k',X(1),X(2),'o')
   title('Solution of system equations')
   xlabel('X')
   ylabel('Y')
   text(X(1)+1,X(2)+0.6,'Solution: ')
   text(X(1)+1,X(2)-0.6,'point [1.8750 0.0833]')
   text(-4,5,'2x+3y=4')
   text(-4,-6.5,'4x-6y=7')
   
   

2. Ćwiczenie 2
   Mając dane równanie: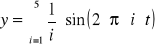
   
   Narysuj wykres funkcji i wykonaj opis rysunku
   dt=1/500;
   t=0:dt:4;
   for i=1:5
   y1=(1/i)*sin(2*pi*i*t);
   y=y+y1;
   end
   plot(t,y,'g')
   grid on
   title('Suma pieciu funkcji sinusoidalnych')
   xlabel('czas[sec]')
   ylabel('y(t)')
   
   
   
   
   
   

3. Ćwiczenie 3
   Dla danego równania: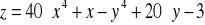
   wykonać trójwymiarowy wykres przebiegu funkcji i wykonać opis rysunku
   [x,y]=meshgrid(-2:0.1:2,-5:0.1:5);
   z=40.*x.^4+x-y.^4+20.*y-3;
   mesh(x,y,z);
   title('Wykres funkcji z = 40 × x^4 + x - y^4 + 20 × y - 3')
   xlabel('os X')
   ylabel('os Y')
   zlabel('os Z')
   
   
   
   
   
   

4. Ćwiczenie 4
   W przyborniku SIMULINK wygenerować sygnały umożliwiające wykreślenie krzywych lissajaus.
   
   
   
   
   

---