Jeśli oznaczymy
Pomoc dydaktyczna
Temat: Objętość graniastosłupa.
Klasa: V
Forma: Praca w grupach
Opracowanie:
Dorota Czech - Gimnazjum nr 2 we Wrześni
Magdalena Janowska - Szkoła Podstawowa nr 1 w Owińskach
Małgorzata Kaminiak - Szkoła Podstawowa nr 23 w Poznaniu
Anna Lankiewicz - Samorządowa Szkoła Podstawowa w Chociczy Wielkiej
Dorota Maciejewska - Gimnazjum w Jerzykowie.
Opis materiału:
Wprowadzenie pojęcia objętości graniastosłupa w oparciu o czynnościowe nauczanie matematyki. Zadania prowokujące czynności konkretne, wyobrażone i abstrakcyjne.
Materiał wypracowany w ramach kursu „Animacja na lekcjach matematyki”.
OBJĘTOŚĆ GRANIASTOSŁUPA
ZADANIA PROWOKUJACE CZYNNOŚCI KONKRETNE
Nauczyciel dysponuje identycznymi sześcianami oraz różnymi pudełkami w kształcie prostopadłościanu.
Zadanie 1. (zadanie może być wykonywane w grupach - każda grupa ma pudełko o innych wymiarach)
Wypełnijcie pudełko leżące na waszym stole kostkami (na ławkach uczniowie mają przygotowane w/w sześciany). Następnie wysypcie kostki i policzcie ile ich zmieściło się w pudełku.
N.: - Co w ten sposób zmierzyliśmy?
U.: Może paść odpowiedź - pojemność lub objętość.
N.: - Ilość kostek w każdym pudełku to jego objętość.
Zadanie 2. (zadanie może być wykonywane w grupach - każda grupa otrzymuje model prostopadłościanu i jednostkowe sześcianiki)
Ułóżcie z kostek prostopadłościan identyczny z wzorcowym. Ile kostek zużyliście budując swoją bryłę?
N.: Czy można je policzyć bez rozkładania ułożonej bryły?
U.: Tak. Trzeba pomnożyć ilość kostek w jednej warstwie przez ilość warstw.
N.: Jak obliczyć ilość kostek w jednej warstwie?
U.: Mnożymy długość przez szerokość podstawy.
Zapis w zeszycie.
Jeśli oznaczymy
H
b
a
![]()
objętość długość szerokość wysokość
bryły podstawy podstawy prostopadłościanu
Nauczyciel dysponuje modelem prostopadłościanu o wymiarach a, b i H oraz modelem graniastosłupa, którego podstawą jest trójkąt prostokątny o przyprostokątnych a i b, a wysokość graniastosłupa jest identyczna z wysokością prostopadłościanu. Obie bryły przystosowane są do wypełniana np. piaskiem.
Zadanie 3. ( zadanie wykonuje jeden uczeń)
Wypełnij graniastosłup trójkątny piaskiem. Przesyp zawartość do prostopadłościanu. Powtórz tę czynność jeszcze raz.
Jaką częścią objętości prostopadłościanu jest objętość danego graniastosłupa?
Uzupełnij zapis ;
VG = ……..![]()
VP = …….![]()
Pole podstawy
VG = …..![]()
Pole podstawy
Wniosek (zapisuje uczeń)
![]()
objętość pole wysokość
graniastosłupa podstawy graniastosłupa
ZADANIA PROWOKUJĄCE CZYNNOŚCI WYOBRAŻONE
Zadanie 1.
Oblicz objętość sześcianu o krawędzi 1 cm.
U.: 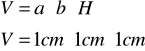
V = 1cm3 - jednostka objętości
Zadanie 2.
Oblicz objętości graniastosłupów prostych:
a)
10cm
6cm
5cm
b)
15cm podstawa
4cm
4cm
8cm
ZADANIA PROWOKUJĄCE CZYNNOŚCI ABSTRAKCYJNE
Zadanie 1.
Oblicz objętość graniastosłupa, którego podstawa jest rombem o przekątnych 8cm i 12 cm, a wysokość graniastosłupa ma długość 20cm.
Zadanie 2.
Oblicz ilość powietrza w sali, w której się znajdujesz.
Zadanie 3.
Objętość graniastosłupa prawidłowego czworokątnego wynosi 80cm3. Jaka jest długość krawędzi podstawy, jeśli wysokość graniastosłupa ma 5cm?
Zadanie 4.
Ile razy zwiększy się objętość graniastosłupa, jeśli podstawa będzie tą samą figurą geometryczną, a wysokość bryły zwiększymy trzykrotnie?
3
Opracowanie: Dorota Czech - Gimnazjum nr 2 we Wrześni
Magdalena Janowska - Szkoła Podstawowa nr 1 w Owińskach
Małgorzata Kaminiak - Szkoła Podstawowa nr 23 w Poznaniu
Anna Lankiewicz - Samorządowa Szkoła Podstawowa w Chociczy Wielkiej
Dorota Maciejewska - Gimnazjum w Jerzykowie