1. Prawo Kirchhoffa wyraża równanie:

Δ_rH'(T₂)= Δ_rH'(T₁)+
Δ_rC'_p dT (1)

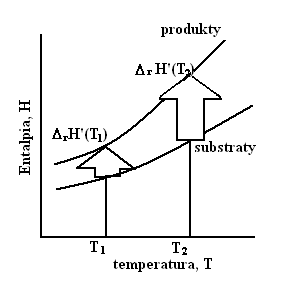
Rys. 1

Graficzne przedstawienie prawa Kirchhoffa

Δ_rH'(T₂) - standardowa entalpia reakcji w temperaturze T₂(szukana przez Nas)[kJ/mol]

Δ_rH'(T₁) - standardowa entalpia reakcji w temperaturze T₁(jest nam znana)[kJ/mol]

T - temperatura, [K]

Δ_rC'_p - różnica pomiędzy molowymi pojemnościami cieplnymi produktów i substratów w warunkach standardowych z uwzględnieniem ich współczynników stechiometrycznych[J/K*mol]

Δ_rC'_p =  _jC_p,m -  _iC_p,m (1.a)

^{produkty substraty}

 - współczynniki stechiometryczne

Prawo Kirchhoffa wykorzystujemy do obliczenia standardowej entalpii reakcji w interesującej Nas temp. na podstawie znajomości standardowej entalpii reakcji w innej temp. oraz pojemności cieplnych produktów i substratów w tym zakresie temperatur.

1. Definicje wielkości występujących we wzorze

Entalpia(H) - jest funkcją stanu(tzn. jej zmiana nie zależy od drogi przemiany) zdefiniowana jako:

h=u+pv (2)

Gdzie: u - energia wewnętrzna układu [J]

p - ciśnienie w układzie [N/m²]

v  objętość ogólna układu [m³]

gdy p=const i układ nie wykonuje pracy nieobjętościowej :

dh=dq (3)

Funkcje zwaną Entalpią wprowadzamy, gdy układ może wykonać pracę zmiany objętości. W takich warunkach część energii dostarczonej do układu na sposób ciepła wraca do otoczenia więc: du<dq

Dostarczone ciepło w takich warunkach jest równe zmianie Entalpii, czyli:

dh=dq przy p=const i gdy układ nie wykonuje pracy nieobjętościowej.

Dla wielkości mierzalnych:

Δh=q_p , q_p - ciepło mierzone pod stałym ciśnieniem (4)

Pojemność cieplna (C_p) przy p=const jest zdefiniowana :

C_p=(∂H/∂T)_p (5)

H-entalpia

T-temperatura[K]

Nachylenie wykresu entalpii jako funkcji temperatury, gdy p=const nazywamy Pojemnością cieplna pod stałym ciśnieniem(Rys.2)

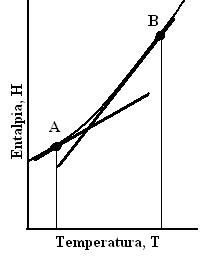
Rys. 2

Wykres pojemności cieplnej pod stałym ciśnieniem(linia gruba). Pojemność cieplna zależy od temperatury, dlatego jak to widać na wykresie pojemności w punktach A i B są różne.

Pojemność cieplna układu pod stałym ciśnieniem jest zmianą Entalpii układu w procesie izobarycznym odniesiona do zmiany temperatury układu w tym procesie.

Pojemność cieplna zależy od temperatury i w niskiej maleje. Dla niewielkich zakresów temp.(temp. pokojowa i wyższa)w przybliżonych obliczeniach przyjmujemy że jest niezależna od temperatury.

2. Wyprowadzenie Prawa Kirchhoffa:

Za pomocą wzoru nr (5) wiążemy zmianę Entalpii ze zmianą temperatury.

Dla nieskończenie małych zmian temperatury.

dH=C_pdT (6)

całkując w granicach T₁ - T₂ (zakres temperatur w których ogrzewamy substancje), otrzymujemy:

H(T₂)=H(T₁) +
C_p dT (7)

(zakładamy ze w temperaturze ot T₁ do T₂ nie zachodzą przemiany fazowe)

Równanie jest słuszne dla każdego z reagentów, wiec standardowa entalpia reakcji zmienia się od temperatury T₁ do T₂ tak jak wyraża to równanie Kirchhoffa (1)

Entalpia standardowa reakcji Δ_rH' - jest zmianą Entalpii, w której substraty w swoich stanach standardowych ulegają przemianie w produkty w stanie standardowym. Jest ona ściśle powiązana z równaniem stechiometrycznym:

Δ_rH'=ΣυH'_m - ΣυH'_m

υ-współczynniki stechiometryczne

H'_m-standardowe entalpie produktów produktów substratów

Stan standardowy- substancji w danej temp. odpowiada jej czystej postaci pod ciśnieniem 1bar (temp. jest dowolna)

3. Zastosowanie prawa Kirchhoffa:

Standardowa entalpia tworzenia H₂O(c) w temp.298K wynosi -285,83 kJ/mol.Oblicz tę wielkość w temp.363K.

OBLICZENIA: korzystamy z prawa Kirchhoffa:

Δ_rH'(T₂)= Δ_rH'(T₁)+
Δ_rC'_p dT

Występuje tu Δ_rC'_p wyrażona równaniem 1.a

Równanie reakcji chemicznej to: H₂ + 1/2O₂= H₂O

Współczynniki stechiometryczne:ν(H₂)=1

ν(O₂)=1/2O₂

ν(H₂O)=1

dla naszego przypadku równanie 1.a przyjmuje więc postać:

Δ_rC'_p= C'_p,m(H₂O,c)-{C'_p,m(H₂,g)+1/2C'_p,m(O₂,g)} (8)

Molowa pojemność cieplna produktów i substratów zależy od temp. Więc korzystamy z przybliżonego wzoru empirycznego :

C'_p,m= a + bT + c/T²[J/mol*K] (9)

Gdzie a,b,c-parametry doświadczalne niezależne od temperatury,niektóre ich wartości podano w tabeli nr 1.

	a	b/(10^-3 K^-1)	c/(10^5 K^2)
C (s)	16.86	4.77	-8.54
CO2 (g)	44.22	8.79	-8.62
H2O (c)	75.29	0	0
N2 (g)	28.58	3.77	-0.5
H2 (g)	27.28	3.26	0.5
O2	29.96	4.18	-1.67

Podstawiając do wyrażenia (8) równanie nr (9) otrzymujemy całkę:

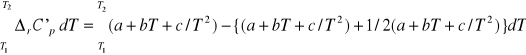
Całkę sumy możemy przedstawić jako sumę całek i liczyć poklei.Każda z tych całek jest taka sama więc całkując w granicach T₁ T₂ jedną z nich otrzymujemy wyrażenie ogólne:

Całka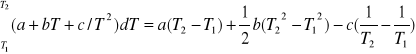
(10)

Dla (H₂O,c) C'_p,m po podstawieniu wartości liczbowych odpowiednich a,b,c do wyrażenia(10) otrzymujemy:

C'_p,m(H₂O,c)= 4893,85 [J/mol]

Podobnie postępujemy dla H₂ i O₂ podstawiając wartości a,b,c z tabelii 1 odpowiednie dla H₂ i O₂ do równania(10)otrzymując wartości molowych pojemności cieplnych w zakresie temp.298-363K dla tych substancji :

C'_p,m(H₂ ,g)= 1873,23 [J/mol]

C'_p,m(O₂ ,g)= 1936,99 [J/mol]

Z tego obliczamy :Δ_rC'_p=

Δ_rC'_p=2052,13 [J/mol]

Ostatecznie więc po podstawieniu danych liczbowych do równania(1)Δ_rH'(363K) wynosi:

Δ_rH'(363K)= -285,83 +2,052= -283,78 [kJ/mol]

Odp. Entalpia tworzenia H₂O w stanie ciekłym w temp.363K wynosi -283,78 [kJ/mol].

W przypadku gdy możemy założyć niezależność pojemności cieplnej od temp. W danym zakresie temp. korzystamu z ogólnego prawa Kirchhoffa wyrażonego wzorem

Δ_rH'(T₂)= Δ_rH'(T₁) +(T₂-T₁)Δ_rC'_p (11)

Jednak w takim przypadku uzyskujemy wyniki bardzo niedokładne.

4. Załącznik.

Temperatura(T)- definiowana jako parametr określający kierunek przepływu energii na sposób ciepła. Jeśli energia przepływa od ciała A do B stwierdzamy że ciało A ma wyższą temperaturę niż B. [K]

Energia wewnętrzna(u)- suma całkowitej energii kinetycznej i potencjalnej cząsteczek tworzących układ. [J]

Jest funkcją stanu zależy jedynie od aktualnego stanu układu a nie od drogi na jakiej ten stan został osiągnięty.

Nie można mierzyć U tylko jej zmianę, która jest różnicą energii wewnętrznej układu w stanie końcowym i początkowym:

Δu=u_k-u_p

W ogólnym przypadku zmiana energii wewnętrznej dana jest wzorem:

du=dq+dw_obj.+dw_e

dq- ciepło dostarczone do układu [J]

dw_obj- praca zminy objętości wykonana na układ [J]

dw_e-dodatkowa praca wykonana przez układ np. elektryczna [J]

Gdy układ utrzymywany jest w stałej objętości i nie wykonuje innego rodz. pracy to:

du = dq_v

Objętość(v)- stosunek masy substancji do jej gęstości :

v = m/d [m³]

m- masa substancji [g]

d- gęstość substancji [g/m³]

Ciśnienie(p)- zdefiniowane jako normalna składowa siły do powierzchni na którą działa:

p = F/A [N/m²]

F- siła [N]

A- powierzchnia [m²]

[N]=[
]

---