Zadania z ekonomii matematycznej

V. MAKSYMALIZACJA UŻYTECZNOŚCI KONSUMPCJI. FUNKCJA POPYTU KONSUMENTA.

1. Jeżeli
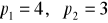
   , to jaki jest optymalny koszyk konsumenta o dochodzie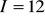
   i funkcji użyteczności f danej wzorem:

a)
;

b)
;

c)
;

d)
;

e)
.

2. Zakładamy, że konsument ma stałe dochody 24 złote. Dla każdego przypadku z zadania 1 znaleźć funkcję popytu na pierwszy towar dla funkcji użyteczności
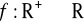
   , gdy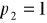
   .

3. Znaleźć funkcję popytu konsumenta na wermut, przy założeniu, że cena dżinu jest stała i wynosi 10 złotych za litr, a dochód konsumenta wynosi 1000 złotych. Doskonała mieszanka ma proporcje 10 części dżinu na 1 część wermutu.

4. Znaleźć funkcję popytu na drugi towar przy zmianie jego ceny mając dane:
   .

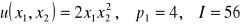
5. Konsument ma następującą funkcję użyteczności:

a)
,

b)
.

Wyznaczyć funkcję popytu konsumenta.

6. Obliczyć elastyczność funkcji
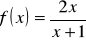
   dla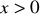
   , w punkcie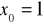
   .

7. Funkcja popytu na dobra podstawowe zależy od dochodu na osobę x i jest postaci
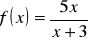
   , gdzie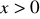
   . Obliczyć elastyczność dochodową funkcji f, gdy dochód na osobę wynosi 2 jednostki pieniężne. Wynik zinterpretować ekonomicznie.

8. Hortex wypuszcza na rynek dwa soki: pomarańczowy oraz jabłkowy po cenach odpowiednio
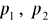
   . Funkcje popytu na soki są następujące: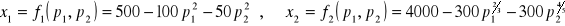
   Sprawdzić, czy te dwa towary są komplementarne, czy też konkurują ze sobą, badając wpływ zmiany ceny jednego towaru na popyt na drugi.

9. Jeśli krzywa popytu dana jest wzorem
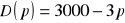
   , to jaka cena maksymalizuje przychody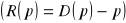
   ?

10. Krzywa popytu dana jest wzorem
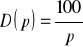
    . Przy jakiej cenie dochód będzie maksymalny?

11. Konsument może wydać 1280 zł. na dwa dobra X i Y, kosztujące odpowiednio 1 zł. i 16 zł. Jego funkcja użyteczności opisująca, jak ceni on sobie x jednostek dobra X i y jednostek dobra Y, dana jest wzorem
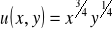
    . Użyć metody Lagrange'a do znalezienia wartości x i y maksymalizujących użyteczność.

12. Konsumenta charakteryzuje funkcja użyteczności Cobba-Douglasa postaci
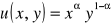
    . Parametr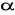
    nieznany, ale wiadomo, że natrafiając na problem maksymalizacji użyteczności przy warunku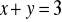
    konsument wybierze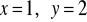
    .

10