ZAGADNIENIA TEORETYCZNE

Budowa wszystkich ciał makroskopowych jest cząsteczkowa, przy czym owe cząsteczki są w ciągłym ruchu i oddziaływają między sobą pewnymi siłami. Siły oddziaływania międzyatomowego są odpowiedzialne za powstawanie cząsteczek. Siły oddziaływania miedzy cząsteczkami prowadzą do tworzenia się struktur wielomolekularnych, w szczególności do powstania ciał stałych i cieczy. Zbliżanie do siebie atomów powoduje pojawienie się sił przyciągających, które najpierw wzrastają w miarę zmniejszania odległości miedzy jądrami atomów, a potem zmniejszają się aż w końcu przechodzą w siły odpychające. Gdy siła oddziaływania jest zerowa dla pewnej odległości r oraz energia potencjalna osiąga minimalną wartość cząstka jest w stanie równowagi trwałej. Ową odległość r nazywamy długością wiązania atomowego. Ze względu na strukturę wiązań możemy wyróżnić wiązania jonowe (powstają w wyniku przyciągania się elektrostatycznego) oraz kowalencyjne (powstaje dzięki 2 elektronom - po jednym z każdego atomu - ale jako para należą jednocześnie do jednego jak i drugiego atomu).

W przypadku cząsteczki wody atomy wodoru połączone są z atomem tlenu wiązaniem kowalencyjnym. W cząsteczce wody ładunek ujemny jest przesunięty w kierunku atomu tlenu (większa zdolność przyciągania elektronów przez atomy tlenu), a co za tym idzie - ładunek dodatni jest przesunięty w kierunku atomów wodoru. W rezultacie cząsteczka wody ma charakter dipolowy (o określonym momencie dipolowym).

W cieczach odległości między cząsteczkami są porównywalne z ich wymiarami, dlatego ważne są też oddziaływania między cząsteczkowe. W wodzie występują tzw. siły van der Wallsa. Są to siły międzycząsteczkowe w krysztale, mające tę samą naturę co siły przyciągania się cząsteczek w gazach.

W przypadku wody, elektrycznie spolaryzowane cząsteczki łączą się z sąsiednimi cząsteczkami wiązaniami wodorowymi (słabe wiązanie tworzące mostek wodorowy). Przyjmuje się, że struktura wody ma charakter kwazikrystaliczny (zmienny w czasie), o uporządkowaniu bliskim względem najbliższych sąsiadów. Woda zawiera cząsteczki swobodne, ale również grupy cząsteczek powiązanych ze sobą wiązaniami wodorowymi. Te właśnie wiązania wodorowe są odpowiedzialne za oddziaływania cząsteczek i za szczególne właściwości wody i lodu. Większość cieczy zwiększa swoją objętość wraz ze wzrostem temperatury. Woda jest jednak wyjątkiem. Powyżej 4
zachowuje się „normalnie” jednak w zakresie temperatur od 0
do 4
kurczy się aby w temperaturze 4
mieć najmniejszą objętość (największą gęstość). Wynika z tego, że obniżając temperaturę woda rozszerza się. Jest to skutkiem asocjacji (łączenia się) cząsteczek wody, w wyniku czego w temperaturze 0
tworzy się heksagonalna struktura lodu z dużymi otwartymi przestrzeniami między ściankami kryształu. Konsekwencją takich procesów jest zwiększenie objętości wody o około 10%. W czasie topnienia wiązania wodorowe pękają a kryształki przechodzą w stan ciekłej wody.

OPIS DOŚWIADCZENIA

Aby zaobserwować rozszerzalność wody w zależności od temperatury posłużyliśmy się specjalnym naczyńkiem z kapilarą. Dzięki mieszaninie chłodzącej (lód i sól) mogliśmy obniżyć temperaturę wody do 0
. Do ogrzania posłużyło nam otaczające powietrze.

Jak można było się spodziewać i jak wynika z wykresu woda w czasie ochładzania zmniejszała swoją objętość, tak długo, aż osiągnęła temperaturę 4
. W czasie dalszego ochładzania poziom wody w kapilarze zaczął się podnosić. Warto przy tej okazji zauważyć, iż wykres ma charakter paraboliczny. Oznacza to, iż w miarę jak temperatura spadała ku 4
objętość wody malała coraz wolniej natomiast po przekroczeniu tej temperatury i zbliżaniu się ku 0
poziom wody rósł szybciej.

Odwrotna sytuacja miała miejsce, gdy naczyńko wyjęliśmy z mieszaniny chłodzącej (ogrzewanie). Wraz ze wzrostem temperatury woda „kurczyła” się do temperatury 4
, w której ponownie osiągnęła minimum swojej objętości. W trakcie dalszego podnoszenia temperatury poziom wody również zaczął wzrastać. Podobnie jak w przypadku ochładzania wykres także przypomina parabolę.

Maksymalny przyrost wysokości słupa wody w doświadczeniu wniósł 30 milimetrów dla temperatury 11
- przy czym 0 milimetrów przyjmujemy dla 4
. Wysokość słupa wody dla 0
wyniosła 12 milimetrów.

Wiemy, że gęstość jest to ilość masy przypadającej na daną objętość. Biorąc pod uwagę, że masa wody w doświadczeniu nie zmieniała się, łatwo wywnioskować, iż największa gęstość była w momencie najmniejszej osiągniętej objętości - czyli w temperaturze 4
.

Aby obliczyć maksymalną gęstość skorzystamy z danych tablicowych. Otóż gęstość wody dla temperatury 10°C wynosi δ=0,9997*10³ [kg*m^-3]. Masa wody jest stała.

Czyli:

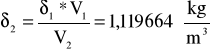
Przyjąłem, że wysokość kapilarki w temperaturze 10°C jest równa 0,25m+0,03m, natomiast w temperaturze 4°C (największa gęstość była w momencie najmniejszej osiągniętej objętości - czyli w temperaturze 4
). jest równa 0,25m

WNIOSKI

Doświadczenie to pokazało, iż woda zachowuje się inaczej niż inne ciecze. Dodatkowo można zauważyć, że objętość wody nie zależy od temperatury w sposób liniowy. Można się domyślać, iż przy dalszym podnoszeniu temperatury powyżej 11
(ochładzaniu poniżej 0
- przejście wody w stan stały skupienia) woda rozszerza się bardzo szybko. Ciekawe jest też to, że wykres nie jest symetryczny względem prostej przechodzącej przez punkt 4
. Ćwiczenie tłumaczy też zjawisko unoszenia się lodu na powierzchni wody. Lód ma o wiele mniejszą gęstość niż woda i właśnie dlatego może w niej pływać.

Dokładność pomiaru temperatury wynosi 0,1°C. Odczyt temperatury wydaje mi się, iż był prawidłowy, ponieważ temperatura wody w całym naczyńku była równomierna (dzięki mieszadełku).

Natomiast dokładność pomiaru wysokości słupa w kapilarze wynosi 1mm.

---