Całki

F.pierwotna - Jeśli dana jest ciągła f. f, to f.ą pierw.ą nazyw. taką f.ę F, że F'(x)=f(x)

Także każda suma [F(x)+C]'=f(x)

Całka nieoznaczona

C.nieoz. z f.i f nazyw. Rodzinę f.i pierwotnych i oznaczamy symbolem

Własności:

Wzory:

Metody całkowania

-przez części

-podstawienie

Całka oznaczona

Suma całkowa-suma pól elementarnych prostokątów

W sensie Riemana:

"Jeśli f. f jest dodatnia w<a;b>,to całka oz.=polu obszaru ogr.od góry wykresem f.i, pr. x=a i x=b oraz osią OX"

Układy równań liniowych

Ukł.lin.- wyraż. Postaci ax_i1x₁+ax_i2x₂+...+ax_inx_n=b_i

_{i=1,...,m. m.-il.równań}

post.macierzowa A_x=b; A=(a_ij); x=[ ]; b=[ ]

Układ Cramera, gdy:

A∈ Rⁿⁿ (kwadratowa)

detA≠0

Tw. Sylwestra

War. koniecz. dodatniej (ujemnej) określon. Formy kwadr. F(x)=x^TAx jest by wszystkie minory główne mac. A były dodatnie (nieparzyste ujemne).

Δ_n >0 ((-1)ⁿΔ_n >0)

Tw. Croneckera-Capelli'ego

War.konieczny rozwiązalności ukł. równań:

rA=rA|U (≠to u. sprzeczny)

-jeśli rA=rA|U=n to 1 rozw

Ukł. zreduk. - ukł. powst. ze skreślenia m-r równań i wprow. n-r parametrów.

Baza przest. Liniowej

Jeśli dana jest p. lin. V nad ciałem liczb R, to bazą tej p. nazyw. układ wekt. a₁,...,a_kV taki że:

-Liniowo niezależny

-Którego liczebność z/wzgl na lin. niezal.

Przekszt. Liniowe

Dla danej f. f:V₁→V₂ (V-prz.liniowe nad ciałem R) nazyw. ją przeksz. lin., jeśli

f(a+b)=f(a)+f(b)

f(αa)= αf(a)

Podprz. lin. p. lin.

Podzbiór L p.lin. V (L⊂V) jest podprz. prz. V, jeśli sam z/wzgl na działania określone w V jest p .lin.

War.Kon i Wyst. :

Dla każ. α,β∈R i a,bL

Forma liniowa

Przeksz.liniowe F:RⁿR

F(x)=a₁x₁+...+a_nx_n

Forma dwulinowa

Przeksz.:RⁿxR^m→

zapis w post. z=Φ(x,y),

z∈R^p, x∈Rⁿ, y∈R^m

war: jest ono liniowe z/wzgl na x (przy ustal. y) i lin. z/wzgl na y (ust. x)

Forma kwadratowa

Prz. dwuliniowe, gdzie:

P=1, n=m., y=x

Funkcja typu F:Rⁿ→R

Określoność :

Dla x≠0 F(x)>(<)0

Dodatnio(ujemnie)

Półokr. Dod (uj) ≥ (≤)0

Ciało liczbowe

Struktura alg.,złoż. Ze zbioru: dwóch działań + i *, określonych na el.ach tego zb., mająca własn. Działań zbioru R (el. eutr. z/wzgl + i *, el. odwr. do dan. z/w *, el. przec. z/w +, rozdz.* wzgl. +)

Liczby zespolone

z=a+bi, i²=-1

postać Trygon.:

z=|z|*(cosf+isinf)

tw. Moivre'a-Laplace'a

(cosf+isinf)ⁿ=cosnf+isinnf

Przestrzeń liniowa

P.lin. nad ciałem R(ogólnie K) naz. Zbiór V z dwoma dział. + i * (<V;⊕;⊗>) gdzie ⊕: RxV→V i ⊗:RxV→V i dział te spełniają własności:

a+b=b+a

a+(b+c)=(a+b)+c

a+0=a el. neutr.dod.

a+(-a)=0 el. przec.

1*a=a el. neu. mnoż.

c(a+b)=ca+cb (rozdz. * wzgl +)

(ab)c=a(bc) (łączność mnożenia)

(nie)zależność liniowa wektorów

Dla ukł. wektorów a₁,...,a_k∈V/R (nad ciałem R): wektory są linowo niezal., jeśli dla liczb α₁,...,α_k∈R, czyli dla α₁a₁,...,α_ka_k=0^ (*)∈V, α₁=...=α_k=0

Ukł jest zal. gdy nie jest niezal.

W niezal gdy jednocześnie wszystkie α nie są =0, to spełn. jest równ (*).

W zal. co najmn. 1 wektor zależy od pozost. wektorów

Praca pochodzi z serwisu www.e-sciagi.pl

---
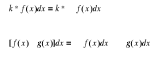
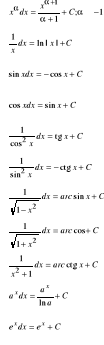