ANOVA - AB - sumy kwadratów

Wynik k-tej osoby przypisanej (losowo!) do ij-tej

(i = 1, ..., p; j = 1, ..., q) grupy tworzy liniową kombinację elementów:

• średniej ogólnej (ၠY_...), która jest średnią z próby losowo pobranej z populacji o średniej ၭ

• odchylenia średniej z i-tej grupy (ၠY_i..) od średniej ogólnej (ၠY_...), czyli:
  ၠY_i.. - ၠY_...

• odchylenia średniej z j-tej grupy (ၠY_.j.) od średniej ogólnej (ၠY_...), czyli:
  ၠY_.j. - ၠY_...

• odchylenia średniej ij-tej grupy (ၠY_ij.) od średnich brzegowych: ၠY_i.. , ၠY_.j. oraz średniej ogólnej ၠY_..., czyli: ၠY_ij. - ၠY_i.. - ၠY_.j. + ၠY_...

• odchylenia k-tej osoby z ij-tej grupy (Y_ijk) od średniej ij-tej grupy, czyli:
  Y_ijk - ၠY_ij.

Oszacowaniami:

1. 
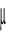
   jest ၠY_...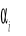

2. 
   = ၭ_i.. - ၭ_... czyli efektu i-tego poziomu czynnika A jest różnica: ၠY_i.. - ၠY_...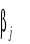

3. 
   = ၭ_.j. - ၭ_... czyli efektu j-tego poziomu czynnika B jest różnica: ၠY_.j. - ၠY_...

(4)
= ၭ_ij. - ၭ_... - ၡ_i - ၢ_j =
ၭ_ij. - ၭ_... - (ၭ_i.. - ၭ_... ) - (ၭ_.j. - ၭ_...) =
ၭ_ij. - ၭ_i.. - ၭ_.j. + ၭ_...
czyli efektu interakcyjnego i-tego poziomu czynnika A z j-tym poziomem czynnika B jest wyrażenie: ၠ
Y_ij. - ၠY_i.. - ၠY_.j. + ၠY_...

(5) ၥ_ijk czyli błędu eksperymentalnego jest różnica: Y_ijk - ၠY_ij.

Model ijk-tego wyniku - na poziomie populacji :

Y_ijk = ၭ + ၡ_i + ၢ_j + ၡ_iၢ_j + ၥ_ijk

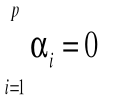
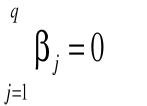
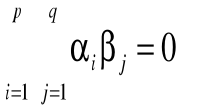
Wynik ijk-tej osoby, na poziomie próby:

Y_ijk = ၠY_... + [(ၠY_i.. - ၠY_...) + (ၠY_.j. - ၠY_...) +
(ၠY_ij. - ၠY_i.. - ၠY_.j. + ၠY_...) + (Y_ijk - ၠY_ij.)]

Odchylenie pojedynczego wyniku od średniej ogólnej:

Y_ijk - ၠY_... = [(ၠY_i.. - ၠY_...) + (ၠY_.j. - ၠY_...) +
(ၠY_ij. - ၠY_i.. - ၠY_.j. + ၠY_...) + (Y_ijk - ၠY_ij.)]

Podnosząc obie strony równania do kwadratu:

SS_cała = SS_A + SS_B + SS_AB + SS_błąd

SS_cała =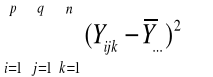

SS_A =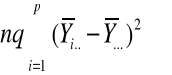

SS_B =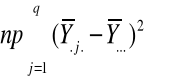

SS_AB =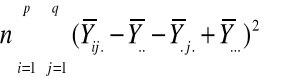

SS_błąd =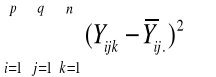

1