Analiza danych statystycznych

Przez 10 kolejnych miesięcy prowadzono badania skłonności potencjalnych klientów do korzystania z nowej usługi. Odsetek (w procentach) osób wyrażających zainteresowanie nową usługą wynosił w kolejnych miesiącach:

51,9 64,1 57,3 58,1 55,7 62,2 67,8 64,1 54,8 60,9

Wyznacz miary wartości średniej i oceń zmienność danych.

s =

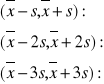
Zadanie 1: Obliczyć prawdopodobieństwo wyrzucenia kostką do gry liczby mniejszej od 3.

Zadanie 2: Badaniu poddano dochody 100 rodzin. Przeciętne miesięczne dochody na członka rodziny zostały pogrupowane i przedstawione w tabeli

Dochód	Liczba rodzin
poniżej 200 zł	18
200 zł - 300 zł	24
300 zł - 400 zł	30
powyżej 400 zł	28

Jakie jest prawdopodobieństwo, że losowo wybrana rodzina ma przeciętny dochód na jej członka większy od 300 zł.

Zadanie 3. Badano wyposażenie 100 małych firm w sprzęt telekomunikacyjny. Rezultaty badania są następujące:

Wyłącznie telefon	42 firmy
Telefon + fax	36 firm
Telefon i osobny fax	22 firmy

Jakie jest prawdopodobieństwo, że wybrana losowo firma ma dostęp do faxu.

Zadanie 4. Jakie jest prawdopodobieństwo wyrzucenia kostką do gry dwu kolejnych liczb większych od 4.

Zadanie 5. W badaniach rynku ustalono, że ocena funkcjonalna pewnego urządzenia oraz ocena estetyczna (wyglądu) są wzajemnie niezależne. W rezultacie analizy wyników badań ustalono, że prawdopodobieństwo pozytywnej oceny funkcjonalnej wynosi 0,9, zaś prawdopodobieństwo pozytywnej oceny estetycznej wynosi 0,8. Ustalono ponadto, że potencjalnymi klientami są przede wszystkim te osoby, które dane urządzenie oceniają pozytywnie zarówno od strony funkcjonalnej jak i estetycznej. Producent zamierza zaoferować 10 000 urządzeń. Na sprzedaż jakiej liczby (średnio) urządzeń można liczyć, jeżeli nie zostanie przeprowadzona dodatkowa akcja promocyjna.

Zadanie 6. Obliczyć prawdopodobieństwo wyrzucenia w dwu rzutach kostką do gry przynajmniej jednej szóstki.

Zadanie 7. Przyjmując warunki zadania 5 ocenić, ilu byłoby potencjalnych klientów, gdyby do zakupu wystarczała przynajmniej jedna ocena pozytywna.

Obliczanie prawdopodobieństw w przypadku

rozkładu normalnego

X - zmienna losowa o rozkładzie normalnym N(,s)

 - wartość oczekiwana

σ - odchylenie standardowe

Standaryzacja zmiennej losowej o rozkładzie normalnym

Dystrybuanta: F(y) = P(Y<y) = (y) (Tablice !!!!)

(-y) = 1 - (y)

Zadanie 8. Wzrost grupy osób opisany jest rozkładem normalnym o wartości oczekiwanej 173 cm oraz odchyleniu standardowym σ=6 cm.

a) Oblicz prawdopodobieństwo, że losowo wybrana osoba ma nie więcej niż

a1) 179 cm, a2) 181 cm, a3) 165 cm

b) Jaka frakcja tych osób ma wzrost pomiędzy 167 cm a 179 cm?

Kwantyl standaryzowanego rozkładu normalnego N(0,1)

X ~ N(,s)

Zadanie 9. Dla danych z zadania 8 wyznaczyć wartość wzrostu, którego nie przekracza 60% badanej populacji osób.

	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
0.90	1.282	1.287	1.293	1.299	1.305	1.311	1.317	1.323	1.329	1.335
0.91	1.341	1.347	1.353	1.359	1.366	1.372	1.379	1.385	1.392	1.398
0.92	1.405	1.412	1.419	1.426	1.433	1.440	1.447	1.454	1.461	1.468
0.93	1.476	1.483	1.491	1.499	1.506	1.514	1.522	1.530	1.538	1.546
0.94	1.555	1.563	1.572	1.580	1.589	1.598	1.607	1.616	1.626	1.635
0.95	1.645	1.655	1.665	1.675	1.685	1.695	1.706	1.717	1.728	1.739
0.96	1.751	1.762	1.774	1.787	1.799	1.812	1.825	1.838	1.852	1.866
0.97	1.881	1.896	1.911	1.927	1.943	1.960	1.977	1.995	2.014	2.034
0.98	2.054	2.075	2.097	2.120	2.144	2.170	2.197	2.226	2.257	2.290
0.99	2.326	2.366	2.409	2.457	2.512	2.576	2.652	2.748	2.878	3.090

Tabela D.1 Kwantyle y_ standaryzowanego rozkładu normalnego (y_1-= -y­_).

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

---