Postać bazowa macierzy.

Operacją elementarną na macierzy nazywamy każde z następujących przekształceń

1. przestawienie dwóch wierszy (kolumn),

2. pomnożenie wiersza (kolumny) przez liczbę różną od zera,

3. dodanie do danego wiersza (kolumny) innego wiersza (innej kolumny) pomnożonego przez dowolną liczbę.

Mówimy, że macierze A i B są równoważne (zapisujemy A~B) jeśli macierz B powstaje z macierzy A przez wykonanie skończonej liczby operacji elementarnych.

postać bazowa macierzy

Dowolną niezerową macierz A o wymiarach m na n za pomocą ciągu przekształceń elementarnych można sprowadzić do postaci

zwanej bazową (kanoniczną).

Szczególne przypadki macierzy bazowej:

dla

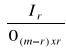
dla

dla

Rząd macierzy

Def:

Rzędem niezerowej macierzy A_mxn nazywamy liczbę równą stopniowi macierzy jednostkowej występującej w jej postaci bazowej.

oznaczenie: rzA.

Dodatkowo przyjmujemy, że rząd macierzy zerowej jest równy zeru.

Rząd macierzy jest równy maksymalnej liczbie różnych kolumn jednostkowych w postaci bazowej.

Własność

Rząd macierzy A o wymiarach m na n jest nie większy od mniejszej z liczb m i n.

.

Tw: Macierze równoważne mają równe rzędy.

Jeżeli A~B, to rzA=rzB.

UKŁADY RÓWNAŃ LINIOWYCH

Układ m równań liniowych o n niewiadomych x₁, x₂, ... , x_n

ma następującą postać

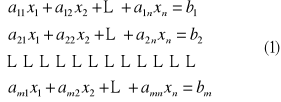
gdzie współczynniki układu a_ij i wyrazy wolne b_i (i=1, 2,..., m, j=1, 2,..., n ) są danymi liczbami rzeczywistymi.

Z układem równań liniowych (1) związane są macierze:

A_mxn macierz współczynników,

b_mx1 macierz (kolumna, wektor) wyrazów wolnych,

x_nx1 macierz (kolumna, wektor) niewiadomych,

macierz rozszerzona (uzupełniona).

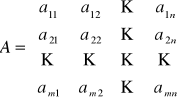
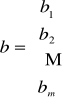
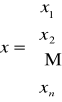
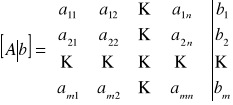
Rozwiązaniem układu nazywamy każdy ciąg n liczb (c₁, c₂, ... , c_n) spełniający wszystkie równania układu tzn.

Układ równań liniowych nazywamy

• jednorodnym, jeżeli wektor b wyrazów wolnych jest zerowy.

• niejednorodnym, jeżeli wektor bႹ0.

Układ równań liniowych nazywamy

• sprzecznym, gdy nie posiada żadnego rozwiązania,

• oznaczonym, gdy ma dokładnie jedno rozwiązanie,

• nieoznaczonym, gdy ma nieskończenie wiele rozwiązań.

Innych możliwości nie ma.

Metoda eliminacji Gaussa.

Rozwiązywanie układów równań liniowych metodą operacji elementarnych

Przekształceniami (operacjami) elementarnymi układu równań liniowych nazywamy:

1. przestawienie dwóch równań układu,

2. pomnożenie równania układu przez liczbę różną od zera,

3. pomnożenie równania układu przez dowolną liczbę i dodanie do innego równania układu.

Równanie postaci

nazywamy równaniem tożsamościowym.

Każdy ciąg n liczb spełnia to równanie.

Jeśli dany układ równań przekształcimy za pomocą skończonej liczby operacji elementarnych oraz pominiemy równania tożsamościowe, to otrzymamy układ równoważny danemu, to znaczy o takim samym zbiorze rozwiązań.

Przekształceniom elementarnym układu równań odpowiadają przekształcenia elementarne na wierszach macierzy rozszerzonej tego układu

1. przestawienie dwóch wierszy,

2. pomnożenie wiersza przez liczbę różną od zera,

3. pomnożenie pewnego wiersza przez dowolną liczbę i dodanie do innego wiersza.

Metoda eliminacji Gaussa

Macierz rozszerzoną dowolnego układ m równań liniowych z n niewiadomymi za pomocą przekształceń elementarnych na wierszach macierzy rozszerzonej i przestawiania kolumn w macierzy współczynników można sprowadzić do postaci

~

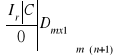
Taką postać układu równań nazywamy postacią bazową.

Uwaga!

Przestawianie kolumn w macierzy współczynników oznacza zmianę kolejności niewiadomych.

3

---