Test dla wartości średniej

Przykład 1- duża próba

W 81 wylosowanych zakładach zbadano koszty materiałowe pewnego wyrobu i otrzymano średnią
. Na poziomie istotności α = 0,05 zweryfikować hipotezę, że średnie koszty materiałowe przy produkcji tego wyrobu wynoszą 600 zł.

Stawiamy hipotezy:

H₀: E(X) = 600 H₁: E(X) ≠ 600

Statystyka testowa

Test jest dwustronny zatem ‌׀‌t‌‌׀ = 3,6

n =81 > 30 duża próba zatem t_α odczytujemy z rozkładu normalnego N(0, 1), korzystając z zależności

Czyli ‌׀‌t‌‌׀ = 3,6 > t_α = 1,95 co oznacza, że H₀ należy odrzucić i przyjąć H₁, oznaczającą, że średnie koszty materiałowe przy produkcji tego wyrobu nie wynoszą 600 zł.

Przykład 2- duża próba

Firma rozwożąca paczki na terenie Wrocławia zapewnia, że średni czas dostarczenia paczki do klienta = 28 minut.

Należy to sprawdzić, czyli

H₀: E(X) = 28 H₁: E(X) ≠ 28

Na podstawie próby losowej liczącej n =100 paczek policzono

Oraz wyznaczono statystykę testową

Dla poziomu istotności α = 0,05

Zatem ‌׀‌t‌‌׀ = 7 > t_α = 1,95 co oznacza, że H₀ należy odrzucić i przyjąć H₁, oznaczającą, że średni czas dostarczenia paczki nie wynosi 28 minut.

Przykład 3 - mała próba

Firma Canon wprowadziła na rynek nową kopiarkę, z nowymi możliwościami. Przeciętna prędkość działania kopiarek tego typu wynosi 27 kopii na minutę. Firma chce sprawdzić, czy nowa kopiarka ma tę samą prędkość działania.

Przeprowadzono 24 próby i otrzymano
.

Czy na poziomie α = 0,05 można sądzić, że przeciętna prędkość kopiowania nowej kopiarki istotnie różni się od prędkości kopiowania standardowych kopiarek?

H₀: E(X) = 27 H₁: E(X) ≠ 27

n = 24 (mala próba) to dla α = 0,05 oraz dla n-1 = 23 stopni swobody z tablic rozkładu Studenta odczytujemy t_α = 2,069

Zatem ‌׀‌t‌‌׀ = 1,555 < t_α = 2,069 co oznacza, że brak podstaw do odrzucenia H₀ , że przeciętna prędkość kopiowania nowej kopiarki nieistotnie różni się od prędkości kopiowania standardowych kopiarek

Przykład 4 - mała próba

Producent czekolady zapewnia, że jej trwałość wynosi przeciętnie 65 tygodni. Konkurent podejrzewa, że przeciętna trwałość jest mniejsza. W próbie 21 czekolad okazało się, że średnia trwałość wynosi 62,5 tygodni z s= 3 tygodnie.

Na poziomie istotności 0,01 sprawdzić czy jest podstawa do uznania zapewnień producenta za fałszywe.

H₀: E(X) = 65 H₁: E(X) < 65 (test lewostronny) n = 21 (mała próba - korzystamy z rozkładu Studenta)

α = 0,01 to 2* α = 0,02 oraz dla n-1 = 20 stopni swobody z tablic rozkładu Studenta odczytujemy

t_α = 2,528 a symetrycznie - t_α = - 2,528

Zatem t = - 3,727 < - 2,528=- t_α czyli H₀ należy odrzucić i przyjąć H₁, oznaczającą, że zapewnienia producenta były fałszywe.

Przykład 5 - test dla dwóch średnich (wartości oczekiwanych)

Należy zbadać, czy słuszne jest stwierdzenie, że zatrudnione kobiety na tych samych stanowiskach co mężczyźni (w przemyśle) otrzymują przeciętnie niższą płacę. W tym celu:

Wylosowano n₁ - 100 kobiet i otrzymano
, s₁=80 zł

Oraz n₂=80 mężczyzn;

; s₂=100 zł.

Na poziomie α=0,01 sprawdzić hipotezę, że płace kobiet są niższe niż płace mężczyzn.

H₀: E(X₁) = E(X₂) H₁: E(X₁) < E(X₂) n₁, n₂ > 30 to duża próba

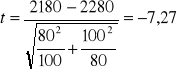
Z tablic N(0, 1) odczytujemy dla
t_α= - 2,33 (bierzemy wartość ujemną bo test jest lewostronny)

t = - 7,27 < t_α = - 2,33 to H₀ odrzucamy i przyjmujemy H₁ kobiety zarabiają mniej.

Przykład 6 - test dla dwóch wskaźników struktury (frakcji, procentów)

W celu sprawdzenia czy zachorowalność na gruźlicę w mieście i na wsi jest taka sama wylosowano:

n₁ = 1200 osób z miasta i otrzymano X = 40 chorych na gruźlicę oraz

n₂ = 1500 osób ze wsi i otrzymano Y = 100 chorych na gruźlicę.

Na poziomie α = 0,05 zweryfikować hipotezę o jednakowym procencie chorych w mieście i na wsi.

H₀: p₁ = p₂ H₁: p₁ ≠ p₂

Z próby obliczamy
oraz

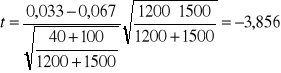
ǀtǀ = 3,856 > t_α= 1,95 czyli odrzucamy H₀

Przykład 7 - test dla współczynnika korelacji

Na podstawie 10 elementowej próby studentów policzono korelację między średnimi ich ocen a liczbą godzin poświęconych nauce i otrzymano r = 0,83.

Na poziomie α = 0,05 sprawdzić, że istnieje korelacja między wynikami studentów a czasem ich nauki

H₀: r = 0 H₁: r ≠ 0

n =10 (mała próba) to t_α= 2,306, odczytujemy z tablic Studenta dla α = 0,05 i n - 2 = 8 stopni swobody

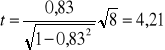
ǀtǀ = 421 > t_α = 2,306 czyli odrzucamy H₀

Na podstawie A.D Aczel, Statystyka w zarządzaniu, Wydawnictwo Naukowe PWN, Warszawa

---