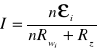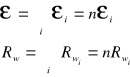18.Model przewodnictwa elektrycznego Ruch ładunków może mieć miejsce w ciałach zwanych przewodnikami, a w pewnych warunkach również w półprzewodnikach; dielektryki natomiast nie przewodzą prądu. Nośnikami ładunków w przewodnikach mogą być zarówno ładunki dodatnie jak i ujemne, zależnie od rodzaju przewodnika. W metalach swobodnie przemieszczają się tylko elektrony-są to przy tym nie wszystkie elektrony danego metalu, lecz tylko elektrony najsłabiej związane z jądrem, a więc pochodzące powłoki zewnętrznej-elektrony przewodnictwa. W cieczach nośnikami prądu elektrycznego są jony dodatnie-kationy i jony ujemne-aniony. W rozrzedzonych gazach nośnikami prądu są elektrony i jony. Za umowny kierunek prądu przyjmuje się kierunek ruchu nośników dodatnich. Natężenie prądu jest wielkością makroskopową charakteryzującą przepływ prądu w całości. Aby ilościowo scharakteryzować rozkład prądu na przekroju poprzecznym, wprowadzono wielkość mikroskopową zwaną gęstością prądu. Definiuje się ją w przypadku równomiernego rozkładu prądu w przekroju poprzecznym jako iloraz j=dI/dA_n przy czym przez A rozumie się powierzchnie prostopadłą do kierunku uporządkowanego ruchu ładunków. Gęstość mierzy się w amperach na metr kwadratowy. Warunki przepływu prądu elektrycznego 1.istnienie w danym ośrodku nośników prądu, które mogą się przemieszczać 2. istnienie w danym ośrodku pola elektrycznego, którego energia może być wydatkowana na przemieszczenie nośników prądu. Do podtrzymania przepływ prądu elektrycznego przez czas dłuższy(prąd stacjonarny), niezbędne jest kompensowanie strat energii pola elektrycznego związanych z praca przemieszczenia nośników prądu(źródło siły elektromotorycznej).

19.Prawo Ohma Stosunek napięcia między dwoma punktami przewodnika do natężenia przepływającego przezeń prądu jest wielkością stałą i nie zależy ani od napięcia ani od natężenia prądu. I=U/R gdzie R-oporność danego przewodnika, mierzona w omach. Lokalna postać prawa Ohma: Jeżeli w dowolnym obszarze przewodnika, o elektrycznej przewodności γ wytworzymy pole elektryczne o natężeniu Ē to w obszarze tym popłynie prąd przewodnictwa o gęstości: ĵ= γĒ [j=A/m²]. Kierunek i zwrot wektora gęstości prądu j określa wektor natężenia pola elektrycznego Ē. Przyłożenie napięcia do końców przewodnika powoduje, iż zaczyna przepływać prąd. Doświadczenie pokazuje, że w przewodnikach metalicznych natężenie prądu jest dla danego przewodnika wprost proporcjonalne do przyłożonego napięcia I=GU Współczynnik proporcjonalności G nazywa się przewodnością. Prawo Ohma dla obwodu zamkniętego-Każde rzeczywiste źródło siły elektromotorycznej posiada pewien opór wewnętrzny r. Po dołączeniu do źródła oporu zewnętrznego R, w obwodzie popłynie prąd elektryczny zarówno przez opór zewnętrzny R jak i przez opór wewnętrzny r. Natężenie płynącego w obwodzie prądu opisane jest prawem Ohma dla obwodu zamkniętego. I=ε/(R+r)

20.Prawa Kirchoffa W praktycznym zagadnieniach spotyka się obwody elektryczne rozgałęzione zawierające pewna liczbę źródeł SEM. Przy znajdowaniu napięć i natężeń prądów korzystamy z praw Kirchoffa. Pierwsze prawo: W dowolnym węźle obwodu suma algebraiczna natężeń prądów wpływających i wypływających do węzła równa się zeru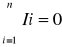

Węzłem obwodu(punktem rozgałęzienia) nazywa się punkt, który łączy się pewna liczba gałęzi obwodu. Drugie prawo: W dowolnym oczku sieci elektrycznej, algebraiczna suma działających w nim sił elektromotorycznych równa jest algebraicznej sumie spadków potencjału na poszczególnych oporach.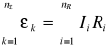
Przyjmujemy określony kierunek obiegu oczka. Siły elektromotoryczne uważamy za dodatnie, gdy wytwarzany przez nie prąd ma kierunek zgodny z przyjętym kierunkiem obiegu oczka. Natężenie prądów o kierunku zgodnym z przyjętym kierunkiem obiegu oczka uważamy za dodatni.

21.Zależność oporu od temperatury Opór elektryczny przewodnika R zależy od temperatury T. Dla czystych metali, w określonym zakresie temperatury R=R₀[1+α(T-T₀)] R₀-opór przewodnika metalicznego w temperaturze odniesienia(zwykle T₀=273,14K) temperaturowy współczynnik oporu α=1/R₀*dR/dT Zależność oporu od temperatury jest konsekwencją analogicznej zależności oporu właściwego ρ tych przewodników od temperatury ρ= ρ₀[1+ α(T-T₀)]

22.Prawo Wiedemana Franza Omawiając zależność oporu, czy też przewodnictwa właściwego od temperatury, należy wspomnieć o związku pomiędzy przewodnictwem cieplnym a przewodnictwem elektrycznym. Nazywa się to prawem Wiedemana Franza: Jeżeli przez * oznaczymy współczynnik przewodnictwa cieplnego, a przez * współczynnik przewodnictwa elektrycznego, to dla stałej temperatury T. Oznacza to, że dobre przewodniki ciepła są też dobrymi przewodnikami elektryczności

23.Prawo Joule'a Lenza Prąd płynący przez opornik wykonuje pracę. Można ją łatwo wyznaczyć, jeśli wziąć pod uwagę dodatni ładunek q, jaki przenosi prąd o natężeniu I w czasie t. Ładunek porusza się od potencjału wyższego do niższego. Zatem pole istniejące w przewodniku wykonuje pracę W=qU, gdzie U oznacza napięcie między końcami opornika. Ponieważ q=It, więc praca ta ostatecznie wynosi W=Uit. Korzystając ze związku między napięciem na oporniku a prądem płynącym przez niego, pracę prądu można tez wyrazić za pomocą wzorów W=U²t/R=I²Rt. Praca ta zamienia się na ciepło i powyższe wzory określają jednocześnie ilość ciepła wydzielającego się w oporniku: Q=Uit=U²t/R=I²Rt.Ciepło mierzy się w dżulach. Podane zależności stanowią treść prawa Jouel'a-Lenza: prąd płynący przez opornik powoduje wydzielenie się w nim ciepła w ilości określonej wzorem Q=Uit=U²t/R=I²Rt. Korzystając z definicji mocy P=dW/dt otrzymamy P=UI=U²/R=I²R Różniczkowa postać prawa opisuje warunki wydzielania się energii cieplnej w określonym obszarze przewodnika. Jeżeli w dowolnym obszarze przewodnika o elektrycznej przewodności właściwej γ wytworzymy pole elektryczne o natężeniu Ē to w obszarze tym popłynie prąd przewodzony o gęstości ĵ powodując wydzielenie mocy cieplnej o gęstości objętościowej w równej iloczynowi skalarnemu wektorów ĵ i Ē. w= ĵĒ= γE² w=P/V-gęstość objętościowa mocy cieplnej

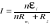
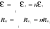
24.Łączenie ogniw Łączenie szeregowe

gdy R_z>>nR_w dostajemy większą siłę elektromotoryczną oraz większe natężenie. Łączenie równoległe ε= ε_i R_w=R_wi/n natężenie prądu będzie równe ε_i/R_z+R_wi/n Gdy Rz >> nRw prąd jest taki sam jak dla jednego ogniwa. Gdy Rz << Rw, prąd jest n razy większy. Łączenie mieszane W każdym szeregu mamy n baterii, i połączonych równolegle m szeregów. Każda bateria ma opór wewnętrzny Rwi. Siła elektromotoryczne wynosi: ε= nε_i Całkowity opór takiego połączenia wynosi; R=n(R_wi/m). Natężenie prądu, które popłynie w obwodzie, gdy włączymy baterię w obwód o oporze Rz, będzie równe: I=nε_i/(nR_wi/m +R_z) Gdy mamy łącznie (m · n) ogniw, uzyskamy maksymalny prąd , gdy; m/n=R_w/R_z

25.Dzielnik napięcia I=U/R U_x=IR_x U_x=UR_x/R .W przypadku gdy obciążymy dzielnik oporem RA napięcie Ua ulegnie zmianie na UA' , przy czym U_A'=I'R'₁ U_A'=U/(1+ R₂(R₁+R_A)/R₁R_A

26.Mostek Wheatstonne'a Wartość R_s jest dobierana tak długo, dopóki punkty a i b nie osiągną jednakowego potencjału(warunek ten można sprawdzić włączając na chwilę miedzy punktami a i b czuły przyrząd pomiarowy, jeżeli punkty te mają jednakowy potencjał, wskazówka przyrządu nie wychyli się)Pokazać, że gdy to nie jest spełnione, zachodzi następujący związek: R_x=R_sR₂/R₁ Przy pomocy tego urządzenia możemy mierzyć nieznane opory(R_x) w jednostkach oporu wzorcowego.

27.Metoda kompensacyjna pomiaru napięcia Metoda ta jest podobna do wyznaczania oporów w oparciu o mostek Wheatstone'a. Zmieniamy ustawienie suwaka na oporze AB tak długo, aż w galwanometrze przestanie płynąć prąd. Wtedy wiemy, że; I_x=I₀₂ Prąd w każdej gałęzi jest algebraiczną sumą prądów pochodzących od każdej siły elektromotorycznej oddzielnie, przy czym muszą zostać uwzględnione opory wewnętrzne wszystkich ogniw. Musimy również uwzględnić opór galwanometru. Dla prądów związanych z szukaną siłą elektromotoryczną otrzymamy w oparciu o Prawa Kirchoffa; I_x=I_x1+I_x2 I_x(R_g+R_wx)+I_x1R_x1=U_x I_x2(R₂+R_w0)-I_x1R₁=0 Dla prądów wywołanych przez siłę elektromotoryczną U0 otrzymamy; I₀=I₀₁+I₀₂ I₀₂(R_g+R_wx)-I₀₁R₁=0 I₀(R₂+R_w0)+I₀₁R₁=U₀ Z układu podanych równań można znaleźć Ix1 i Ix2 w funkcji oporów i Ux , oraz I01 i I02 w funkcji tych samych oporów i U0 Z warunku znikania prądu w galwanometrze otrzymujemy

I₀₂=I_x U_x=R₁U₀/R_w0+R₁+R₂ Gdy Rw0 << R=R1+R2, metoda ta jest dokładna

.

28.Półprzewodniki(Rodzaje półprzewodników) Klasyfikując ciała pod względem właściwości elektrycznych bez względu na stan skupienia możemy podzielić je na trzy grupy: przewodniki, dielektryki i półprzewodniki. Półprzewodniki zajmują pośrednie miejsce między przewodnikami a dielektrykami. Podobnie jak w przypadku izolatorów najwyższe pasmo energetyczne zawierające elektrony tak zwane pasmo walencyjne jest całkowicie zapełnione ale tym razem przerwa energetyczna E_g między ostatnim pasmem zapełnionym i następnym dozwolonym jest mała. Dzięki temu małe dawki energii związane np. z ogrzaniem, naświetleniem itp. wystarczają do przeniesienia elektronów z pasma walencyjnego do pasma wyższego zwanego pasmem przewodnictwa. Rodzaje półprzewodników Znamy następujące typy półprzewodników:1)samoistne-chemicznie czyste(bezdomieszkowe) kryształy takie jak german, krzem. W temperaturze różnej od zera bezwzględnego część elektronów z pasma walencyjnego przechodzi do pasma przewodnictwa, które częściowo zapełnione elektronami może przewodzić prąd elektronowy. Ponadto po przejściu elektronów z pasma walencyjnego do pasma przewodnictwa w paśmie tym pozostają puste miejsca, zwane dziurami, które również biorą udział w przewodzeniu prądu elektrycznego, tworząc tzw. prąd dziurowy. Charakterystyczne cechy półprzewodników samoistnych:1.półprzewodnik samoistny w temp. zera bezwzględnego jest idealnym izolatorem.2. przewodność elektryczna półprzewodnika samoistnego ma charakter aktywacyjny, tzn. może być wywołana czynnikami takimi jak: temperatura, promieniowanie, silne pole elektryczne i innymi, które są w stanie udzielić elektronowi energii większej od E_g. 2)domieszkowe z domieszką donorów nazywane półprzewodnikami typu n - w strukturę pierwiastka IV grupy układu okresowego wprowadza się śladowe ilości pierwiastka z V grupy, którego piąty elektron walencyjny nie bierze udziału w wiązaniu. Elektron ten jest słabo związany i niewielka energia umożliwia mu przejście do pasma przewodnictwa. Poziom Fermiego jest położony powyżej środka przerwy energetycznej. Liczba elektronów swobodnych jest większa od liczby dziur. Atom domieszki nazywamy donorem. Półprzewodniki domieszkowe typu n charakteryzują się przewodnictwem elektronowym. Domieszki stanowią źródło elektronów przewodnictwa i noszą nazwę donorów, a powstałe dodatkowe poziomy energetyczne leżące w pobliżu pasma przewodnictwa, noszą nazwę poziomów donorowych. 3)półprzewodniki domieszkowe z domieszką akceptorów nazywane półprzewodnikami typu p- w strukturę pierwiastka IV grupy układu okresowego wprowadza się śladowe ilości pierwiastka z III grupy, którego trzy elektrony biorą udział w wiązaniu, natomiast miejsce czwartego uzupełnia jeden z elektronów związanych. W paśmie walencyjnym powstaje dziura. Liczba dziur jest większa od liczby swobodnych elektronów. Atom domieszki nazywamy akceptorem. Wprowadzenie domieszki powoduje obniżenie poziomu Fermiego. W półprzewodnikach domieszkowych typu p z domieszkami akceptorowymi powstaje dodatkowy poziom energetyczny akceptorowy E_a leżący bardzo blisko pasma walencyjnego. W wyniku przechodzenia elektronów z pasma walencyjnego na poziom akceptorowy w paśmie tym powstają dziury, dlatego też przewodnictwo elektryczne półprzewodników typu p ma charakter dziurowy. 4) półprzewodniki domieszkowe typu mieszanego(p i n)-znalazły szerokie praktyczne zastosowanie w elektronice półprzewodnikowej. Mają one równocześnie cechy półprzewodników typu n i p. Położenie poziomu Fermiego E_F zależy od temp. oraz koncentracji n_a- akceptorów i n_d- donorów. Jeżeli n_a<n_d to poziom Fermiego przesuwa się w kierunku poziomu akceptorowego, gdy zaś n_a>n_d to przesuwa się on w kierunku poziomu donorowego. Gdy n_a=n_d występuje równowaga i poziom E_F leży w środku szerokości pasma wzbronionego E_g

29.Siła Lorentza Siła oddziaływania pola magnetycznego na cząstkę naładowaną nosi nazwę siły Lorentza i wyraża się wzorem F_L^→=qv^→×B^→ gdzie q-ładunek, v^→-wektor jej prędkości, B^→-wektor indukcji pola magnetycznego. Siła Lorenza jest prostopadła zarówno do wektora prędkości jak i wektor indukcji, jej zwrot jest zgodny z kierunkiem posuwania się śruby prawoskrętnej podczas obracania jej od wektora v^→ do wektora B^→ . Wartość siły Lorentza określona jest wzorem F_L=qvBsinα gdzie α jest katem pomiędzy wektorami v ^→ i B^→. Siła osiąga maksymalna wartość, gdy oba wektory są prostopadłe. Wartość wektora indukcji jest definiowana jako stosunek maksymalnej siły działającej na cząstkę w polu magnetycznym do jej ładunku i prędkości. Jednostką indukcji jest tesla B=F_Lmax/qv [T=kg/As²] .Wektor indukcji jest w każdym punkcie styczny do linii pola magnetycznego. Gdy cząstka porusza się równolegle do linii pola magnetycznego, nie działa na nią siła. W przypadku, gdy prędkość jest prostopadła do linii pola siła ma maksymalną wartość, a torem ruchu jest okrąg. Funkcje siły dośrodkowej pełni siła Lorentza.

30.Prawo Gaussa dla pola magnetycznego Stwierdzony przez nas fakt, że linie pola magnetycznego są zawsze krzywymi zamkniętymi jest ściśle związany z faktem nieistnienia w przyrodzie ładunków magnetycznych analogicznych do ładunków elektrycznych. Wiąże się z tym następująca różnica miedzy własnościami pola elektrycznego i magnetycznego. Ja wiemy linii pola elektrycznego zaczynają się na ładunkach dodatnich, a kończą na ładunkach ujemnych. Jeżeli zatem otoczymy ładunek elektryczny dodatni zamkniętą powierzchnią to linie pola elektrycznego będą przebijać te powierzchnię na zewnątrz zgodnie z kierunkiem normalnej do powierzchni i strumień elektryczny przez te powierzchnię będzie równy wielkości ładunku znajdującego się wewnątrz powierzchni. W przypadku pola magnetycznego sytuacja jest inna. Linie indukcji magnetycznej są krzywymi zamkniętymi, zatem dowolną powierzchnię zamkniętą obejmującą biegun magnetyczny będzie przebijać zawsze jednakowa liczba linii indukcji wchodzących w wychodzących. Stad tez prawo Gaussa dla pola magnetycznego ma postać ∫pow BdS=0 czyli Strumień indukcji magnetycznej przez dowolna powierzchnię zamknięta jest równy zeru.

31.Prawo Biota Savarta Jeżeli prąd płynie przez przewodnik o bardziej skomplikowanym kształcie, natężenia pola magnetycznego nie można obliczyć na podstawie prawa Ampere'a. W tych przypadkach korzystamy z prawa Biota Savarta. Przypuśćmy, że mamy przewodnik o dowolnym kształcie, przez który płynie prąd I. Natężenie pola magnetycznego H w dowolnym punkcie P można obliczyć jako sumę elementarnych natężeń dH wytworzonych przez skierowane zgodnie z kierunkiem prądu elementy długości przewodnika dl, korzystając z prawa Biota Savarta dH=Idl×r/4πr³ przy czym r jest wektorem łączącym element dl z punktem P. Bezwzględna wartość elementarnego natężenia pola można wyrazić wzorem dH=Idlsinφ/4πr² Jak widać dH jest odwrotnie proporcjonalne do kwadratu odległości. Aby obliczyć natężenie pola wywołane działaniem całego przewodnika, należy scałkować równanie po wszystkich elementach dl tego przewodnika H=∫dH=I/4π∫dl×r/r³ Elementarny odcinek długości dl^→ przewodnika, w którym płynie prąd o natężeniu I wytwarza w próżni pole magnetyczne, którego indukcję dB^→ w punkcie P odległym o r^→ od elementu dl^→ opisuje prawo Biota Savarta dB^→=μ₀Idl^→×r^→/4πr³ dH^→=Idl^→×r^→/4πr³

32.Prawo Ampera Krążenie wektora indukcji magnetycznej po dowolnej krzywej zamkniętej L, obejmującej zbiór przewodników z prądem w próżni jest proporcjonalne do sumy algebraicznej natężeń prądów obejmowanych przez te krzywą

μ₀-przenikalność magnetyczna próżni μ₀=4π*10^-7 Vs/Am prawo Ampera: Cyrkulacja wektora natężenia pola magnetycznego jest równa sumie algebraicznej natężeń prądów płynących wewnątrz konturu całkowania.

---