Wahadło różnicowe

Opis metody pomiaru przyśpieszenia ziemskiego

Do wyznaczenia przyśpieszenia ziemskiego używaliśmy wahadła różnicowego, mierząc okresy wahadła przy różnej długości nici. Ponieważ okres drgań wahadła matematycznego wyraża się wzorem:

T= 2π

przyśpieszenie ziemskie obliczyć można dysponując danym okresem drgań wahadła i długością nici.

Wyniki pomiarów:

numer pomiaru	x [m]	t [s]	n	T [s]
	0,195	72,0	50	1,440
	0,180	70,4	50	1,408
	0,160	69,4	50	1,388
	0,140	68,2	50	1,364
	0,120	66,8	50	1,336
	0,100	65,0	50	1,300
	0,070	62,4	50	1,248
	0,040	60,2	50	1,204
	0,020	58,8	50	1,176
	0,005	57,0	50	1,140

Obliczenia.

Dla różnych zmian długości wahadła d_i = | x_k - x_i | obliczono przyśpieszenie ziemskie według wzoru gi = 4π²
, gdzie indeksy (k, l) odpowiadają numerom pomiarów. Obliczenia wykonano dla następujących zestawień indeksów (k, l): (1, 3), (1, 4), (1, 5), (2, 4), (2, 5), (3, 5)

Uzyskane wyniki:

g₁ = 9,396 m/s²

g₂ = 10,189 m/s²

g₃ = 10,256 m/s²

g₄ = 12,947 m/s²

g₅ = 11,989 m/s²

g₆ = 11,148 m/s²

Średnią wartość przyśpieszenia ziemskiego
obliczyliśmy ze wzoru:
=

i wyniosła ona
= 10,987 m/s².

Rachunek błędów.

Bezwzględny błąd przyśpieszenia ziemskiego wyliczyliśmy ze wzoru
=

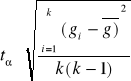
przy założonym
= 0,95 i k = 6. Jego wartość liczbowa wyniosła
= 1,308 m/s²

Wyniki końcowe

Uzyskany wynik wartości przyśpieszenia ziemskiego można przedstawić w postaci:

g = 10,987 * 1,308 m/s²

g = 9,679 ÷ 12,295 m/s²

Dyskusja wyników i błędów.

Otrzymany wynik po uwzględnieniu błędu jest zgodny z ogólnie znaną wartością przyśpieszenia ziemskiego, wynoszącą 9,81 m/s². Na wynik niewątpliwie wpłynąć mogły błędy podczas wykonywania pomiarów. Nieoczekiwane szturchnięcia staywu lub błęđy w liczeniu ilości wahnięć mogły spowodować przypadkowe błędy w pomiarze okresu wahadła. Z kolei niedokładność wskazań stopera lub przymiaru służącego do określenia długości nici oraz czas reakcji przy włączaniu lub zatrzymywaniu stopera mogły spowodować systematyczne błędy wpływające na dokładność wyznaczonego przyśpieszenia ziemskiego. Również, mimo iż drgania wahadła odbywały się dla niewielkich kątów (mniejszych od 7^o), należy pamiętać, iż nić na której zawieszona była kula wahadła posiada pewną masę i rozciągliwość, oraz że wahadło wykonywało ruchy nie tylko w płaszczyżnie poziomej, a więć badany model był jedynie przeybliżeniem idealnego wahadła matematycznego, do którego zastosowanie ma wzór T= 2π

1

---