Materiały pomocnicze do ćwiczeń laboratoryjnych z przedmiotu

Sygnały i Systemy Dynamiczne.

Ćwiczenie 1.

Analiza stanów dynamicznych systemów LTI z wykorzystaniem narzędzi środowiska programistycznego Matlab.

Problemy programistyczne (dla Matlaba 5.3)

1. Jak rozwiązać równanie różniczkowe zwyczajne I-go rzędu?

2. Jak rozwiązać równanie stanu?

3. Jak rozwiązać liniowe równanie różniczkowe zwyczajne n-tego rzędu?

Jeśli nie dysponujemy Symbolic Math Toolbox, problem 1 i 2 możemy rozwiązać graficznie za pomocą doskonałego pakietu numerycznych procedur rozwiązywania zagadnienia początkowego (zbiór funkcji ode). W przypadku 3 możliwe jest jedynie wykonanie zastosowanie przekształcenia Laplace'a (prostego i odwrotnego). Proste musi być wykonane ręcznie, odwrotne natomiast opiera się na rozkładzie funkcji F(s)=L(s)/M(s) na ułamki proste. Ponieważ liniowe równanie różniczkowe I-go rzędu traktować można jako szczególny przypadek liniowego równania stanu (układu równań różniczkowych I-go rzędu), oba te zagadnienia zostaną opisane w jednym podrozdziale.

I. Rozwiązywanie układu równań różniczkowych.

a. Wprowadzenie równania (definicja układu równań).

Równanie można zdefiniować (i tak jest najlepiej) w oddzielnym pliku `nazwa'.m

Przykład.1

Rozpatrzmy równania Van der Pola [1] zapisane w postaci normalnej równań stanu:

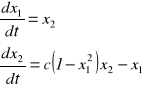
(1)

gdzie c jest współczynnikiem rzeczywistym (warunki początkowe: x₁(0)=0, x₂(0)=0.9). .

Plik funkcyjny (np. rvdp.m) definiujący wektor pochodnych zmiennych stanu
powinien wyglądać tak:

%Plik funkcyjny z definicją równania stanu van der Pola

function dx = rvdp(t,x)

%Wybór wartości stałej

c=1.5;

%Wektorowy zapis równania stanu: x(1),x(2)-> elementy wektora stanu

% dx -> wektor pochodnych zmiennych stanu.

dx = [x(2);

c*(1-x(1)*x(1))*x(2)-x(1)];

b. Rozwiązanie równania .

Do rozwiązania tak zdefiniowanego równania stanu stosuje się funkcję z rodziny ode o następującej znormalizowanej postaci:

SKŁADNIA

[t,x] = solver('F',zakres,x0)

[t,x] = solver('F',zakres ,x0,options)

[t,x] = solver('F',zakres,x0,options,p1,p2...)

F	Nazwa pliku ODE będącego funkcją MATLABa (względem t oraz x) wyświetlającą („zwracającą”) wektor. Wszystkie procedury ode rozwiązują równanie stanu o postaci , procedury typu: ode15s, ode23s, ode23t, ode23tb mogą rozwiązać równanie .
zakres	To wektor określający przedział całkowania [t0 tfinal].
x0	Wektor warunków początkowych.
options	Zestaw opcjonalnych parametrów procedur całkowania numerycznego definiowany funkcją odeset.
p1,p2...	Zestaw opcjonalnych parametrów do przekazania funkcji F.
solver	Nazwa wybranej procedury typu ode

Dostępne w naszej wersji Matlaka procedury całkowania numerycznego:

Solver	Problem	Dokładność	Kiedy stosować?
ode45	Nonstiff	Średnia	Do wszystkich zagadnień, pierwszy wybór.
ode23	Nonstiff	Mała	Tam gdzie możemy zadowolić się małą dokładności lub rozwiązując „średnio sztywne” problemy.
ode113	Nonstiff	Od małej do dużej	Gdy wymagana rygorystyczna tolerancja, duży nakład obliczeńIf
ode15s	Stiff	Od małej do średniej	Jeśli ode45 jest za wolna lub mamy do czynienia z macierzą M.
ode23s	Stiff	Mała	Gdy tolerancja może być duża i gdy macierz M jest stała.
ode23t	Moderately Stiff	Mała	Dla środniosztywnych problemów i obliczeń numerycznych bez silnie tłumionych przebiegów.
ode23tb	Stiff	Mała	Tam gdzie nie wymagamy dużej dokładności w obliczeniach układów “sztywnych” lub tam gdzie występuje macierz M.

Stiff Równania sztywne (zróżnicowane wartości pierwiastków równania charakterystycznego)

NonstiffRównania niesztywne (porównywalne wartości pierwiastków równania charakterystycznego).

Najprostszy m-plik zawierający rozwiązanie (graficzne) równania Van der Pola może mieć postać:

%Procedura główna rozwiązania równania Van der Pola zdefiniowanego w pliku 'rvdp'

%Warunki początkowe:

x0=[0; 0.9];

%Przedział całkowania:

zakres=[0 50]

%Procedura rozwiązująca równanie:

[t,x] = ode45('rvdp',zakres,x0);

%Wydruk ekranowy

subplot(2,1,1),plot(t,x(:,1),'-'),grid,xlabel('t'),ylabel('x1')

subplot(2,1,2),plot(t,x(:,2),'-'),grid,xlabel('t'),ylabel('x2')

Efekt działania powyższej procedury:

II. Rozwiązywanie równań różniczkowych zwyczajnych n-tego rzędu.

Ze względu na ograniczone możliwości dostępnej wersji Matlaba (brak narzędzi do analizy symbolicznej Symbolic Math Toolbox) wykorzystamy jedynie dostępne procedury rozkładu funkcji wymiernej na ułamki proste. Koncepcję metody wyjaśnimy na prostym przykładzie.

Przykład.2

Rozwiązać równanie różniczkowe (niejednorodne liniowe o stałych współczynnikach):

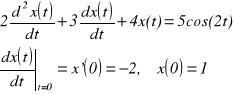
(2)

Rozwiązanie:

Stosując przekształcenie Laplace'a do równania (2) otrzymujemy:

(3)

Z równania (3) wyznaczamy funkcję wymierną X(s):

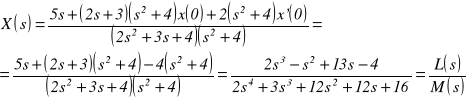
(4)

Funkcję wymierną X(s) można rozłożyć na ułamki proste za pomocą funkcji residue:

Syntax (Składnia)

[r,p,k] = residue(L,M)

Argumenty

L,M	Wektory zawierające współczynniki wielomianów uporządkowane w kolejności malejących potęg s
r	Wektor kolumnowy residuów
p	Wektor kolumnowy zer
k	Wektor wierszowy składników bezpośrednich (gdy stopień licznika jest >= od stopnia mianownika)

Gdy wielomian reszty (k) jest pusty, funkcję wymierną (4) można zapisać w postaci:

(4)

Wówczas transformatę odwrotną Laplace'a można przedstawić jako

(5)

Uwaga: Stosowalność wzoru (5) ograniczona jest do biegunów jednokrotnych! (powyższa procedura wymaga wówczas modyfikacji).

Przykładowy plik zawierający rozwiązanie równania (2):

%Rozwiązanie za pomocą Transformaty Laplace'a

L=[2 -1 13 -4];

M=[2 3 12 12 16];

t=[0:0.1:20];

[r,p,k]=residue(L,M);

u=0;

for i=1:length(r)

u=u+r(i)*exp(t.*p(i));

end

plot(t,u),grid,xlabel('t'),ylabel('x(t)')

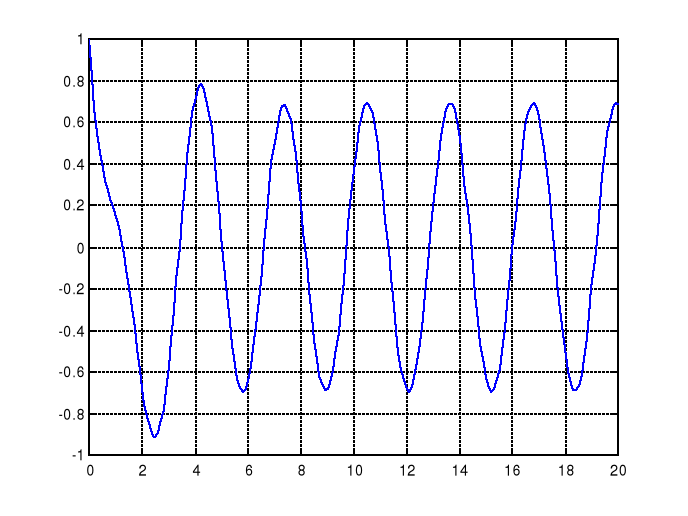
1

---