x
Nazwisko i Imię: Woźniak Piotr |
Wydział : MiIM / IV |
Grupa: 3 |
Temat: Rentgenowska analiza strukturalna. |
Data: 26.05.1999 |
Ocena: |
Cel ćwiczenia:
Celem ćwiczenia jest zapoznanie się z metodami badań opartymi na zjawiskach towarzyszących oddziaływaniu promieniowania rentgenowskiego lub neutronowego z materiałami w stanie krystalicznym.
Do rentgenowskich badań strukturalnych wykorzystuje się promieniowanie rentgenowskie w zakresie 0,01 do 10 mikrometra. Źródłem promieni rentgenowskich jest lampa rentgenowska zbudowana z katody i anody. Katoda wysyła elektrony które są przyspieszane do energii kilkudziesięciu keV i są kierowane na anodę wykonaną z miedzi, wolframu, chromu.
W wyniku oddziaływania rozpędzonych elektronów w polu elektrycznym z materiałem anody w lampach powstaje promieniowanie rentgenowskie. Składa się ono z:
widma ciągłego (białego, zwanego również widmem hamowania),
widma charakterystycznego ( zwanego również widmem linowym).
Ad a)
Widmo ciągłe powstaje na skutek hamowania elektronów pierwotnych rozpędzonych w polu elektrycznym i przemiany ich energii w energię fali elektromagnetycznej zgodnie ze wzorem:
ΔE=hν
ΔE- zmiana energii elektronów pierwotnych
h- stała Plancka
ν- częstotliwość powstającej fali.
Widmo ciągłe jest promieniowaniem nie mającym ściśle określonej długości fali ale zawiera fale z całego zakresu długości powyżej minimalnej wartości zwanej krótkofalową granicą widma (λKGW). Fala o minimalnej długości powstaje gdy elektron pierwotny w wyniku zderzenia z anodą całkowicie utraci swoją energię.
Ad b)
Powstaje ono w wyniku zmiany energii towarzyszącej ich przeskokom pomiędzy powłokami w atomach materiału anody. Przeskoki te są spowodowane wybijaniem elektronów z powłok elektronowych przez elektrony pierwotne oraz zajmowaniem ich miejsc przez elektrony z powłok elektronowych o wyższej energii czemu towarzyszy emisja energii w postaci fali elektromagnetyczej.
W przeciwieństwie do widma ciągłego, ma ono ściśle określone długości fali zwanych liniami charakterystycznymi. Długości te zależą od budowy atomów materiału z jakiego wykonana jest anoda lampy rentgenowskiej. Na anody stosuje się najczęściej: chrom, żelazo, kobalt, miedź, molibden (pierwiastki ułożone od największej do najmniejszej wartości λKαśr).
Oddziaływanie promieniowania rentgenowskiego z materią.
Rejestrowanie i analiza efektów oddziaływania promienia rentgenowskiego z materią pozwala na określenie zarówno składu chemicznego i składu fazowego jak i badania struktury krystalicznej materiałów, a także obserwacje radiologiczne. Metody opierają się na analizie zjawisk towarzyszących temu oddziaływaniu którymi są :
absorpcja - natężenie promieniowania przy przejściu przez materię słabnie ze wzorem:
J=J0exp(-μ/ρ*ρ*x)
J0 - natężenie wiązki padającej
J - natężenie wiązki po przejściu przez warstwę materii o grubości x
μ/ρ - masowy współczynnik absorpcji
ρ - gęstość materiału przez który przechodzi wiązka promieniowania
x
I0 I
próbka
fluorescencja - czyli emitowanie przez materię własnego charakterystycznego promieniowania rentgenowskiego wzbudzonego przez promieniowanie pierwotne ( padające).
dyfrakcja - czyli spójne rozproszenie promieniowania na atomach ciała krystalicznego oraz jego interferencja (wzmocnienie). Warunkiem zajścia dyfrakcji jest spełnienie prawa Bragga opisanego wzorem:
nλ=2dhklsinθ jest to warunek wzmocnienia fali ugiętej na płaszczyznach kryształu
n - rząd odbicia
λ - długość fali promieniowania rentgenowskiego
dhkl - odległość między płaszczyznami krystalograficznymi dhkl
θ - kąt odbłysku
Absorbcja:
Zadanie 1.
Obliczyć ilu krotnie ulega osłabieniu wiązka promieniowania rentgenowskiego lampy molibdenowej:
przechodząc przez warstwę 0,001 osłony ołowianej
przechodząc przez drogę 50 cm w powietrzu
Dane:
Masowy współczynnik. absorpcji :
- ołowiu dla promieniowania lampy molibdenowej μ/ρ= 141 [cm2/g]
- powietrza dla promieniowania lampy molibdenowej μ/ρ= 1,29 [cm2/g]
gęstość:
ołowiu ρ= 11,34 [cm3/g]
powietrza ρ=1,31*10-3 [cm3/g]
ad a)
dla ołowiu:
![]()
ad b)
dla powietrza:
![]()
Wnioski:
Wiązka promieniowania rentgenowskiego lampy molibdenowej przy przejściu prze ołów została zdecydowanie osłabiona, zaś przy przyjściu przez warstwę powietrza tylko nieznacznie. Wniosek z tego że ołów bardzo dobrze zatrzymuje promieniowanie rentgenowskie, dlatego jest stosowany jako tania osłona przy aparatach rentgenowskich.
Zadanie 2.
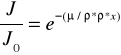
Oblicz grubość preparatu następujących pierwiastków : Li, C, Ni,Al, Pb które osłabiają promieniowanie molibdenu i chromu o 80%.
![]()
![]()
![]()
Tabela wyników:
|
Li |
C |
Al |
Pb |
Ni |
Rodz. promienio-wania |
|
0,22 |
0,7 |
5,3 |
141 |
47,4 |
Mo |
|
2,11 |
17,9 |
149 |
585 |
145 |
Cr |
ρ [g/cm3] |
0,53 |
2,22 |
2,7 |
11,34 |
8,9 |
Mo |
|
0,53 |
2,22 |
2,7 |
11,34 |
8,9 |
Cr |
μ [1/cm] |
0,116 |
1,554 |
14,3 |
1598,94 |
421,86 |
Mo |
|
1,118 |
39,738 |
402,3 |
6633,9 |
1290,5 |
Cr |
X [cm] |
13,88 |
0,044 |
0,11 |
0,001 |
0,004 |
Mo |
|
1,44 |
0,04 |
0,004 |
0,0002 |
0,012 |
Cr |
Wnioski:
Z pośród pięciu pierwiastków dla których liczyłem grubość zasłony przy której następował spadek promieniowania o 80% największą skutecznością okazał się ołów (x=0,004 cm dla Mo i x=0,012 cm dla Cr), zaś najmniejszą lit (x=13,88 cm dla Mo i x=1,44 cm dla Cr)
Zadanie 3
Jakościowa analiza fazowa
Metoda Debyea-Schererra.
Warunki pomiaru: promieniowanie - λKα1=1,542 A
Średnica kamery - D = 57,3 mm
2θ - 180°
Zdjęcie które otrzymałem ma długość równą 180mm.
Licząc od środków prostokątów odległość wynosi 92 mm.
Aby obliczyć ile stopni zawiera 1 mm układam proporcję:
92 mm -180°
1 mm - x°
x=1,96°
![]()
Numer prążka |
L [mm] |
2θ |
θ [°] |
sin θ |
dhkl |
1 |
21,5 |
42,14 |
21,07 |
0,359 |
2,147 |
2 |
25 |
49 |
24,5 |
0,414 |
1,862 |
3 |
32 |
62,72 |
31,36 |
0,52 |
1,482 |
4 |
45,5 |
89,18 |
44,59 |
0,702 |
1,1 |
5 |
47 |
92,12 |
46,06 |
0,720 |
1,07 |
6 |
59,5 |
116,62 |
58,31 |
0,851 |
0,9 |
7 |
69,5 |
136,22 |
68,11 |
0,928 |
0,83 |
8 |
73,5 |
144,06 |
72,03 |
0,951 |
0,81 |
Wnioski:
Na podstawie danych zawartych w tablicach i własnych obserwacji mogę przypuszczać, że zdjęcie które analizowałem jest zdjęciem srebra Ag . Wartości dhkl najbardziej były zbliżone do wartości wzorcowych tegoż metalu.
Zadanie 4.
Na podstawie zapisu dyfraktogrametrycznego określić materiał.
Promieniowanie - λ=1,79A
Numer piku |
2 θ [°] |
θ [°] |
sin θ |
dhkl |
Dhkl tabl. |
Faza |
|
1 |
38 |
19 |
0,32 |
2,79 |
2,75 |
Fe3W3C |
|
2 |
41,6 |
20,8 |
0,355 |
2,52 |
2,52 |
Fe3W3C |
|
3 |
43,5 |
21,75 |
0,37 |
2,42 |
2,4 |
VC |
|
4 |
46,8 |
23,4 |
0,397 |
2,25 |
2,249 |
Fe3W3C |
|
5 |
50 |
25 |
0,422 |
2,12 |
2,122 |
Fe3W3C |
|
6 |
50,9 |
25,45 |
0,429 |
2,08 |
2,07 |
Feα |
|
7 |
52,4 |
26,2 |
0,44 |
2,03 |
2,07 |
VC |
|
8 |
54,6 |
28,3 |
0,47 |
1,9 |
1,912 |
V8C7 |
|
9 |
59,5 |
29,75 |
0,49 |
1,82 |
1,819 |
V8C7 |
|
10 |
70,8 |
35,4 |
0,58 |
1,54 |
1,545 |
Fe3W3C |
|
11 |
77 |
38,5 |
0,62 |
1,44 |
1,44 |
Fe3W3C |
|
12 |
83,4 |
41,7 |
0,66 |
1,35 |
1,47 |
Fe3W3C |
|
13 |
86,8 |
43,4 |
0,68 |
1,31 |
1,30 |
Fe3W3C |
|
14 |
89 |
44,5 |
0,7 |
1,27 |
1,26 |
Feα |
|
Wnioski:
Osnową danego stopu i głównym składnikiem jest żelazo α (Feα) zaś wtrąceniami są węgliki: V8C7, WC, Fe3W3C, VC występujące w badanym stopie są charakterystyczne dla stali szybkotnącej.
![]()