Zad. 1 .

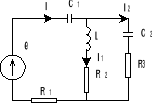
Obliczyć moce na R1, R2, R3, moc czynną i bierną układu , jeżeli:

L = 0,0637 H , C1=C2 = 159,24 μF , R1=R2=R3=R= 20 Ω, e= 282,85sinωt,

f= 50 Hz

Rozwiązanie.

ω = 2πf = 314

X_C = 1/ωC = 20 Ω

X_L = ωL = 20 Ω

E = 200 V

Z = R1 -jX_C1 + (R₃- jX_C2)(R₂+jX_L) / (2R+j(X_L-X_C)) = (40 - j20) Ω

I = 200V / (40 - j20) Ω = (4 + j2) A

Należy dokonać rozdziału prądu I na prądy gałęzi równoległych.

Zgodnie z działaniem „dzielnika prądu”

I₂ = (R₂ +jX_L) / (R₂ +jX_L - jX_C + R₃) = (1 + j3) A

I₁ = I - I₁ = (3 - j1) A

Moduły prądów i moce (wartości zaokrąglone)

I = 4,47 P_R1 = 400 W

I₁= 3,16 P_R2 = 200 W

I₂= 3,16 P_R3 = 200 W

S = E I^* = 200 (4-j2)

P= 800 W Q = 400 VAr

---