Filtr Kalmana
Filtr Kalmana możemy używać do nieliniowych systemów i dyskretnego modelu stanu. Filtracja Kalmana jest skuteczna dla wyznaczenia oceny parametrów modelu, z powodu dwoistości, jest również podobny do charakterystyki problemu LQR.
model liniowego nieustalonego procesu możemy matematycznie przedstawić jako:
![]()
gdzie ω(t) oznacza zmienną losową, wartość oczekiwaną zmiennej losowej wynosi:
![]()
gdzie ε(t) jest operatorem wartości oczekiwanej:
![]()
gdzie cov jest operatorem kowariancji
gdzie operator wartości oczekiwanej możemy zdefiniować jako:
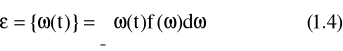
gdzie f(ω)jest funkcją gęstości prawdopodobieństwa. Kowariancja jest natomiast definiowana jako:
![]()
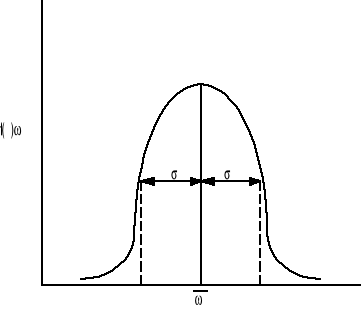
dla skalarnej zmiennej losowej ω, funkcja gęstości prawdopodobieństwa według rozkładu Gaussa wynosi:
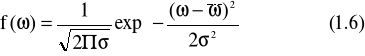
gdzie: σ2 - wariancją rozkładu,
pierwiastek kwadratowy σ2 wynosi σ i jest nazywany standardowym odchyleniem, ![]()
- średnia wartością i jest wartością oczekiwana rozkładu normalnego. Wykres rozkładu normalnego jest przedstawiony poniżej
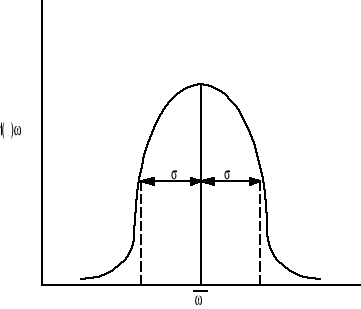
Rysunek ten przedstawia kształt rozkładu a także wartość średnią i odchylenie standardowe
Rys. Funkcja gęstości prawdopodobieństwa Gaussa.
Dla zmiennych wektorowych rozkład Gaussa wyraża się wzorem:
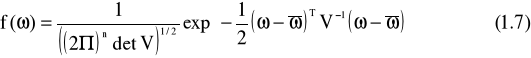
gdzie:
![]()
- wartość średnia określona wzorem
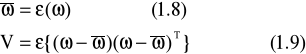
V - kowariancja macierzy określona wzorem
Warunki początkowe procesu są następujące:
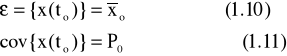
liniowy pomiar systemu jest modelowany następujący:
![]()
gdzie υ(t) jest szumem losowym:
dla którego przyjmuje się taki rozkład normalny że
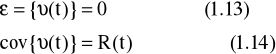
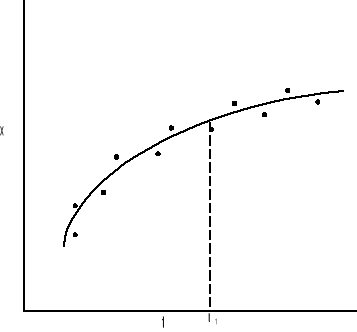
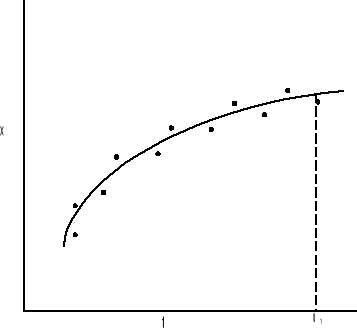
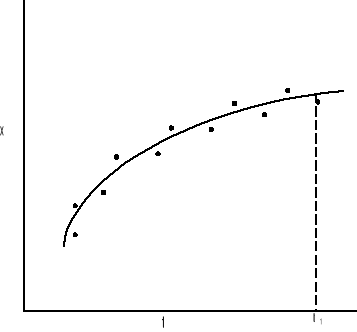
Jest kilka sposobów jak można użyć modelu probablistycznego i systemu pomiarowego. Te sposoby to: wygładzanie, filtrowanie i predykcja. Wygładzanie polega na użyciu danych przed i po czasie t1 do zapewnienia estymaty stanu dla czasu t1. Jest to proces niesekwencyjny i jest przedstawiony na rys:
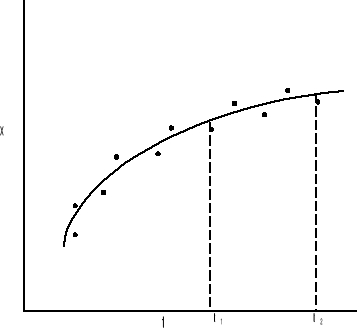
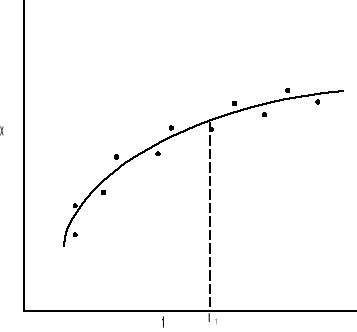
Filtrowanie jest estymatą stanu dla czasu t1 wówczas gdy użyte są wszystkie dane aż do czasu t1. Jest to proces sekwencyjny przedstawiony na rys:
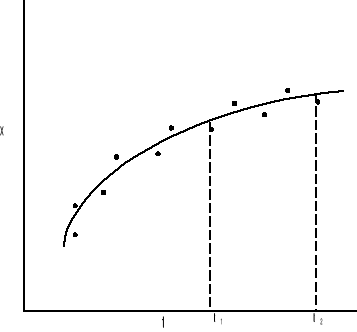
Predykcja jest uzyskiwaniem estymat stanu dla czasu t2 na podstawie danych do czasu t1 gdzie t1 jest mniejsze od t2.
Kalman rozważał uzyskanie optymalnej estymaty stanu procesu liniowego opisanego równaniem:
![]()
gdzie:
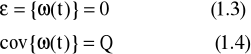
a warunki początkowe wynoszą:
![]()
gdzie:
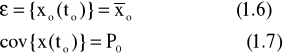
Wówczas model pomiarowy określony jest następująco:
![]()
gdzie:
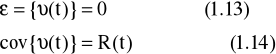
Chcemy znaleźć optymalną estymatę stanu, która minimalizuje funkcjonał:
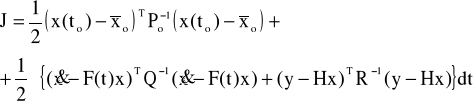
używając odwrócenia macierzy kowariancji w funkcjonale uzyskujemy bardziej dokładne stany i pomiary w procesie optymalizacji. Ten problem może być także sformułowany jako problem optymalnego sterowania przez zdefiniowanie wektora sterowania jako:
![]()
po przekształceniu równanie stanu wynosi:
![]()
a funkcjonał wynosi:
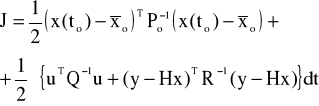
Hamiltonian dla tego problemu wynosi:
![]()
a warunki konieczne dla zminimalizowania funkcjonału jakości są następujące:
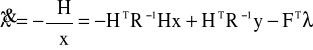
gdy x(0) jest równe zero otrzymamy
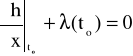
po przekształceniu:
![]()
lub
![]()
stan końcowy jest także wolny, co prowadzi do:
![]()
wówczas optymalne sterowanie wynosi:
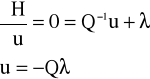
Weźmy pod uwagę zagadnienie filtracji, które określa optymalne estymaty dla czasu końcowego na podstawie znajomości danych aż do czasu końcowego. Oznaczmy optymalne estymaty dla czasu tk i dla danych y(t) do czasu tk wyznaczoną przy pomocy filtracji jako :
![]()
Wprowadzając transformację Riccatiego
![]()
chcemy określić funkcje z(t) i P(t), które są konsekwencją warunków koniecznych dla optymalizacji. Optymalna estymaty są określone przez model stanu i sterowanie optymalne jako:
![]()
Używając transformacji Riccatiego do oceny zarówno ![]()
otrzymamy:
![]()
albo korzystając z równania * otrzymamy:
![]()
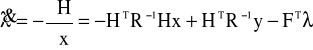
Przenosząc wszystkie z na lewą stronę równania i λ na prawą stronę otrzymamy:
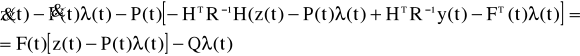
Zależność ta jest prawdziwa ⇔ gdy obie strony równania 10.2.28 są równe zero. Prowadzi to do następującej zależności:
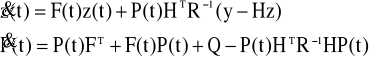
na podstawie początkowych warunków transwersalności równania 10.2.19 i transformacji Riccatiego otrzymamy:
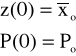
Oba warunki są dla czasu początkowego, dlatego powyższe równania są integralne w każdej następnej chwili czasu. Dla problemu filtracji próbujemy wyznaczyć
![]()
Jest to ostatni najmniejszy kwadratowa estymata dla czasu tk oparta na wszystkich danych aż do czasu tk . Końcowy warunek transwersalności jest następujący:
![]()
co oznacza że, na podstawie transformacji Riccatiego otrzymuje się:
![]()
Dlatego dla filtracji otrzymujemy:
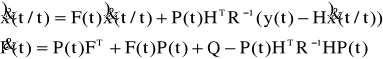
przy warunkach początkowych:
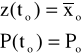
Równania 10.2.35 10.2.36 znane są jako filtr Kalmana, i zostały sformułowane po raz pierwszy przez Kalmana i Bucy'ego w 1961 roku.
Wzmocnienie filtra definiuje się jako:
![]()
Dla stanu końcowego równanie 10.2.36 przedstawia stan ustalony, więc wzmocnienie filtra dla stanu ustalonego wynosi:
![]()
a optymalne estymaty stanu są następujące:
![]()
Filtr Kalmana posiada kilka ważnych własności:
Odchylenie estymaty stanu.
Błąd estymaty stanu definiujemy jako:
![]()
Oczekiwaną wartość błędu definiuje się jako:
![]()
kowariancję błędu definiujemy jako:
![]()
dlatego macierz P(t) jest kowariancją bieżącego błędu i jest nazywana wariacją minimalnego błędu.
Wariancja ![]()
- charakteryzuje rozrzut wartości zmiennej losowej X wokół wartości średniej E(X). Niech X = (X1, X2, ... , Xn) zmienna losowa wielowymiarowa (weźmy dla prostoty r = 2) niech także:
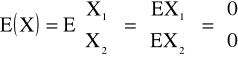
gdyby tak nie było możemy zmienną scentrować ![]()
czyli odjąć od niej wartość średnią.
Macierz kowariancji definiujemy:
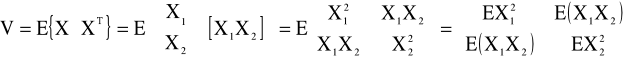
przy założeniu scentrowania mamy:
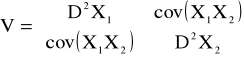
Wyszukiwarka
Podobne podstrony:
kalman filtr
Filtr (elektronika)
Kalman
Filtr paliwa seria K
Filtr p pylkowy 1154k
Filtr wody do c o
AudioAmp z trx TEN–TEC 580 Delta, schemat dxp filtr ssb i cw TC 580
Filtr cw sp5ww
Filtr Pakietow OpenBSD HOWTO id Nieznany
filtr komorowy
filtr kabinowy
filtr zraszający
Filtr Paliwa
Filtr aktywny
dodatkowy filtr scaf1
filtr hydroponiczny(1)
FILTR PALIWA OSADNIK POMPA ODPOWIETRZAJĄCA
więcej podobnych podstron