Politechnika Śląska
Wydział AEiI
Kierunek AiR
Ćwiczenia laboratoryjne z fizyki :
Badanie zjawiska Halla
Grupa I, sekcja 5
Lesław Kaczor
Andrzej Sikorski
Gliwice, 16.03.1994
1.Opis teoretyczny.
Zjawisko Halla polega na tym że, jeśli przez płytkę przewodnika (półprzewodnika) umieszczoną w polu magnetycznym B przepuści się prostopadle, do kierunku tego pola, prąd elektryczny, to w płytce wytwarza się poprzeczne pole elektryczne, prostopadłe do kierunku przepływu prądu i do kierunku pola magnetycznego. Zjawisko Halla powstaje na skutek odchylenia nośników prądu w polu magnetycznym pod wpływem siły Lorentza :
![]()
Zjawiskiem Halla nazywamy zjawisko galwanomagnetyczne polegające na pojawianiu się napięcia (tzw. napięcia Halla UH) w płytce półprzewodnika lub metalu, przez którą płynie prąd elektryczny i umieszczonej w polu magnetycznym. Pomiar napięcia Halla jest jedną z podstawowych metod badania właściwości nośników ładunku, zwłaszcza w półprzewodnikach. Na podstawie znaku napięcia Halla można określić jaki rodzaj nośników (dziury czy elektrony) dominuje w przewodnictwie. Pomiar temperaturowej zależności napięcia Halla oraz konduktancji w półprzewodniku umożliwia określenie właściwości domieszek (ich koncentracji, rodzaju, energii wiązania), mechanizmów rozpraszania nośników ładunku oraz dostarcza informacji o strukturze pasmowej półprzewodników.
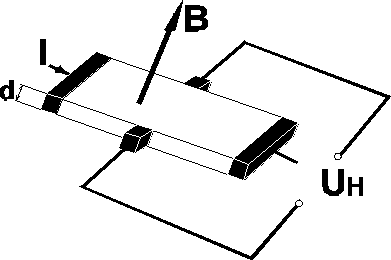
Na rysunku, pokazana jest płytka półprzewodnika, w której płynie prąd I, umieszczona w polu magnetycznym o indukcji B, prostopadłym do płaszczyzny płytki. Siły działające w polu magnetycznym na ładunki dodatnie i ujemne byłyby skierowane w tą samą stronę, gdyż ładunki te mają różne znaki, ale i jednocześnie różnie skierowane prędkości unoszenia (prędkości dryfu) VD W wyniku działania tych sił nośniki prądu niezależnie od tego czy są dodatnie czy ujemne będą odchylane w prawą (w tym przypadku) stronę. Przesunięcie tych ładunków spowoduje powstanie poprzecznego pola elektrycznego Halla EH, które przeciwstawia się dalszemu przesuwaniu ładunków w poprzek przewodnika. W stanie równowagi wypadkowa tych dwóch sił musi być równa zeru : ![]()
. Ponieważ gęstość prądu ![]()
, więc : ![]()
a napięcie Halla ![]()
gdzie d oznacza grubość płytki przewodnika. Iloraz ![]()
nazywamy współczynnikiem (stałą) Halla. Kierunek pola Halla jest różny dla różnych znaków nośników prądu, co pozwala na określenie typu nośników w konkretnych przewodnikach.
2.Opis ćwiczenia.
Ćwiczenie polegało na połączeniu obwodu pokazanego na schemacie i pomiarze napięcia Halla w zależności od prądu płynącego przez hallotron oraz od pola magnetycznego w którym się on znajdował. W tym celu zastosowano następującą kolejność postępowania :
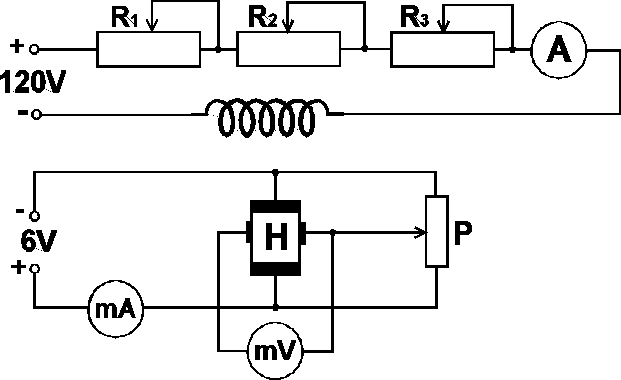
- przy wyłączonym obwodzie cewki nastawiano żądaną wartość prądu Is płynącego przez hallotron i kompensowano napięcie asymetrii,
- włączano prostownik i notowano wskazanie miliwoltomierza,
-wyłączano prostownik,
- ustalano nową wartość prądu Is , po czym cała procedura była powtarzana.
Charakterystyki hallotronu wyznaczano dla pięciu różnych pól magnetycznych cewki odpowiadających natężeniu prądu Ia = 3, 4 ,5 ,6 i,7 A.
3.Tabela pomiarowa.
miliamperomierz Is klasa 0.5
ilość działek 30
zakres 30 mA
amperomierz Ia dokładność odczytu 1/3 ost. dekady
zakres 10 A
miliwoltomierz dokładność odczytu 1/3 ost.dekady
Tabela pomiarowa
Is |
Napięcie Halla UH [mV] dla prądu Ia [A] |
||||
|
3 |
4 |
5 |
6 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0.7 |
1.0 |
1.1 |
1.4 |
1.7 |
4 |
1.4 |
1.9 |
2.3 |
2.8 |
3.5 |
6 |
2.2 |
2.8 |
3.4 |
4.3 |
5.2 |
8 |
3.0 |
3.9 |
4.4 |
5.7 |
6.9 |
10 |
3.6 |
4.7 |
5.5 |
7.0 |
8.1 |
12 |
4.4 |
5.6 |
6.7 |
8.4 |
9.6 |
14 |
5.1 |
6.7 |
7.7 |
9.8 |
11.2 |
16 |
5.8 |
7.7 |
8.9 |
11.3 |
12.7 |
18 |
6.5 |
8.4 |
10.0 |
12.7 |
14.5 |
20 |
7.2 |
9.3 |
11.1 |
13.8 |
15.8 |
22 |
7.9 |
10.3 |
12.1 |
15.2 |
17.2 |
24 |
8.6 |
11.2 |
13.0 |
16.5 |
18.8 |
26 |
9.2 |
11.9 |
14.1 |
17.8 |
20.0 |
4.Opracowanie wyników pomiarów.
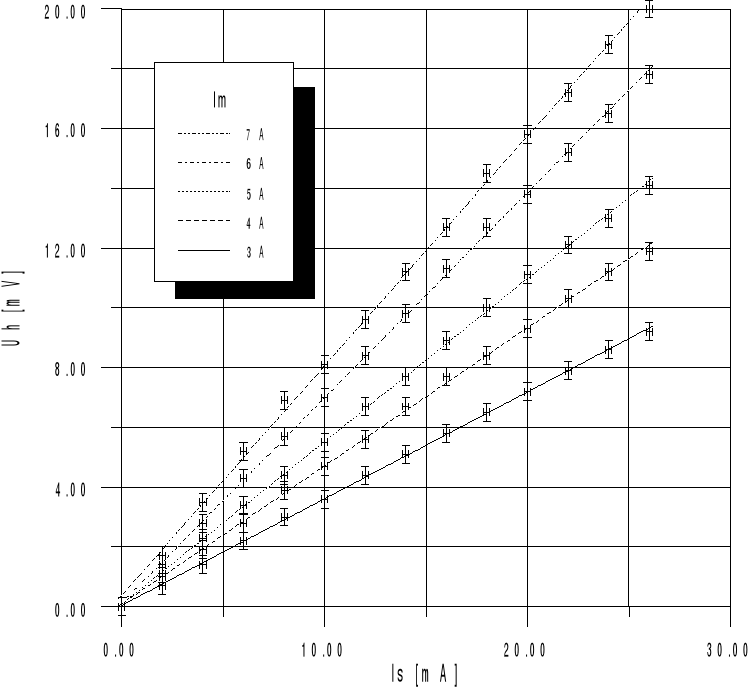
Analiza błędów.
Niepewność pomiarowa dla amperomierza Ia : ±0.03 A
Niepewność pomiarowa dla miliwoltomierza UH 0.3 mV
Wykres charakterystyk hallotronu
Niepewność pomiarowa dla miliamperomierza Is :
![]()
Metodą regresji liniowej obliczam współczynnik nachylenia charakterystyk a oraz jego błąd.
![]()
Następnie stałą hallotronu :
gdzie :
![]()
l = 0.95 m - długość solenoidu
n=1500 - liczba zwojów
![]()
Jej błąd względny liczymy z różniczki zupełnej:
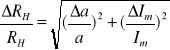
1) Im=3 A
UH= 0.357 Is
![]()
![]()
RH=59.96 ± 0.7 m2/C
2) Im=4 A
UH= 0.46 Is
![]()
![]()
RH=58.24 ± 0.63 m2/C
3) Im=5 A
UH= 0.54 Is
![]()
![]()
RH=54.89 ± 0.46 m2/C
4) Im=6 A
UH= 0.69 Is
![]()
![]()
RH=57.68 ± 0.44 m2/C
5) Im=7 A
UH= 0.768 Is
![]()
![]()
RH= 55.306± 0.57 m2/C
Obliczam średnią ważoną stałej hallotronu oraz jej błąd :
RHśr=56.86 ± 0.24 m2/C
Obliczam stałą Halla ze wzoru:
R=d*RH
gdzie d= 2 m - grubość użytego hallotronu
R=1.137*10-4 m3/C ± 0.42%
5 Podsumowanie.
Na wykresie wszystkie proste wyznaczone metoda regresji przechodzą przez krzyże błędów wszystkich punktów co świadczy o dużej dokładności pomiarów .Z tego można wnioskować, że stała Halla została wyznaczona z dużą dokładnością. Otrzymana stała Halla jest większa od zera, wynika z tego, że dominującym typem przewodnictwa w badanym hallotronie jest typ dziurowy, więc jest to półprzewodnik.
Wyszukiwarka
Podobne podstrony:
badania mikroskopowe zeliw, Politechnika Śląska Zarządzanie i Inżynieria Produkcji, Semestr 3, Mater
Badanie zjawisk dyfrakcyjnych, Politechnika ˙l˙ska Studia Wieczorowe
BADANIE PRZETWORNIKA HALLA, POLITECHNIKA ŚWIĘTOKRZYSKA, POLITECHNIKA ŚWIĘTOKRZYSKA
Badanie szeregowego rezonansu napięciowego, Badanie szeregowego rezonansu napięciowego 5, Politechni
Ściąga na kolosa z wykładu, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Sem
Badanie szeregowego rezonansu napięciowego, Badanie szeregowego rezonansu napięciowego 4, Politechni
BADANIE WYTRZYMAŁOSCI POWIETRZA PRZY NAPIĘCIU PRZEMIENNYM, Politechnika Śląska, Wydział Elektryczny,
sedno, Politechnika śląska - Mechatronika semestr 1 i 2, Podstawy Nauki o materiałach, laborki, ćw 1
notatka, Politechnika śląska - Mechatronika semestr 1 i 2, Podstawy Nauki o materiałach, laborki, ćw
wszystko w tym temacie, Politechnika śląska - Mechatronika semestr 1 i 2, Podstawy Nauki o materiała
Badania Politechnika Slaska id 76150 (2)
badanie wybranych właściwości oleju, Politechnika Śląska, Wydział Elektryczny, Semestr 3, Inżynieria
Badanie wytrzymałości elektrycznej skrośnej wybranych materiałów izolacyjnych stałych (Politechnika
Badanie materialow ferromagnetycznych, Politechnika ?l?ska______Studia Wieczorowe
Badanie prądnicy synchronicznej, POLITECHNIKA RADOMSKA
Badanie prądnicy tachometrycznej, Badanie prądnicy tachometrycznej, POLITECHNIKA RADOMSKA
spr nr 4 Efekt Halla, efekt halla, Politechnika Warszawska
więcej podobnych podstron