Piotr Pawłowicz 162960

Olga Serwinie 162973

• Wydział Chemiczny Politechniki Wrocławskiej

• Laboratorium z Elektrotechniki i Elektroniki

Pomiar rezystancji (omomierz). Mostek niezrównoważony

1. Cel ćwiczenia.

Celem ćwiczenia jest poznanie zasady działania mostka Wheatsone'a do pomiaru rezystancji oraz jego właściwościami w zastosowaniach jako mostek zrównoważony i wychyłowy.

2. Spis przyrządów pomiarowych.

• Multimetr Metex M-4640A, ΔU±0.05rdg+3dgt.

• Opornik dekadowy.

• Makieta mostka rezystancji.

3. Schematy pomiarowe.

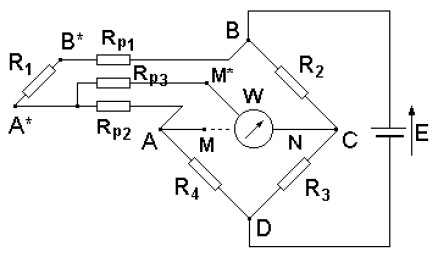
Rys.1. Schemat mostka Wheatsone'a do pomiaru rezystancji.

Legenda:

E- SEM źródła.

R_z- rezystancja wewnętrzna źródła.

W- wskaźnik zrównoważenia mostka.

R_w- rezystancja wewnetrzna wskaźnika.

Legenda:

E- SEM źródła.

R_z- rezystancja wewnętrzna źródła.

W- wskaźnik zrównoważenia mostka.

R_w- rezystancja wewnetrzna wskaźnika

Rys. 2. Mostek rezystancyjny z trójprzewodowym połączeniem mierzonego napiecia.

4. Tabele pomiarowe.

5.1.2

R2	R3	R4	Rx=R1	ΔR1[%]
481	100	100	481	3,13
474	1000	100	47	3,08

Przykładowe obliczenia.

Np. 1%+0.5%+0.5%+1%+0.13%=3.13[%].

Np. 1%+0.5%+0.5%+0.5%+0.3%=3.08[%].

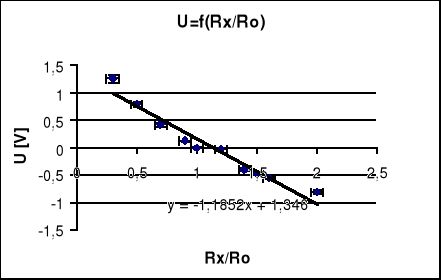
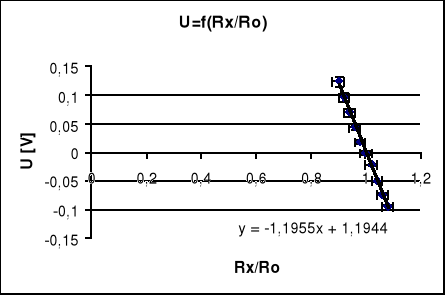
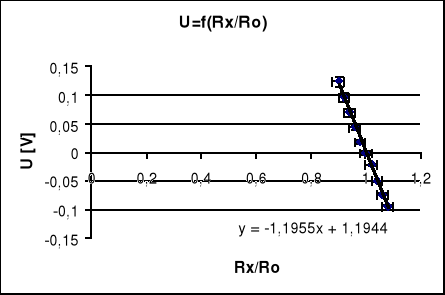
5.1.3 Wartości mierzone przy R₂=100Ω R₃=R₄=100Ω czyli stosunku R₄/ R₃=1 przy U=5[V]

zmierzonym za pomocą miernika cyfrowego i wynoszącym U=5.067[V].Przy równomiernie zmieniającym się stosunku Rx/Ro w granicach 0.2÷2.0 oraz 0.9÷1.1 gdzie Ro jest wartością rezystancji R_xw stanie równowagi.

Lp.	Rx [Ω]	Rx/Ro	U [V]	ΔU[V]	U± ΔU[V]
1.	30	0,3	1,261	0,066	1,261±0,066
2.	50	0,5	0,786	0,042	0,786±0,042
3.	70	0,7	0,415	0,024	0,415±0,024
4.	90	0,9	0,121	0,009	0,121±0,009
5.	100	1	-0,001	0,003	-0,001± 0,003
6.	120	1,2	-0,022	0,002	-0,022±0,002
7.	140	1,4	-0,404	0,017	-0,404±0,017
8.	150	1,5	-0,484	0,021	-0,484±0,021
9.	160	1,6	-0,559	0,025	-0,559±0,025
10.	200	2	-0,808	0,037	-0,808±0,037

Lp.	Rx [Ω]	Rx/Ro	U [V]	ΔU[V]	U± ΔU[V]
1.	90	0,90	0,124	0,009	0,124±0,009
2.	92	0,92	0,097	0,008	0,097±0,008
3.	94	0,94	0,070	0,007	0,070±0,007
4.	96	0,96	0,045	0,005	0,045±0,005
5.	98	0,98	0,019	0,004	0,019±0,004
6.	100	1,00	-0,001	0,003	-0,001±0,003
7.	102	1,02	-0,021	0,002	-0,021±0,002
8.	104	1,04	-0,050	0,001	-0,050±0,001
9.	106	1,06	-0,073	0,001	-0,073±0,001
10.	108	1,08	-0,086	0,001	-0,086±0,001
11.	110	1,10	-0,118	0,003	-0,118±0,003

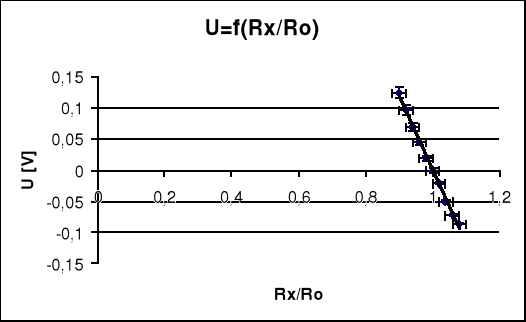
Rx- rezystancja dla mostka w stanie równowagi.

U- napięcie mierzone Multimetrem.

ΔU- niepewność bezwzględna dla przyrządu cyfrowego.

R_o -jest wartością rezystancji

Przykładowe obliczenia:

ΔU=0.05*1,261+3*0.001=0,066 [V].

U± ΔU=1,261±0,066 [V].

Rx/Ro=30[Ω]/100[Ω]= 0,3

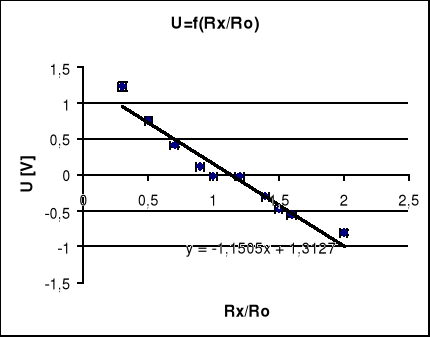
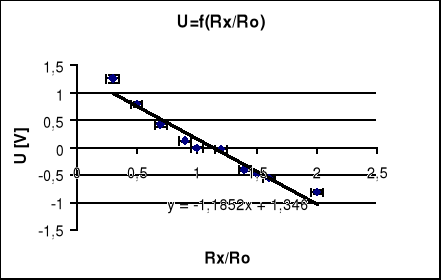
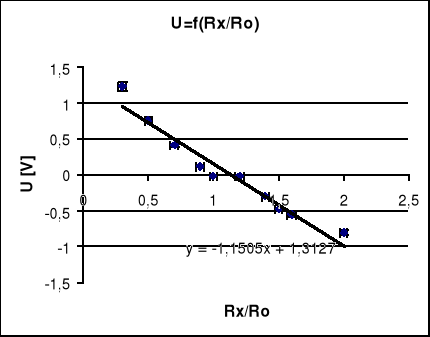
5.1.4 Wartości mierzone przy R₂=100Ω R₃=R₄=1kΩ czyli stosunku R₄/ R₃=1przy U=5[V]

zmierzonym za pomocą miernika cyfrowego i wynoszącym U=5.067[V].Przy równomiernie zmieniającym się stosunku Rx/Ro w granicach 0.2÷2.0 oraz 0.9÷1.1 gdzie Ro jest wartością rezystancji R_xw stanie równowagi.

Lp.	Rx [Ω]	Rx/Ro	U [V]	ΔU[V]	U± ΔU[V]
1.	30	0,3	1,231	0,065	1,231±0,065
2.	50	0,5	0,762	0,041	0,762±0,041
3.	70	0,7	0,410	0,024	0,410±0,024
4.	90	0,9	0,112	0,009	0,112±0,009
5.	100	1	-0,010	0,003	-0,010±0,003
6.	120	1,2	-0,021	0,002	-0,021±0,002
7.	140	1,4	-0,304	0,012	-0,304±0,012
8.	150	1,5	-0,474	0,021	-0,474±0,021
9.	160	1,6	-0,548	0,024	-0,548±0,024
10.	200	2	-0,802	0,037	-0,802±0,037

Lp.	Rx [Ω]	Rx/Ro	U [V]	ΔU[V]	U± ΔU[V]
1.	90	0,90	0,123	0,009	0,123±0,009
2.	92	0,92	0,096	0,008	0,096±0,008
3.	94	0,94	0,069	0,007	0,069±0,006
4.	96	0,96	0,043	0,005	0,043±0,005
5.	98	0,98	0,018	0,004	0,018±0,004
6.	100	1,00	-0,001	0,003	-0,001±0,003
7.	102	1,02	-0,022	0,002	-0,022±0,002
8.	104	1,04	-0,050	0,001	-0,050±0,001
9.	106	1,06	-0,073	0,001	-0,073±0,001
10.	108	1,08	-0,094	0,001	-0,074±0,001
11.	110	1,10	-0,112	0,003	-0,112±0,003

Rx- rezystancja dla mostka w stanie równowagi.

U- napięcie mierzone Multimetrem.

ΔU- niepewność bezwzględna dla przyrządu cyfrowego.

R_o -jest wartością rezystancji

Przykładowe obliczenia:

ΔU=0.05*1,231+3*0.001=0,065 [V].

U± ΔU=1,231±0,065 [V].

Rx/Ro=90[Ω]/100[Ω]= 0,90

6. Wnioski.

Cel ćwiczenia został osiągnięty. Mostek Wheatstone'a jest szeroko stosowany w czujnikach pomiarowych, ze względu na możliwość kompensowania wpływu przewodów na element pomiarowy. Stosuje się go także do pomiaru rezystancji. Na podstawie wniosków z ćwiczenia pierwszego, doszedłem do wniosków, że mostek jest w stanie równowagi, odchylenie od wartości 0 spowodowane jest błędem wskazania woltomierza cyfrowego. Wielokrotne powtarzanie pomiarów dało takie same wyniki. W punkcie drugim sprawdziłem przydatność mostków do pomiarów rezystancji. Dobierając rezystory R₃ i R₄ można uzyskać skalowanie rezystancji mierzonej. Wzór ogólny prostej dołączony do wszystkich wykresów umożliwia położenie dalszych punktów

---