ANALIZA REGRESJI I KORELACJI

1. Estymacja i test istotności dla współczynnika korelacji

Przy badaniu populacji generalnej równocześnie ze względu na dwie lub więcej cech mierzalnych posługujemy się pojęciami regresji i korelacji. Korelacja zajmuje się siłą tej zależności, a regresja - jej kształtem. Po ustaleniu, że między badanymi cechami istnieje niezbyt słaba korelacja, przystępuje się do znalezienia funkcji regresji, która pozwala na przewidywanie wartości jednej cechy przy założeniu, że druga cecha przyjęła określoną wartość.

Gdy zależność między dwiema badanymi cechami jest linowa, to najlepszym miernikiem korelacji między nimi jest tzw. współczynnik korelacji ρ który definiujemy:

gdzie cov(X,Y) oznacza kowariancje X i Y . Współczynnik korelacji jest miarą korelacji, bo
.

Gdy p= - 1 lub p= + 1, wtedy między zmiennymi X i Y istnieje ścisła zależność w postaci funkcji liniowej. Gdy p=0, wtedy zmienne są nieskorelowane. Im |p| jest bliższa 1, tym korelacja jest mocniejsza.

Estymatorem zgodnym współczynnika korelacji ρ między dwiema badanymi cechami X i Y w populacji jest współczynnik korelacji z próby, który oznaczamy zwykle symbolem r i obliczamy z n par (x_i, y_i) wyników próby według wzoru:

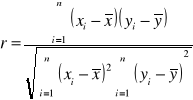
Rozkład estymatora r parametru p jest na ogół dla dowolnych rozkładów populacji bardzo skomplikowany. Przy założeniu, ze populacja generalna ma dwuwymiarowy rozkład normalny z parametrem ρ=0, rozkład współczynnika korelacji z próby r jest prosty i sprowadza się do rozkładu t Studenta.

Gdy próba jest bardzo duża, można też skorzystać z granicznego rozkładu normalnego. Pozwala to na zbudowanie przedziału ufności oraz na sprawdzenie hipotezy dla wartości współczynnika korelacji ρ w populacji.

Model I

Dwuwymiarowy rozkład badanych dwu mierzalnych cech X i Y w populacji generalnej jest normalny bądź zbliżony do normalnego. Z populacji tej wylosowano do próby dużą liczbę elementów (n- kilkaset) by na podstawie wyników tej próby oszacować współczynnik korelacji ρ. Przybliżony wzór na przedział ufności dla ρ jest wtedy następujący:

,

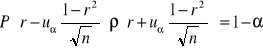
gdzie
jest wartością standaryzowanej zmiennej normalnej odczytaną z tablicy rozkładu N(0,1), dla ustalonego z góry współczynnika ufności 1-α, w taki sposób, by P{-u_α < U< u_α }= 1-α. Ze względu na dużą próbę wygodnie jest wtedy wyniki jej pogrupować w postaci tzw. tablicy korelacyjnej, z której obliczamy r według wzoru

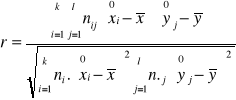
gdzie
jest środkiem poszczególnego przedziału klasowego zmiennej X (w tablicy jest k takich przedziałów),
jest środkiem poszczególnego przedziału klasowego zmiennej Y (w tablicy jest l takich przedziałów), n_ij jest liczebnością dla poszczególnej kratki tablicy, a n_i. oraz n._j są liczebnościami brzegowymi w tablicy korelacyjnej.

Model II

Dwuwymiarowy rozkład badanych cech X i Y w populacji generalnej jest normalny lub zbliżony do normalnego. Z populacji tej wylosowano (niekoniecznie dużą) próbę n elementową. Na podstawie wyników tej próby należy sprawdzić hipotezę, że zmienne X i Y nie są skorelowane, tzn. hipotezę H₀: ρ=0, wobec hipotezy alternatywnej H₁: ρ
0.

Test istotności dla tej hipotezy jest następujący. Obliczamy wartość współczynnika korelacji r z próby oraz wartość statystyki

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ rozkład t Studenta z n-2 stopniami swobody. Z tablicy rozkładu t Studenta dla ustalonego z góry poziomu istotności α i dla n-2 stopni swobody odczytujemy wartość krytyczną t_α tak, by P{|t|
t_α }=α.

Przykład

Dokonano n=500 niezależnych pomiarów pewnych dwu wymiarów losowych. odlewów i otrzymano z tej próby r=0,82. Przyjmując współczynnik ufności 1-α=0,95 zbudować przedział ufności dla nieznanego współczynnika korelacji ρ między dwoma wymiarami.

Rozwiązanie

Można przyjąć, że dwuwymiarowy rozkład wymiarów odlewów jest normalny. Ze względu na dużą próbę można przedział ufności dla ρ wyznaczyć według wzoru w modelu I. Mamy zatem

, 1-r²=0,3276

Z tablicy rozkładu N(0, 1) odczytujemy wartość u_α=1,96. Przedział ufności dla ρ ma więc końce

czyli

0,82-0,029<ρ<0,82+0,029, skąd 0,791< ρ<0,849.

Przykład 2

Spośród studentów pewnego wydziału uczelni wylosowano niezależnie 10 studentów IV roku i otrzymano dla nich następujące średnie oceny uzyskane w sesji egzaminacyjnej na I roku studiów (x_i) oraz na IV roku studiów (y_i):

xi	3,5 4,0 3,8 4,6 3,9 3,0 3,5 3,9 4,5 4,1
yi	4,2 3,9 3,8 4,5 4,2 3,4 3,8 3,9 4,6 4,0

Na poziomie istotności α=0,05 zweryfikować hipotezę, że istnieje korelacja między wynikami studiów uzyskiwanymi przez studentów tego wydziału na I i IV roku.

Rozwiązanie

Z punktu widzenia formalnego stawiamy hipotezę H₀: ρ=0, wobec hipotezy alternatywnej H₁: ρ≠0, i weryfikujemy ją za pomocą testu istotności dla modelu II. Obliczenie współczynnika korelacji z próby r przeprowadzamy w formie tabelarycznej wykorzystując wygodny wzór

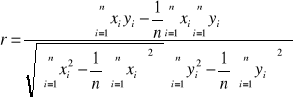
i	xi	yi			xiyi
1 2 3 4 5 6 7 8 9 10	3,5 4,0 3,8 4,6 3,9 3,0 3,5 3,9 4,5 4,1	4,2 3,9 3,8 4,5 4,2 3,4 3,8 3,9 4,6 4,0	12,25 16,00 14,44 21,16 15,21 9,00 12,25 15,21 20,25 16,81	17,64 15,21 14,44 20,25 17,64 11,56 14,44 15,21 21,16 16,00	15,70 15,60 14,44 20,70 16,38 10,20 13,30 15,21 20,70 16,40
	38,8	40,3	152,58	163,55	157,63

Stąd

,

Otrzymujemy zatem

Obliczamy teraz wartość statystyki

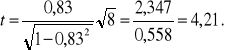
Dla przyjętego poziomu istotności α=0,05 odczytujemy z tablicy rozkładu t Studenta przy 8 stopniach swobody krytyczną wartość t_α=2,306. Ponieważ |t|=4,21>2,306= t_α, zatem hipotezę H₀ należy odrzucić. Oznacza to, że dodatni współczynnik korelacji między wynikami uzyskiwanymi przez studentów tego wydziału na I i IV roku różni się istotnie od zera.

Współczynnik determinacji d = rur x 100 w %

d- 0,69 --- 69 %

Wyniki egzaminów osiągane prez studentów na pierwszym roku determinują wyniki osiągane na roku IV w około 69%

2. Estymacja liniowej funkcji regresji

Przy badaniu zależności między różnymi cechami mierzalnymi w populacji generalnej używa się wygodnego pojęcia funkcji regresji. W statystyce rozróżnia się dwa rodzaje regresji, mianowicie pierwszego i drugiego rodzaju.

Funkcję regresji pierwszego rodzaju definiuje się jako wartość oczekiwaną warunkowego rozkładu jednej zmiennej, gdy druga zmienna przyjmuje ustalone wartości.

Funkcja regresji drugiego rodzaju jest to taka funkcja określonego typu, której parametry zostały wyznaczone metodą najmniejszych kwadratów dla zaobserwowanych w próbie wartości badanych zmiennych. Gdy badanie dotyczy dwu cech, to można mówić o dwu funkcjach regresji Y względem X lub X względem Y.

Liniowa funkcja regresji występuje najczęściej w praktyce. Gdy tylko mamy prawo twierdzić, że dwuwymiarowy rozkład X i Y jest normalny lub zbliżony do normalnego, to funkcję regresji drugiego rodzaju traktujemy jako funkcję liniową o równaniu y=αx+β.

Metoda najmniejszych kwadratów dla liniowej funkcji regresji polega na takim oszacowaniu parametrów α i β, aby dla danych z próby n wartości (x_i, y_i) osiągnęła najmniejszą wartość funkcja S, określona wzorem

Prowadzi to, po zastosowaniu warunku koniecznego i dostatecznego na istnienie minimum funkcji dwu zmiennych, do układu dwóch równań liniowych, którego rozwiązanie daje szukane oszacowanie parametrów α i β. Parametr α nosi nazwę współczynnika regresji Y względem X i wyraża średnią zmianę wartości Y, gdy X zmieniła wartość o jedną jednostkę.

Model

Dwuwymiarowy rozkład badanych dwóch cech mierzalnych X i Y w populacji generalnej jest normalny bądź zbliżony do normalnego. Z populacji tej wylosowano do próby n elementów i otrzymano dla tych cech wyniki (x_i, y_i) (i=1, 2, ..., n). Na podstawie wyników próby należy oszacować parametry liniowej funkcji regresji y=αx+β.

Metoda najmniejszych kwadratów daje następujące oszacowanie prostej regresji

,

gdzie a i b wyznacza się z próby według wzorów:

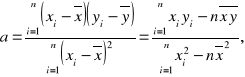
Estymatory a i b są nieobciążonymi i zgodnymi estymatorami parametrów α i β. Obszar ufności dla prostej regresji y=αx+β ograniczony tzw. krzywymi ufności, wyznacza się według wzoru

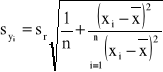
Przykład

Badając zależność między wielkością produkcji X pewnego wyrobu a zużyciem Y pewnego surowca zużywanego w produkcji tego wyrobu otrzymano dla losowej próby n=7 obserwacji następujące wyniki (x_i w tys. sztuk, y_i w tonach):

xi	1 2 3 4 5 6 7
yi	8 13 14 17 18 20 22

Należy przy współczynniku ufności 0,95 oszacować metodą przedziałową zarówno całą liniową funkcję regresji, jak i sam współczynnik regresji zużycia surowca względem wielkości produkcji.

Rozwiązanie

Nanosząc otrzymane punkty empiryczne na wykres stwierdzamy, że badaną regresję można przyjąć za liniową. Estymację liniowej funkcji regresji przeprowadzimy według wzorów z modelu I. Wartości estymatorów a i b wyznaczamy metodą najmniejszych kwadratów.

xi	yi
1 2 3 4 5 6 7	8 13 14 17 18 20 22	-3 -2 -1 0 1 2 3	-8 -3 -2 1 2 4 6	24 6 2 0 2 8 18	9 4 1 0 1 4 9	9,5 11,7 16,0 13,8 18,1 20,2 22,4	2,25 1,69 0,04 1,00 0,01 0,04 0,16
28	112			60	28		5,19

Stąd

Otrzymujemy zatem oszacowanie prostej regresji
.Wartości
tej funkcji liniowej oraz kwadraty ich odchyleń od empirycznych wartości y_i obliczamy w tej samej tabelce. Mamy

skąd

Dla n-2=5 i dla przyjętego współczynnika ufności 0,95 otrzymujemy z tablicy rozkładu t Studenta wartość t_γ=2,571. Ponadto mamy

Wartości
oraz rzędne punktów leżących na krzywych ufności wygod­nie jest również obliczyć tabelarycznie. Mamy

xi
1 2 3 4 5 6 7	9,5 11,7 13,8 16,0 18,1 20,2 22,4	9 4 1 0 1 4 9	0,321 0,143 0,036 0 0,036 0,143 0,321	0,464 0,286 0,179 0,143 0,179 0,286 0,464	0,681 0,535 0,423 0,378 0,423 0,535 0,681	0,695 0,546 0,431 0,386 0,431 0,546 0,695	1,8 1,4 1,1 1,0 1,1 1,4 1,8	7,7 10,3 12,7 15,0 17,0 18,8 20,6	11,3 13,1 14,9 17,0 19,2 21,6 24,2
		28

Przedział ufności dla współczynnika regresji α otrzymujemy ze wzoru

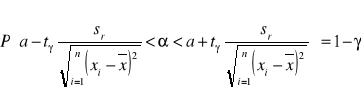
Mamy

a=2,14, t_γ=2,571, s_r=1,02 oraz

Przedział ufności dla współczynnika regresji α jest więc następujący:

skąd

Przykład 3 Metoda uproszczonego algorytmu

Obliczyć współczynnik regresji i korelacji liniowej oraz narysować prostą regresji dla ustalenia zależności pomiędzy liczbą asortymentów wyrobów produkowanych przez poszczególne przedsiębiorstwa i osiąganych przez nie wartości sprzedaży w tys. zł.

i	xi	yi tyś zł			xiyi
1	25	180	625	32 400	4 500
2	55	320	3 025	102 400	17 600
3	82	700	6 724	490 000	57 400
4	185	900	34 225	810 000	166 500
5	68	200	4 624	40 000	13 600
6	250	1 320	62 500	1 742 400	330 000
7	125	750	15 625	562 500	93 750
8	95	700	9 025	490 000	66 500
9	350	2 500	122 500	6 250 000	875 000
10	290	1 500	84 100	2 250 000	435 000
11	650	3 500	422 500	12 250 000	2 275 000
12	320	2 200	102 400	4 840 000	704 000
13	122	600	14 884	360 000	73 200
14	180	850	32 400	722 500	153 000
15	225	950	50 625	902 500	213 750
16	60	500	3 600	250 000	30 000
17	195	1 100	38 025	1 210 000	214 500
Σ	3 277	18 770	1 007 407	33 304 700	5 723 300
Σx * Σy	61 509 290

Kolejno obliczamy poprawki c_x, c_y i c_xy

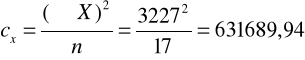
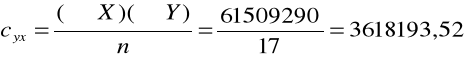
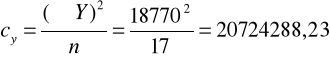
Kolejno obliczamy sumę kwadratów odchyleń dla x, dla y oraz dla xy.

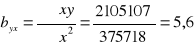
Otrzymana wartość współczynnika regresji b_yx = 5,6 oznacza, że wraz ze wzrostem liczby asortymentów produkowanych o 1 wartość rocznej sprzedaży przedsiębiorstwa wzrasta o 5 600 zł.

Na podstawie wartości współczynnika regresji oraz wartości średniej

X_sr = 192,76 i y _sr = 1104,12

Wyznaczamy równanie prostej regresji na podstawie kanonicznej postaci równania prostej

= b_yx (
)

Y - 1104,12 = 5,6(x - 192,76)

Y =1104,12 + 5,6x - 1079,46

Y =5,6x + 24,66 - jest to równanie prostej regresji

Na podstawie równania prostej regresji możemy narysować wykres równania regresji tworząc układ współrzędnych z osiami x i y oraz obliczenie wartości y z równania regresji liniowej dla wartości x₁ = 100 i x₂ =400

Y₁ =( 5,6 x 100) - 24,66 =535,34

Y₂ = (5,6 x 400) - 24,66 = 2215,34

Kolejno obliczamy współczynnik korelacji

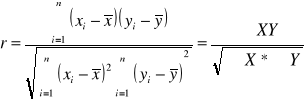
Kolejno obliczamy współczynnik determinacji d, który jest kwadratem współczynnika korelacji.

d= r²

d=0,968²=0,937

Wartość współczynnika determinacji pomnożona przez 100 wyraża nam procent zmienności zmiennej zależnej objaśnianej przez wartość zmiennej niezależnej. W tym przypadku możemy stwierdzić, że liczba produkowanych przez przedsiębiorstwo wyrobów w 93,7 % decyduje o wartości rocznej sprzedaży wyrobów.

\

Przykład 4

W tablicy 4 przedstawiono liczbę firm komputerowych tworzonych w poszczególnych latach w woj. kujawsko-pomorskim w okresie lat 1990 -2009. Na podstawie zawartych w tablicy danych oblicz współczynnik regresji, korelacji i determinacji a z kanonicznej postaci równania prostej wyznacz prostą regresji na podstawie której opracuj prognozę ilości firm komputerowych przewidywanych do rejestracji w roku 2012 i w latach 2014 oraz w 2015

Tablica 4 zestawienie danych dla obliczeń z zadania 4

i	xi	yi = r-1989			xiyi
1	379	1
2	438	2
3	423	3
4	479	4
5	564	5
6	557	6
7	634	7
8	683	8
9	758	9
10	823	10
11	812	11
12	945	12
13	843	13
14	932	14
15	1054	15
16	985	16
17	1089	17
18	957	18
19	1168	19

Wykonaj obliczenia dla zawartych w tablicy 4 danych według wzorów przedstawionych w przykładzie 3 oraz prognozy wyliczone dla lat wg wzoru na uproszczoną wartość zmiennej zależnej np. Y ₂₀₁₂= Y₂₂

---