Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej |
||||||||
Imię i nazwisko: Daniel Romanowski
|
Grupa: ED 3.5 |
|||||||
Data wykonania: 1998.11.09
|
Ćwiczenie nr: 6.1
|
Temat zadania: Pomiar grubości cienkich warstw metodą interferencji. |
||||||
Zaliczenie: |
Ocena: |
Data: |
Podpis |
|||||
Cel ćwiczenia:
Zapoznanie się z pomiarami mikronierówności powierzchni przy pomocy mikroiterferometru Linnika.
Zazwyczaj do mierzenia grubości materiału używamy suwmiarki, śruby mikrometrycznej, lecz mierzą one wielkości rzędu 10-2 -10-4 m. Mniejszych wielkości nie jesteśmy w stanie mierzyć metodami mechanicznymi. By dokonać pomiaru takich wielkości, wykorzystuje się w pracowniach fizycznych tzw. mikroskopy interferencyjne. Zasadę działania tego typu mikroskopu ilustruje poniższy rysunek:
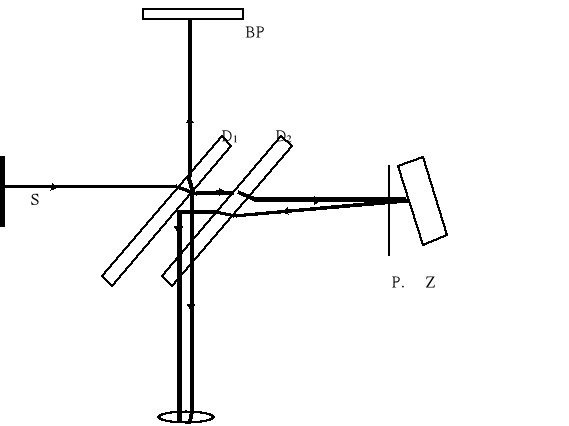
na którym: BP-powierzchnia badana,
D1,D2-płytki płaskorównoległe,
Z-zwierciadło,
S-wiązka światła.
Wiązka światła S pada na płytkę płaskorównoległą D1, pokrytą z jednej strony cienką warstwą srebra i dzieli się na dwie wiązki: przechodzącą i odbitą. Pierwsza z nich pada dalej na płytkę D2 i po odbiciu się od zwierciadła Z wraca, ulega odbiciu na płytce D1 i wpada do układu rejestrującego. Druga wiązka pada na badaną powierzchnię i po odbiciu się od niej dostaje się także do okularu. Obie wiązki interferują ze sobą dając obraz interferencyjny badanej powierzchni.
Mikroskop taki jest wstanie zmierzyć wielkości rzędu 10-6 ÷ 10-8 m. Oczywiście w okularze nie widzimy badanego materiału. Widzimy natomiast obraz powstały w wyniku nałożenia się na siebie spójnych fal świetlnych. W skutek czego powstają minima i maksima natężenia światła, widoczne jako podłużne ciemne i jasne prążki. Gdy materiał ma nieregularną powierzchnię, wówczas następuje przesunięcie Δx. Przesunięcie to jest ściśle związane z wielkością skoku h.
Prążki interferencyjne uzyskiwane pod mikroskopem przedstawia rysunek:
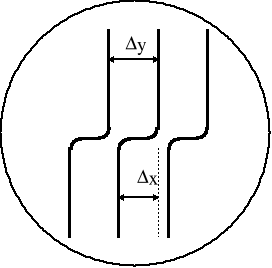
Zmianę grubości badanej płytki można wtedy wyznaczyć z zależności:
![]()
Wykonanie ćwiczenia:
Po uzyskaniu obrazu interferencyjnego zmierzyłem zarówno odległość między prążkami niezdeformowanymi Δy, jak i wielkość przesunięcia prążka Δy. Do pomiarów wykorzystałem prążki ciemne ze względu na lepszy kontrast. Odczytu położenia obserwowanego prążka dokonywałem nastawiając śrubę mikrometryczną okularu tak, by niż krzyża przechodziła dokładnie przez jego środek. Położenie prążka określała zarówno działka widziana w świetle okularu jak i jej setne części odczytane z bębna okularu. Dla próbki wykonałem 20 pomiarów , wykorzystując do pomiarów światło białe.
Wyniki pomiarów zanotowałem w poniższej tabeli:
Lp. |
ΔX [dz.] |
ΔXśr [dz.] |
rx [dz.] |
r x 2 [dz.2] |
ΔY [dz.] |
ΔYśr [dz.] |
ry [dz.] |
ry2 [dz.2] |
1 |
35 |
35,15 |
0,15 |
0,0225 |
22 |
18,4 |
-3,6 |
12,96 |
2 |
36 |
|
-0,85 |
0,7225 |
18 |
|
0,4 |
0,16 |
3 |
38 |
|
-2,85 |
8,1225 |
15 |
|
3,4 |
11,56 |
4 |
37 |
|
-1,85 |
3,4225 |
17 |
|
1,4 |
1,96 |
5 |
35 |
|
0,15 |
0,0225 |
16 |
|
2,4 |
5,76 |
6 |
38 |
|
-2,85 |
8,1225 |
17 |
|
1,4 |
1,96 |
7 |
38 |
|
-2,85 |
8,1225 |
16 |
|
2,4 |
5,76 |
8 |
37 |
|
-1,85 |
3,4225 |
18 |
|
0,4 |
0,16 |
9 |
36 |
|
-0,85 |
0,7225 |
18 |
|
0,4 |
0,16 |
10 |
33 |
|
2,15 |
4,6225 |
23 |
|
-4,6 |
21,16 |
11 |
34 |
|
1,15 |
1,3225 |
20 |
|
-1,6 |
2,56 |
12 |
36 |
|
-0,85 |
0,7225 |
18 |
|
0,4 |
0,16 |
13 |
34 |
|
1,15 |
1,3225 |
16 |
|
2,4 |
5,76 |
14 |
34 |
|
1,15 |
1,3225 |
18 |
|
0,4 |
0,16 |
15 |
37 |
|
-1,85 |
3,4225 |
16 |
|
2,4 |
5,76 |
16 |
31 |
|
4,15 |
17,223 |
20 |
|
-1,6 |
2,56 |
17 |
36 |
|
-0,85 |
0,7225 |
19 |
|
-0,6 |
0,36 |
18 |
35 |
|
0,15 |
0,0225 |
20 |
|
-1,6 |
2,56 |
19 |
33 |
|
2,15 |
4,6225 |
21 |
|
-2,6 |
6,76 |
20 |
37 |
|
-1,85 |
3,4225 |
20 |
|
-1,6 |
2,56 |
Wartości obliczone w tabeli wyznaczyłem ze wzorów:
rx = ΔXśr - ΔX ry = ΔYśr - ΔY
np.
rx = ΔXśr - ΔX = 35,15 - 35 = 0,15 dz.sk. ry = ΔYśr - ΔY = 18,4 - 22 = -3,6 dz.sk
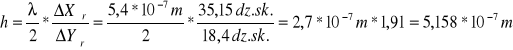
Na podstawie wartości średnich obliczyłem wartość średnią pomiaru skoku h:
![]()
Dyskusja błędu:
Dyskusję błędu przeprowadzam metodą Gaussa, stosując przy tym kryterium trójsigmowe:
-dyskusja wielkości ΔX
Obliczam średni błąd kwadratowy pojedynczego pomiaru:
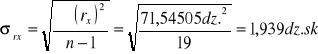
Ponieważ żaden pomiar nie jest obarczony błędem większym niż 3σ, więc obliczam średni błąd kwadratowy średniej arytmetycznej:
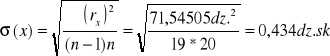
-dyskusja wielkości ΔY
Obliczam średni błąd kwadratowy pojedynczego pomiaru:
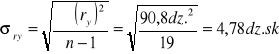
Ponieważ pomiary spełniają kryterium trójsigmowe, więc obliczam średni błąd kwadratowy średniej arytmetycznej:
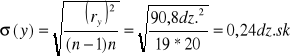
Błąd wielkości wyznaczonej h obliczam ze wzoru:
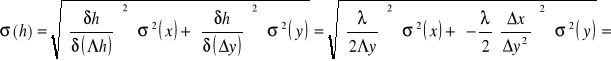
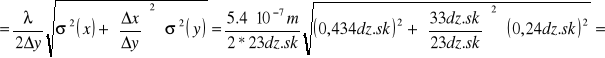
= 6,5 * 10-9 m
Błąd względny procentowy pomiaru h wynosi zatem:
![]()
Błąd pomiaru jest niezwykle mały, co może być wynikiem wykonania dokładnych pomiarów lub pomyłki w obliczeniach.
![]()
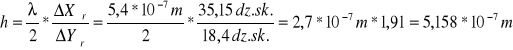
![]()
Wyszukiwarka
Podobne podstrony:
79 1111 1124 The Performance of Spray Formed Tool Steels in Comparison to Conventional
MULTIKONTO AQUARIUS Z KREDYTEM 02964484 1124[1]
1124
1124
1124
(6101) zbiory przyblizoneid 1124 ppt
1124
1124 dziesięć przykazań ?jm NJ2TC4NMVDKWNJZKJVQX5EI2WDSDNB46GHVI3LQ
MULTIKONTO AQUARIUS Z KREDYTEM 02964484 1124[1]
tsd 1124
Nalkowska Zofia Medaliony (SCAN dal 1124)
Nalkowska Zofia Medaliony (SCAN dal 1124)
1124
1124 Brandenburgisches Konzert Nr 6 partytura
1124 Cacadores Da Arca Perdida (Muzyka z filmu INDIANA JONES ) partytura
ROBO 1124 elektronika
więcej podobnych podstron