Pole elektryczne przepływowe prądu stałego:
Zad1. Dany jest kondensator kulisty o R1 i R2, konduktywności izolacji, do którego doprowadzono napięcie U. Obliczyć rezystancję izolacji R, prąd upływu I oraz moc P wydzieloną na izolacji kondensatora.
![]()
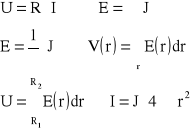
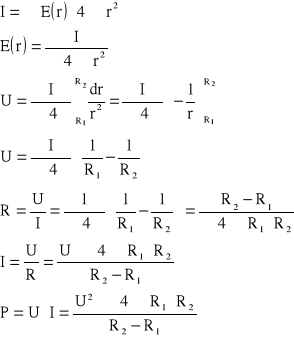
Zad2. Dany jest kondensator kulisty uwarstwiony szeregowo, R1 - wewn. R3 - zewn, R2 - promień powierzchni sferycznej oddzielającej obie warstwy dielektryka. Obliczyć: R, U, I, P.
rezystancję izolacji R, prąd upływu I oraz moc P wydzieloną na izolacji kondensatora.
![]()
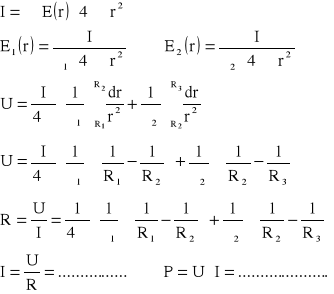
Zad3. Izolacja kabla koncentrycznego ma konduktywność 5∙10-9 S/m. Napięcie między żyłą wewnętrzną a powłoką kabla wynosi U=5kV, promień żyły wewn R1=10mm, promień wewn powłoki R2=40mm. Obliczyć rezystancję izolacji odcinka kabla o długości l=1km, prąd upływu oraz moc strat.
![]()
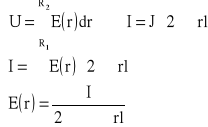
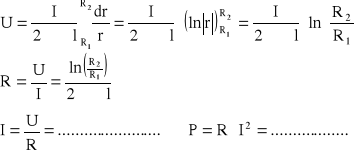
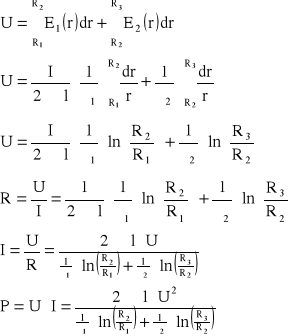
Zad4. Kondensator cylindryczny uwarstwiony szeregowo dwoma dielektrykami o R1, R2, R3, długości l i kond1 i kond2. Obliczyć: R, I, P.
![]()
Zad5. Półkolisty uziom o promieniu R zakopano w ziemi. Obliczyć napięcie krokowe UK od środka uziomu. Długość kroku wynosi k Dane R-promień, r-odległość, I-prąd, konduktywność
![]()
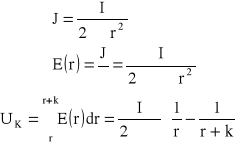
Zad6. Przez uziom w postaci kuli metalowej stanowiącej uziemienie silnika, w wyniku uszkodzenia izolacji silnika płynie prąd stały I. Obliczyć napięcie krokowe między punktami odległymi od środka kuli o R1 o R2. Konduktywność gruntu znana.
Analiza pola magnetycznego:
Równania Maxwella:
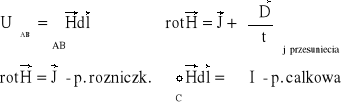
Cyrkulacja wektora H natężenia pola magnetycznego po krzywej C jest równa sumie prądów.
Zad1. Obliczyć rozkład natężenia pola magnetycznego H wewn i na zewn długiego przewodu prostoliniowego o przekroju kołowym, którego promień wynosi R, przez który płynie prąd stały I.
![]()
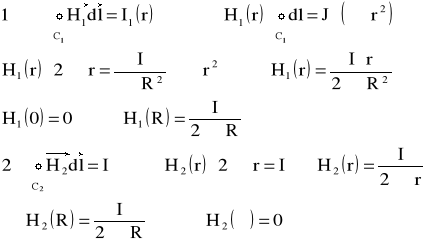
Zad2. Wyznaczyć rozkład natężenia pola magnetycznego H(r) w płaszczyźnie poprzecznego przekroju prostoliniowego rurowego przewodu o R1 i R2 przez który płynie prąd stały I.
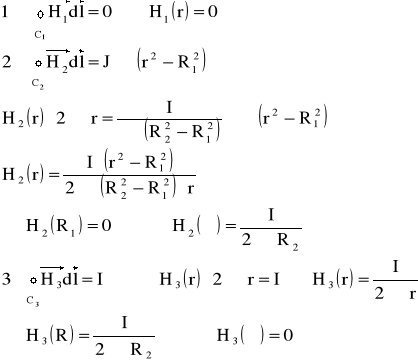
Zad3. Prosty długi przewód rurowy przez który płynie prąd stały I2 oraz przewód pełny o przekroju kołowym przez który płynie prąd I1 umieszczono współśrodkowo. Wyznaczyć rozkład natężenia pola magnetycznego H(r) w płaszczyźnie przekroju poprzecznego. Dane: R1, R2, R3, I1, I2 (I1 > I2)
![]()
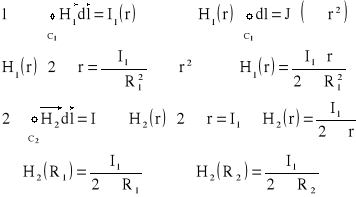
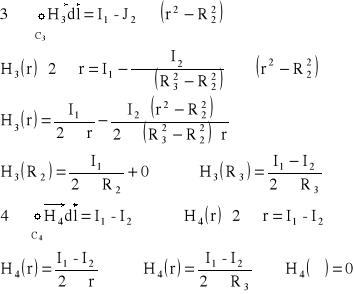
Zad4. Obliczyć i narysować rozkład natężenia pola elektrycznego linii dwuprzewodowej przy przeciwnym kierunku prądów. Dane: I-prąd, d-odległość między osiami przewodów, R-promień przewodów.
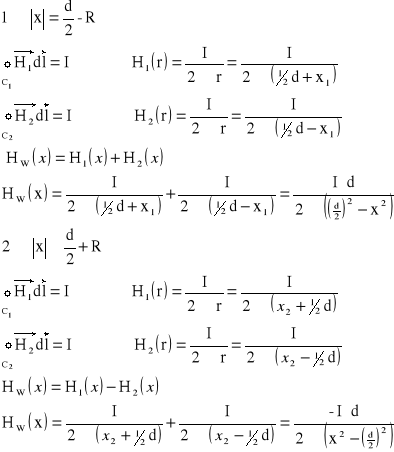
Strumień magnetyczny i indukcyjność własna:
Zad1. Obliczyć strumień magnetyczny przenikający przez powierzchnię między dwoma równoległymi przewodami, gdy odległość między nimi wynosi l, a przenikalność magnetyczna ośrodka - μ0. Obliczyć indukcyjność linii dwuprzewodowej.
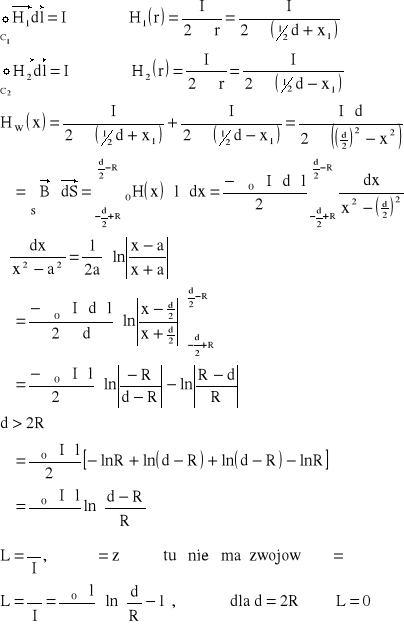
![]()
Zad2. Obliczyć indukcyjność własną kabla koncentrycznego o długości l, pomijając wymiary poprzeczne płaszcza oraz przewodu wewnętrznego. Dane: R1, R2, l.
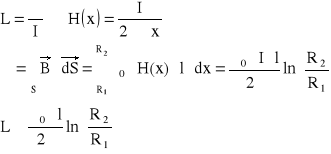
Zad3. Obliczyć indukcyjność własną linii dwuprzepustowej. Przewody są równoległe a odległości między osiami wynoszą d, długość przewodów l i promień przewodów R.
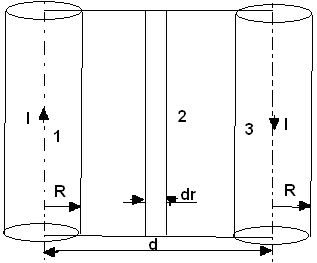
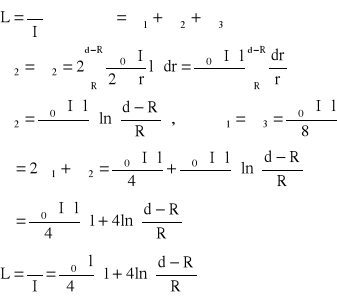
Energia i indukcyjność własna:
Zad1. Obliczyć indukcyjność własną przewodu walcowego o promieniu R i długości l oraz obliczyć energię pola magnet. zawartego w tym przewodzie:
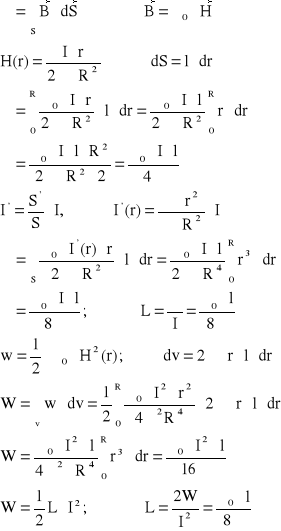
Indukcyjność wzajemna:
Zad1. Długa 2 przewodowa linia i prostokątna ramka zawierająca z zwojów z bardzo cienkiego drutu umieszczone są w jednej płaszczyźnie. Obliczyć indukcyjność wzajemną tych dwóch obwodów.
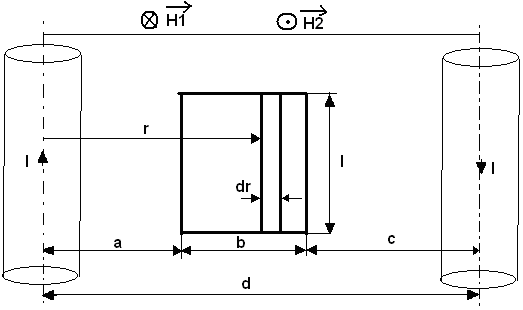
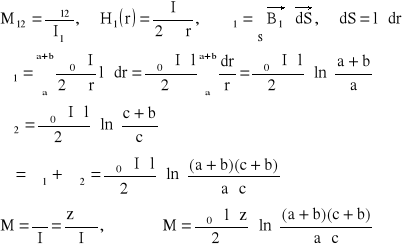
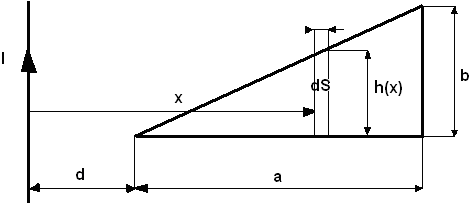
Zad2. Długi prosty przewód oraz ramka o kształcie trójkąta prostokątnego zawierającego z zwojów umieszczone są w jednej płaszczyźnie. Obliczyć indukcyjność wzajemną tych obwodów.
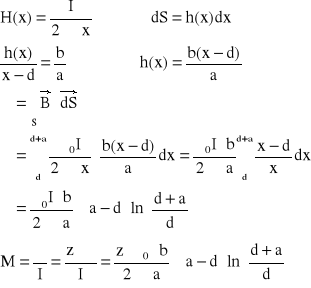
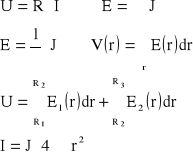
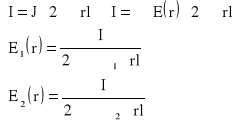
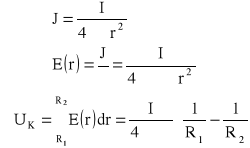
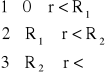
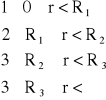
Wyszukiwarka
Podobne podstrony:
ELEKTRA kOLO, NAUKA, studia, elektra
ściąga-elektra, NAUKA, studia, elektra wykład, word
sciaga z pozostalych pytan - elektra, NAUKA, studia, elektra wykład, word
Sprawozdanie z ćwiczenia nr 2(transformator), Studia, AAAASEMIII, 3. semestr, Elektrotechnika II, Pa
Ściąga-Fizyka ED 7, Politechnika Lubelska, Studia, Studia, sem VI, z ksero na wydziale elektrycznym
KOLO - Sciaga1, Elektrotechnika I stopień PWSZ Leszno, SEMESTR III, inżyneria materiałowa, ściagi
Obwód szeregowy RLC w stanie nieustalonym, NAUKA, studia, lab elektrotechnika, RLC
elektra 2007max, NAUKA, studia, elektra wykład, word
sprawko - quickfield - moje, NAUKA, studia, lab elektrotechnika
Ściąga-Zabezpieczenia Rutka D, Politechnika Lubelska, Studia, Studia, sem VI, z ksero na wydziale el
sciaga 3 i 4, elektrotechnika cwiczenia
elektra, NAUKA, studia, elektra
ściąga z elektry, Przwatne, Studia, elektrotechnika laborki
tium sciaga, Elektronika i telekomunikacja-studia, rok III, sem V, tium
sciaga-elektrotechnika, Studia, [xxx] Rok I, Elektrotechnika, Download
Stery sciaga, Elektrotechnika PP, 3 Semestr, Automatyka, Kolo kwapisz i florek, Automatyka, automaty
Ściąga-Teoria sterowania, Politechnika Lubelska, Studia, Studia, sem VI, z ksero na wydziale elektry
sciaga 2 i 5, elektrotechnika cwiczenia
sprawko z 5 z elektry, NAUKA, studia, lab elektrotechnika
więcej podobnych podstron